2015-06-28
1052Рассмотрим конечную игру двух лиц с нулевой суммой. Пусть игрок 1 имеет т ходов —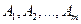 
,а игрок 2 (противник) -— п ходов 
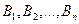. Если игрок 1 выбрал ход 
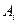, игрок 2 выбрал 
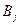,то они получают выигрыш, соответственно: 
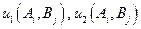причем 
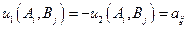Из элементов 
можно составить матрицу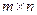 
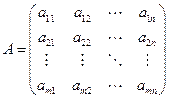
которая называется платежной- Тогда ходу 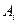игрока 1 будет соответствовать выбор им 
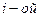строки матрицы А, а ходу 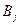для игрока 2— 
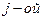столбца. Цель игрока 1 максимизировать 
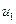игрока 2 — максимизировать 
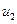(или минимизировать 
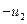). Игроки выбирают свои ходы не зная какие ходы выберет противник. Считая противника разумным, игроки могут придерживаться осторожных (перестраховочных) стратегий. Игрок 1 в каждой строке находит минимальный элемент 
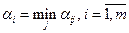, а затем находит свой гарантированный выигрыш 
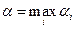. Выбор соответствующий строки (строк) будет его макси-минной стратегией (при любом поведении игрока 2 он получит не менее 
). Аналогично игрок 2 находит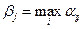 
и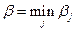 
. Его мини-максной стратегией будет выбор соответствующего столбца (при любом поведении игрока а он обеспечит себепроигрыш не более 
).
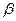Если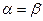 
, то это значит, что существует элемент 
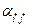который будет минимальным в строке 
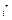и максимальным в столбце 
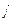. Тогда стратеги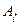и 
и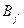 
будут оптимальными для игроков 1 и 2. Величина 
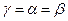называется ценой игры, а пара ходов (
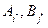) — седловой точкой игры.
Если седловой точки у игры нет и розыгрыши совершаются неоднократно, то естественно для игрока 1 попытаться увеличить а, а для игрока 2 — уменьшить .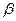
Смешанными стратегиями игроков 1 и 2 будем называть соответственно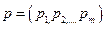 
и 
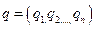, где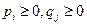 
— вероятности (частоты) применения чистых стратеги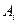й и 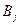при этом 
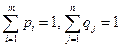.Величина 
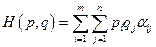— средний выигрыш (математическое ожидание игрока 1).
Основная теорема. Любая матричная игра имеет пару оптимальных смешанных стратегий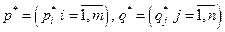 
, обладающую свойством:
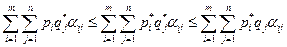
и цену игры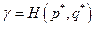 
. (То есть если игрок 1 не придерживается р*, а игрок 2 придерживается q* тогда он может получить меньше 
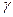. Соответственно для игрока 2.)
Будем считать.что все элементы платежной матрицы неотрицательны (если это не так, то можно ко всем ее элементам прибавить некоторое положительное число L, переводящее платежи в область неотрицательных значений; при этом решение игры р* и q* не изменится, цена игры лишь увеличится на L. Тогда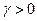 
Введем обозначения: 
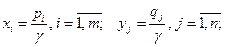
Известно, что задача нахождения р* и q* сводится к паре взаимодвойственных задач:
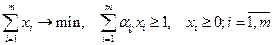(1)
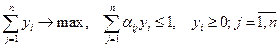(2)
Предположим, что мы нашли их решения (оно всегда существует)
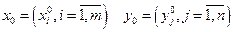
Тогда:
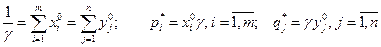
Замечание. Задачу (2) удобно решать, применяя симплекс-метод, а задачу (1) — двойственный симплекс-метод. Однако на практике достаточно решить лишь одну из них, например задачу (2). Решение двойственной ей задачи (1) легко получить из последней симплекс-таблицы (см. пример).
Оптимальные стратегии р* и q* можно искать, применяя приближенный метод Брауна-Робинсон, который заключается в следующем. Розыгрыш осуществляется искусственно. Игроки попеременно выбирают свои стратегии (строки и столбцы матрицы А), в ответ на поведение противника. Этот выбор они делают по результатам всех предыдущих ходов. Суммируются выбранные ранее строки игроком 1 и столбцы игроком 2. После чего игрок 2 находит минимальное число в полученной строке и отвечает соответствующей ему стратегией, а игрок 1 находит максимальное в полученном столбце и делает соответствующий ему ход. Начинает розыгрыш, например, игрок 1 стратегией А1. Данные сводятся в специальную таблицу (смотри пример). Там же записываются средний выигрыш а игрока 1 и средний проигрыш 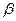игрока 2. После достаточного количества итераций (N), подсчитывают частоты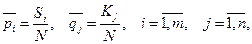 
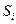— количество стратегий Ai; в них; Kj — количество стратегий Bj в них. Они и служат приближенными значениями для р* и q*. Средние арифметические а и 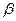, служат оценками нижней и верхней цены игры. Известно, что при 
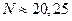может быть получено достаточно хорошее приближение к решению задачи. Пример. Решить игру, заданную следующей платежной матрицей
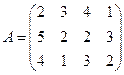
Решение.
1. Прежде всего проверим не имеет ли матрица А седловой точки:
.
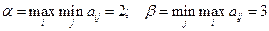Так как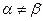 
, то седловой точки нет и решением игры будет смешанная стратегия, а цена игры заключена в пределах 2 < v < 3.
2. Решим игру сведением к задаче линейного программирования. Для этого построим пару взаимодвойственных задач по матрице А:
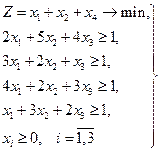(1) 
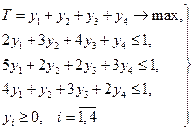(2)
Решим, например, вторую задачу. Чтобы решить эту задачу симплекс-методом, приведем ее к каноническому виду.
Построим симплекс-таблицы:
| С | 1 1 1 1 0 0 0 | |||
| СБ | аБ | b | a1 a2 a3 a4 a5 a6 a7 |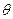 
|
| a5 a6 a7 | 2 3 4 1 1 0 0 5 2 2 3 0 1 0 4 1 3 2 0 0 1 | 1/2 1/5 1/4 | ||
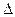
| -1 -1 -1 -1 0 0 0 | |||
| a5 a1 a7 | 3/5 1/5 1/5 | 0 11/5 16/5 -1/5 1 -2/5 0 1 2/5 2/5 3/5 0 1/5 0 0 -3/5 7/5 -2/5 0 1/5 1 | 3/11 1/2 --- | |
|
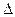
| 1/5 | 0 -3/5 -3/5 -2/5 0 1/5 0 | ||
| a2 a1 a7 | 3/11 1/11 4/11 | 0 1 16/11 -1/11 5/11 -2/11 0 1 0 -2/11 7/11 -2/11 3/11 0 0 0 25/11 -5/11 3/11 1/11 1 | ||
|
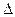
| 4/11 | 0 0 3/11 -5/11 3/11 1/11 0 | ||
| a2 a4 a7 | 2/7 1/7 3/7 | |||
|
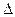
| 3/7 | 5/7 0 1/7 0 1/7 2/7 0 |
Оптимальное решение задачи (2):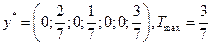 
|. Получим цену игры 
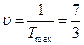и компоненты оптимальной смешанной стратегии 
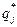игрока B:
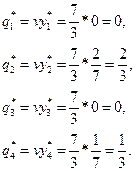
Так как базисным переменным у5, у6, у7 задачи (2) соответствуют свободные переменные хъх2,х3 задачи (1), можем из 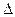-строки последней симплекс-таблицы выписать оптимальное решение задачи (1):
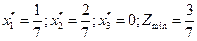
Теперь вычислим компоненты оптимального оптимальной смешанной стратегии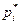 
игрока А:
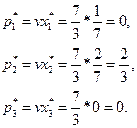
Итак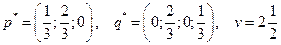 
.
3. Решим игру методом Брауна-Робинсона. Чтобы получить неплохое приближенное решение игры этим методом вам достаточно выполнить 20 итераций.
Вычисления удобно проводить в следующей таблице (см. таблицу 1)
Первый свой ход игрок А выбирает случайным образом, например, стратегию А1. В столбцы В1-В4 при первой итерации записывается строка исходной матрицы, соответствующая выбранной стратегии игрока 1, а затем суммируются строки, согласно выбранным в последствии стратегиям этот игрока. В столбцах А1-А3 заносятся суммы столбцов матрицы А соответственно выбранным ходам игрока 2. Стратегии (столбцы и строки) игроки 2 и 1 выбирают попеременно, в ответ на ход противника и так, чтобы минимизировать свой проигрыш (выбирается наименьшее число среди A1-An)и максимизировать свой выигрыш (выбирается среди В1-В3), соответственно.
Каждый раз рассчитываются:
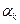— наименьший из накопленных выигрышей игрока 1 за k партий, деленный на число партий k;
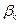— наибольший из накопленных проигрышей игрока 2 за k партий, деленный на число партий k:
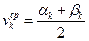— приближенное значение цены игры.
Сделав последнюю итерацию, определяем вероятности применения игроками своих стратегий:
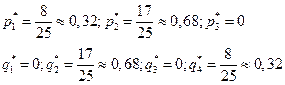
Приближенное значение цены игры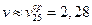 
.
Сравнив это решение с полученным в предыдущем пункте видим, что получились очень близкие значения.
Задание: решить матричную игру сведением к задаче линейного программирования и методом Брауна-Робинсона, сравнить ответы.
Таблица 1.
| Номер партии | Игрок 1 | Игрок 2 | Приблизительное значение цены игры | |||||||||
| Стратегия игрока 1 | Накопленный выигрыш при стратегиях игрока 2 | Стратегия игрока 2 | Накопленный выигрыш при стратегиях игрока 2 |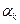
|
| 
| ||||||
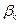
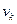
| B1 | B2 | B3 | B4 | A1 | A2 | A3 | ||||||
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. | A1 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A2 A1 A1 A1 A1 A1 A1 A1 | B4 B4 B4 B4 B4 B4 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B2 B4 B4 | 1,5 1,8 2,14 2,13 2,11 2,1 2,1 2,08 2,08 2,07 2,07 2,06 2,06 2,06 2,11 2,15 2,19 2,23 2,26 2,25 2,2 | 2,86 2,75 2,67 2,6 2,55 2,5 2,46 2,43 2,4 2,38 2,35 2,33 2,37 2,4 2,43 2,45 2,48 2,42 2,36 | 2,5 2,25 2,4 2,5 2,5 2,44 2,39 2,35 2,32 2,29 2,27 2,25 2,24 2,22 2,21 2,2 2,34 2,26 2,31 2,34 2,37 2,33 2,28 |
