2015-07-14
17263ЧАСТЬ 2. ТЕПЛОМАССООБМЕН Тема 9. ТЕПЛОПРОВОДНОСТЬ
9.1.Основные понятия и определения
Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.
Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.
Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).
Конвекция осуществляется путем перемещения в пространстве неравномерно нагретых объемов среды. При этом перенос теплоты неразрывно связан с переносом самой среды.
Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.
Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.
|
|
|
Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.
Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.
Совместное протекание процессов теплообмена и массообменна называется тепломассообменном.
Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.
Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:
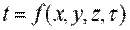(9.1)
где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда
, 
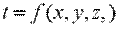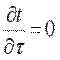(9.2)
Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:
|
|
|
; 
; 
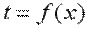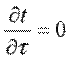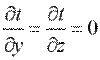
Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной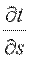 
, принимающей наибольшее значение в направлении нормали к изотермической поверхности 
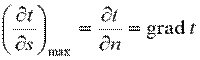(9.3)
Вектор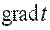 
называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.
9.2.Закон Фурье
Согласно гипотезе Фурье, количество теплоты d2Qτ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту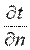 
: 
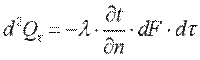(9.4)
Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:
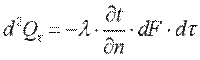(9.5)
Проекции вектора q на координатные оси соответственно:
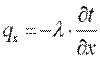
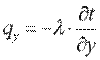
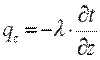
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком: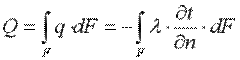 
(9.6)
Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения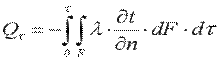 
(9.7)
9.3.Коэффициент теплопроводности
Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):
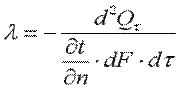(9.8)
Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции
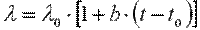(9.9)
где λ0 — значение коэффициента теплопроводности при температуре t0=0 0С; b — постоянная, определяемая опытным путем.
Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 0С равен 0,0244 Вт/(м·К).
Для жидкости λ =0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 0С и дальше уменьшается.
Наилучшими проводниками теплоты являются металлы, у которых λ =20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.
|
|
|
Материалы с λ <0,25 Вт/(м·К), обычно применяемые для тепловой изоляции, называют теплоизоляционными. Большинство теплоизоляционных и строительных неметаллических материалов имеют пористое строение, что не позволяет рассматривать их как сплошную среду.
9.4.Дифференциальное уравнение теплопроводности в плоской стенке при граничных условиях первого рода
9.4.1.Дифференциальное уравнение теплопроводности
Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, воспользуемся методом математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.
При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с (теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной qv — количеством теплоты, которое выделяется в единице объема в единицу времени.
В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQвн и внесенная извне в элементарный объем путем теплопроводности dQm за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:
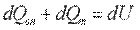(9.10)
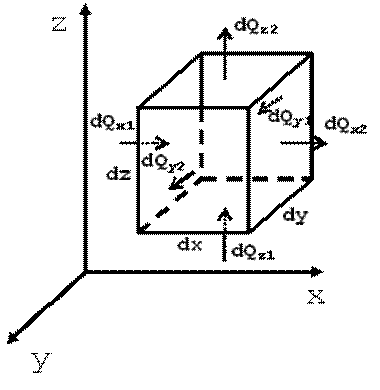
Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 9.1). Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ: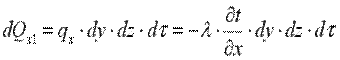 
|
|
|
|
| Рис. 9.1. К выводу дифференциального уравнения теплопроводности |
На противоположной грани параллелепипеда температура получит приращение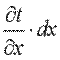 
и будет составлять 
.
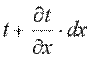Количество тепла, отведенного через эту грань: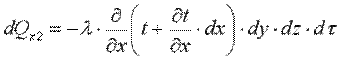 
Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси ОX: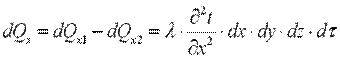 
Аналогично: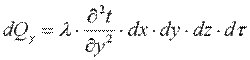 
Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности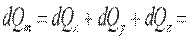 
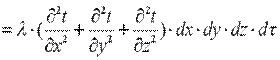
Здесь произведение dx·dy·dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников: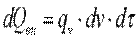 
Приращение внутренней энергии можно выразить через массу параллелепипеда ρ·dv, теплоемкость с и приращение температуры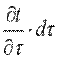 
: 
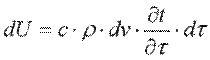
Подставляя выражения для dQm, dQвн и dU в уравнение (9.10), после соответствующих сокращений получаем:
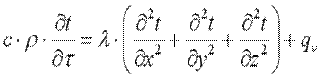(9.11)
Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом: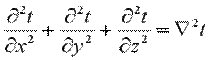 
Величину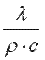 
называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид:
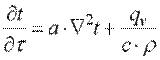(9.12)
Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.
9.4.2.Краевые условия
Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.
Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает процесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:
1) первого рода, задается распределение температуры на поверхности тела в функции времени;
2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;
3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана: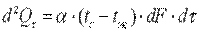 
(9.13)
где tc — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,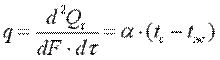 
(9.14)
Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности: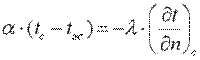 
Переписав последнее уравнение в виде:
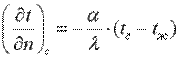(9.15)
получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.
9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода
|
| Рис. 9.2. Однородная плоская стенка |
Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры tс1 и tс2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме (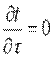
) и отсутствии внутренних источников теплоты (qv =0) дифференциальное уравнение теплопроводности примет вид: 
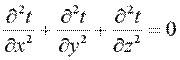(9.16)
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае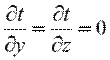 
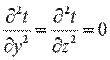и дифференциальное уравнение теплопроводности перепишется в виде:
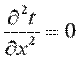(9.17) Граничные условия первого рода запишутся следующим образом: при x=0 t=tc1; при x=δ t=tc2. Интегрируя уравнение (9.17), находим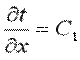 
После второго интегрирования получаем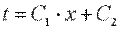 
(9.18)
Постоянные С1 и С2 определим из граничных условий: при x=0 t=tc1, С2=tc1; при x=δ t=tc2=С1·δ+tc1, отсюда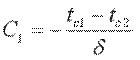 
. Подставляя значения С1 и С2 в уравнение (9.18), получим уравнение распределения температуры по толщине стенки: 
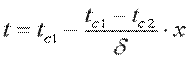(9.19)
Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому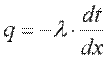 
.
Учитывая, что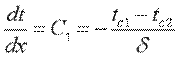 
, получим 
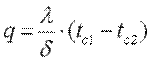(9.20)
Общее количество теплоты, которое передается через поверхность стенки F за время τ,
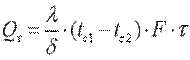(9.21) Отношение 
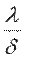называют тепловой проводимостью стенки, обратную ей величину 
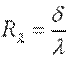- термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λс, взятый при средней температуре стенки.
ТЕПЛОВОЙ ПОТОК — количество теплоты, переданное через изотермическую поверхность в единицу времени.
Т.П.количество теплоты, переданное через изотермическую поверхность в единицу времени. РазмерностьТ. п. совпадает с размерностью мощности (См. Мощность). Т. п. измеряется в Ваттахили ккал / ч (1 вт = 0,86 ккал / ч).Т. п., отнесённый к единице изотермической поверхности, называется плотностью Т. п., удельным Т.п. или тепловой нагрузкой; обозначается обычно q, измеряется в вт / м 2 или ккал / (м 2 ․ч). Плотность Т. п. —вектор, любая компонента которого численно равна количеству теплоты, передаваемой в единицу временичерез единицу площади, перпендикулярной к направлению взятой компоненты.
Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания)температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянномдавлении, в системе СИ измеряется в м²/с.
,
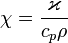где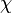 
— температуропроводность, 
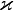— теплопроводность, 
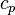— изобарная удельная теплоёмкость, ρ — плотность
Температуропроводность и теплопроводность являются двумя из наиболее важных параметров веществ и материалов, поскольку они описывают процесс переноса теплоты и изменение температуры в них.
Величина коэффициента температуропроводности зависит от природы вещества. Жидкости и газы обладают сравнительно малой температуропроводностью. Металлы, напротив, имеют бо́льший коэффициент температуропроводности.
Коэффициент температуропроводности в тепловых процессах характеризует скорость изменения температуры. [ 2 ]
Коэффициент температуропроводности (а) - служит мерой скорости, с которой пористая среда передает изменение температуры с одной точки в другую. [ 3 ]
Коэффициент температуропроводности характеризует скорость выравнивания температуры (тепловую инертность) тела и по аналогии с коэффициентом диффузии, с которым он имеет одинаковую размерность, иногда называется коэффициентом тепловой диффузии. [ 4 ]
Вывод уравнения теплопроводности:
Рассмотрим задачу о распространении тепла в неревномерно нагретом твердом теле. В качестве величины,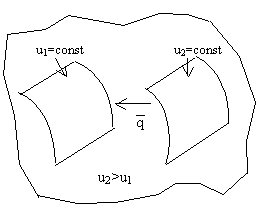 
характеризующей процесс, возьмем температуру u (M,t), где M = M (x,y,z) - некоторая точка внутри рассматриваемого тела.
Посмотреть определения потока и дивергенции векторного поля
1) Будем рассматривать процесс распространения тепла посредством теплопроводности (т.е. при непосредственном контакте областей с разной температурой).
2) Для теплообмена посредством теплопроводности необходимо наличие ненулевого температурного градиента, т.е. различные части тела должны иметь разную температуру. При этом, так как каждая система стремится к своему равновесному состоянию, происходит переток тепла от более "нагретых" частей тела к более "холодным".
3) Для математического описания полей тепловых потоков введем в рассмотрение вектор плотности теплового потока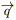 
, имеющий направление от более "горячих" участков тела к более "холодным", а по величине равный количеству тепла, проходящему через единицу поверхности за единицу времени: 
.
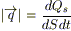4) В основе аналитической теории теплопроводности лежит экспериментально установленный закон Фурье, согласно которому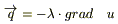 
, где λ - коэффицент теплопроводности среды (равен количеству тепла, переносимого в единицу времени через единицу поверхности при градиенте температуры, равном единице).
5) Будем считать, что наше изучаемое тело изотропно, т.е. λ = λ (x,y,z) и не зависит от выбора нормали к поверхности;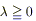 
.
6) По определению потока для вектора 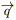можем записать 
.
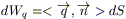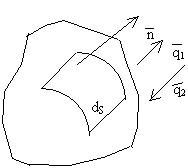При этом получим: если тело отдает тепло, то 
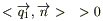; если получает, то 
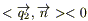. Условимся в дальнейшем для определенности считать поток тепла dQs, направленный внутрь тепла положительным. Для этого в определение потока введем знак "-" (минус). Тогда элементарный поток через поверхность dS за время dt: 
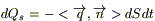, и через всю поверхность S, ограничивающую объем S за время 
.
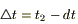(1) 
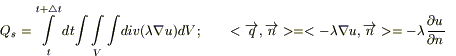
7) Предположим, что внутри нашего объема есть источники тепла. Обозначим через F (M,t) - плотность тепловых источников (количество тепла, выделяемое в единице объема за единицу времени). Тогда во всем объеме V за время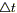 
выделится QV количества тепла: [для элементарного объема dV выделяемое количество тепла dQV = F (M,t) dVdt ]:
(2) 
.
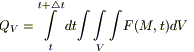8) В соответствии с 1м началом термодинамики тепло, получаемое системой идет на изменение ее температуры и на совершение этой системой работы: Q = Cdu + δA. Будем считать, что δA = 0 (для твердых тел).
du - изменение температуры за время 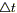в точке М: 
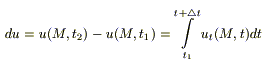(по теореме о конечных приращениях).
C - теплоемкость объема V, может быть расписана через удельную теплоемкость с, плотность вещества p и объем V: C dV = c (M)r(M)dV - для элементарного объема dV. Тогда
(3) 
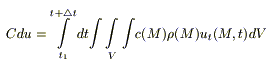- для объема V.
В наш выделенный объем тепло δQ поступает за счет 2x механизмов: переноса тепла через поверхность, и возникновения тепла за счет работы источников).
Q = Qs+ QV; т.е. Cdu = Qs+ QV.
Подставим (1), (2), (3):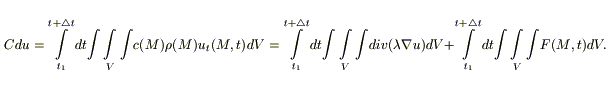 
Применим теорему о среднем значении (дважды: по t и по V) к каждому из этих интегралов:
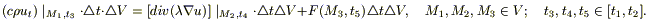
Поделим полученное соотношение на (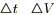
) и перейдем к пределу при 
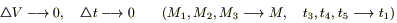, так как t1 - любое время (могли вместо t1 и t2 взять t и 
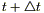); получим уравнение, описывающее изменение температуры в любой точке М в любое время t.
(1) 
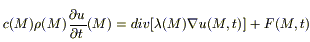или
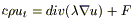- уравнение теплопроводности.
Если среда однородна, то λ,c,p - const и λ можно вынести из под функции div,и, поделив на (cp), получим:
(1a)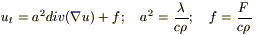 
, так как 
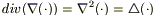, то
(1б)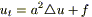 
- уравнение теплопроводности для однородной среды.
Если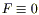 
, то уравнение будет однородным.
Рассмотрим теперь дополнительные условия, необходимые для однозначного решения задачи:
а) Необходимо знать начальное распределение температуры:
(2) u (M,0) = φ (M);
б) Тепловой режим на границе. Основные виды тепловых режимов:
I. - на границе поддерживается определенная температура
II. - через границу подается определенный тепловой поток
III. - происходит теплообмен с внешней средой, температура которой известна.
Разберем более подробно каждый из типов:
I. (3а) u/s = f 1(P,t), где f 1 - известная функция, P є S; если поддерживается нулевая температура, то u/s = 0.
II. Обозначим через ν (P,t) - плотность теплового потока на границе S. (Количество тепла, проходящего через единицу площади за единицу времени).
Пусть σ - произвольный участок поверхности S, ограниченный замкнутой гладкой кривой.
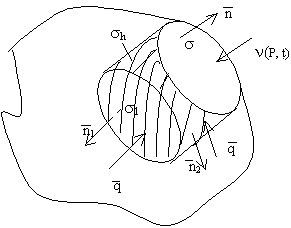Рассмотрим объем V в виде прямого цилиндра с основанием σ и высотой h; второе основание - σ 1 - есть поверхность параллельная σ (
).
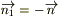Для записи 1го начала термодинамики (закон сохранении энергии):
Cdn = dQ;
;
;
;
.
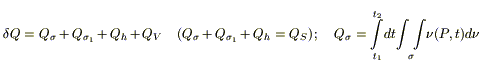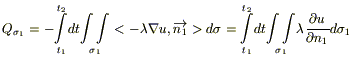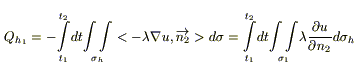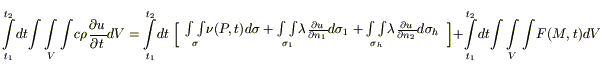при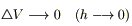 
интегралы по V, а также интеграл по 
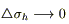, при этом так как 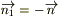и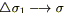 
.
Применяя дважды теорему о среднем (по t и по σ), устремляя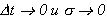 
, получаем:
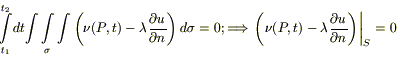
(3б)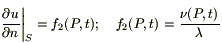 
Если поверхность S теплоизолирована (ν = 0):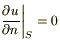 
III. Будем считать, что теплообмен между телом и окружающей средой происходит по закону Ньютона: плотность теплового потока ν (P,t), получаемого из внешней среды, пропорциональна разности температуры окружающей среды θ (t) и температуры u внутри V вблизи поверхности S.
(*) ν (P,t) = H (θ (t) - u (P,t)) P є S (H - коэффициент теплообмена).
Таким образом, мы имеем случай II, где ν (P,t) имеем специфический вид (*), т.е.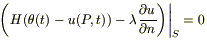 
;
(3в)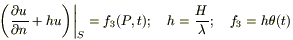 
.
В случае, если температура окружающей среды θ (t) = 0, получим однородное граничное условие 3города: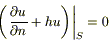 
.
Таким образом, мы приходим к задаче: найти решение уравнения теплопроводности (1), удовлетворяющее нормальным условиям (2) и одному из граничных условий (3). Совершенно аналогично ставятся задачи в одномерном и двумерном случаях. Для уравнения (1) можно также поставить задачу Коши (т.е. задачу без граничных условий)
Замечание: к уравнению (1) приводятся и другие физические задачи: уравнение диффузии, движение вязкой жидкости.
2.1. Метод разделения переменных для конечного стержня
http://de.ifmo.ru/--books/0051/index.html
http://de.ifmo.ru/--books/0051/2/2_1/21yrteplmetraz_1.htm
Уравнение теплопроводности относится к уравнениям параболического типа.
Уравнение теплопроводности имеет вид:
,
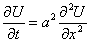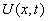- температура стержня в точке 
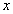в момент времени 
,
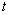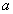- связано с коэффициентами теплоемкости и теплопроводности.
Рассмотрим однородный стержень длины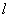 
, теплоизолированный с боков и достаточно тонкий, чтобы в любой момент времени температуру во всех точках поперечного сечения можно было считать одинаковой (см. рисунок 1).
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия. Для задач этого типа задается только одно начальное условие, а именно, начальная температура в начальный момент времени. Итак,
 .
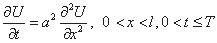| (1) |
Краевые условия:
 ,
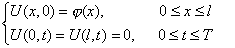| (2) (3) |
где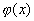 
-начальное распределение температуры в стержне.
Концы стержня закреплены в термостате. В данном случае тепловая энергя стержня не сохраняется, так как система не является изолированной.
Будем искать решение в виде произведения двух функций
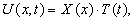
где X (x)- функция только переменного x,
а T (t)- функция только переменного t.
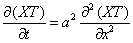
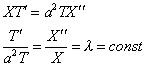
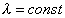, так как левая часть равенства зависит только от t, а правая – только от x. Отсюда следует, что
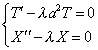
Граничные условия (3) дают:
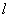X (0)=0, X ()=0,
тогда
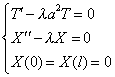
| (4) (5) (6) |
Необходимо определить знак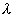 
.
1 случай: Пусть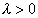 
.
Рассмотрим уравнение (4):
.
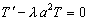Характеристическое уравнение имеет вид:
.
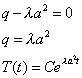Рассмотрим уравнение (5):
.
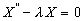Характеристическое уравнение имеет вид:
 .
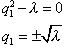
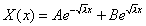| (7) |
Это решение не подходит, так как если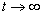 
,то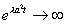 
, а поэтому нарушается второй закон термодинамики, то есть происходит передача энергии от холодного к горячему. Докажем это математически, подставив начальные условия (6) в (7):
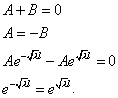
Значит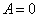 
или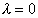 
, но тогда мы получаем тривиальное решение и не можем удовлетворить начальным условиям. Следовательно, при 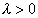уравнение (1) имеет только нулевое решение.
2 случай: Пусть 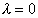, тогда
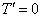, следовательно, 
.
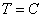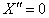, следовательно, 
.
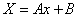Подставим краевые условия
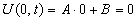, получим 
.
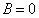В итоге получим нулевое решение 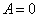, а значит 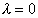не подходит.
3 случай: Пусть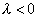 
и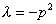 
, тогда
.
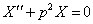Характеристическое уравнение имеет вид:
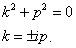
Общее решение может быть записано в виде:
 .
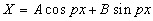| (8) |
Подставим краевые условия.
.
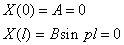Получаем
 .
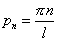| (9) |
Существуют нетривиальные решения уравнения (5), равные
 .
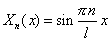| (10) |
Этим значениям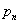 
соответствуют решения уравнения (4)
,
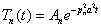где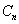 
- неопределенный пока коэффициент.
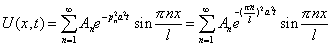
| - общее решение. |
Удовлетворим начальным условиям (2):
.
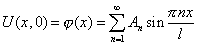Для выполнения этого начального условия необходимо взять в качестве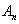 
коэффициент Фурье:
.
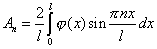Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.
Уравнение теплопроводности для бесконечного стержня
Рассмотрим задачу с начальными данными на бесконечной прямой. А именно, найдем ограниченную функцию, 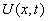определенную в области 
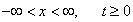, удовлетворяющую уравнению теплопроводности
|
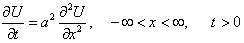
и начальному условию
|
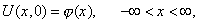
где функция 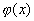задает начальное распределение температуры.
Сделаем преобразование Фурье по переменной 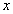от уравнения и начального условия
.
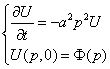
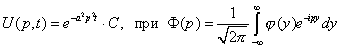
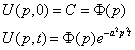Чтобы получить итоговое решение, нужно провести обратное преобразование Фурье
.
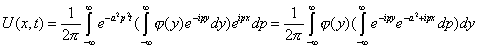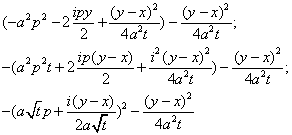
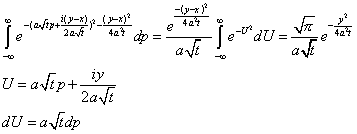
Тогда общее решение имеет вид
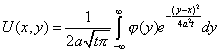
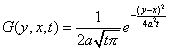
| - функция Грина для уравнения теплопроводности. |
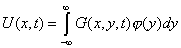
| - общее решение (стандартный вид). |
Эта функция дает решение уравнения теплопроводности с заданным начальным условием.
http://www.apmath.spbu.ru/ru/education/final/question22.pdf
http://pskgu.ru/ebooks/kgs/kgs_gl28_02.pdf
http://main.isuct.ru/files/publ/PUBL_ALL/0154.pdf
https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8
!!!
http://edu.sernam.ru/lect_gam.php?id=32
