Содержание

1. Тождественные частицы……………...………………………………… 3

2. Состояния с n бозе-частицами ……...………………………………….. 6

3. Принцип запрета………………………………... …………….………... 8

4. Обменное взаимодействие…………….………………………………... 9

5. Список литературы………………………………………………………11

ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ

Тождественные частицы - это такие частицы, которые, подобно электронам, никак невозможно отличить друг от друга.

Представим, что сталкиваются две частицы а и b и частица а рассеивается в направлении 1, а частица Ь— в направлении 2 (фиг. 2.1, а). Пусть f(Θ) будет амплитуда этого процесса; тогда вероятность Р1 наблюдения подобного события пропорциональна квадрату аплитуды f(θ)|. Конечно, могло случиться, что частица b рассеялась в счетчик 1, а частица а направилась в счетчик 2 (фиг. 2.1, б). Если считать, что никаких специальных направлений, определяемых спином или чем-нибудь подобным, в опыте нет, то вероятность Р2 этого события можно просто записать в виде |f(π—θ)|^2, потому что этот процесс попросту эквивалентен первому процессу, в котором счетчик 1 поставили под углом (π—Θ). И вам могло бы показаться, что амплитуда второго процесса равна просто f(π—Θ). Но это не обязательно так, потому что в ней мог стоять произвольный фазовый множитель. Иначе говоря, амплитуда могла бы быть такой:

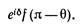
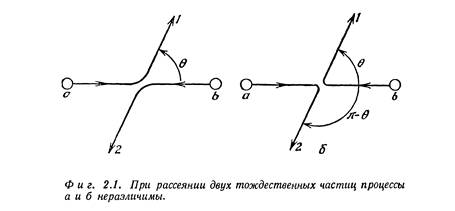
Посмотрим теперь, что случается, если частицы а и Ь оказываются идентичными. Тогда два разных процесса, показанных на двух частях фиг. 2.1, уже нельзя друг от друга отличить. Существует амплитуда того, что а или b попадает в счетчик 1, тогда как оставшаяся частица попадает в счетчик 2. Эта амплитуда есть сумма амплитуд двух процессов, показанных на фиг. 2.1.

первую мы обозначим f(Θ), а вторая будет 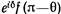. и теперь уже фазовый множитель очень важен, потому что мы собираемся складывать амплитуды. Предположим, что мы обязаны умножать амплитуду на некий фазовый множитель всякий раз, когда две частицы обмениваются ролями. Если они еще раз обменяются ими, то множитель появится еще раз. Но при этом мы снова возвратимся к первому процессу. Фазовый множитель, взятый дважды, должен вернуть нас к тому, с чего мы начали,— его квадрат должен быть равен единице. Есть только две возможности: ет равно либо +1, либо —1. Обмен приводит ко вкладу в амплитуду с тем же знаком или ко вкладу с противоположным знаком. И оба случая встречаются в природе, каждый для своего класса частиц. Частицы, интерферирующие с положительным знаком, называются бозе-частицами, а те, которые интерферируют с отрицательным знаком, именуются ферми-частицами.

Стало быть, амплитуда рассеяния тождественных частиц имеет вид

для бозе-частиц: (Амплитуда процесса) + (Амплитуда обмена)

Для двух частиц амплитуда рассеяния запишется в форме

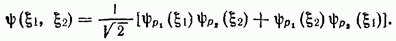
В общем же случае системы произвольного числа частиц N нормированная волновая функция

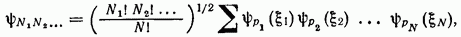
для ферми-частиц: (Амплитуда процесса) — (Амплитуда обмена)

Для системы фермионов волновая функция есть антисимметричная комбинация произведений (61,1). Так, для системы из двух частиц имеем

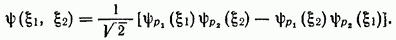
В общем же случае N частиц волновая функция системы записывается в виде определителя

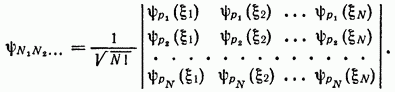
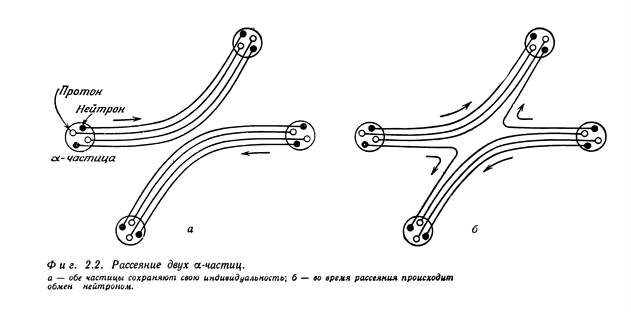
Интересная проблема возникает при наличии двух или больше тесно связанных частиц. К примеру, в α-частице сидят четыре частицы: два нейтрона и два протона. И когда рассеиваются две α-частицы, может представиться несколько возможностей. Может случиться, что при рассеянии обнаружится конечная амплитуда того, что один из нейтронов перескочит от одной α-частицы к другой, а нейтрон из другой α-частицы перейдет к первой, так что две α-частицы после рассеяния оказываются не первоначальными частицами — произошел обмен парой нейтронов (фиг. 2.2). Амплитуда рассеяния с обменом парой нейтронов будет интерферировать с амплитудой рассеяния без такого обмена, и интерференция должна иметь знак минус, потому что состоялся обмен ферми-частицами. С другой стороны, если относительная энергия двух α-частиц так мала, что они находятся сравнительно далеко друг от друга (скажем, из-за кулоновского отталкивания) и вероятность обмена любыми внутренними частицами оказывается незначительной, в этом случае α-частицу можно считать простейшим объектом, не задумываясь о деталях ее внутреннего строения. В этих условиях в амплитуду рассеяния войдут только два члена.

Либо обмена вовсе нет, либо при рассеянии происходит обмен всеми четырьмя нуклонами. Поскольку и протоны, и нейтроны в α-частице — это ферми-частицы, обмен любой парой меняет

знак амплитуды рассеяния. Пока внутри α-частиц нет никаких изменений, обмен двумя α-частицами означает то же самое, что обмен четырьмя парами ферми-частиц. Каждая пара меняет

знак, и в итоге амплитуды складываются со знаком плюс. Так что α-частица ведет себя как бозе-частица. Значит, правило состоит в том, что сложные объекты в тех обстоятельствах, когда их можно считать неделимыми объектами, ведут себя как бозе- или ферми-частицы, смотря по тому,

содержится ли в них четное или нечетное число ферми-частиц.

Состояния с n бозе-частицами.

Рассмотрим тот случай, когда имеются n частиц. Вообразим случай, изображенный на фиг. 2.4.

Есть n частиц а, b, с,..., которые рассеиваются в направлениях 1, 2, 3,..., n. Все n направлений смотрят в небольшой счетчик, который стоит где-то поодаль. Выберем нормировку всех амплитуд так, чтобы вероятность того, что каждая частица, действуя по отдельности, попадет в элемент поверхности dS счетчика, была равна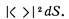

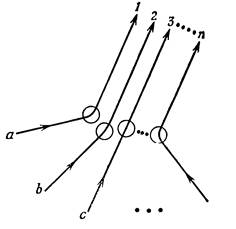
Сперва предположим, что частицы все различимы, тогда вероятность того, что n частиц будут одновременно зарегистрированы в n разных элементах поверхности, будет равна

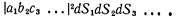
Примем, что амплитуды не зависят от того, где в счетчике расположен элемент dS (он считается малым), и обозначим их просто a, b, с,.... Вероятность (2.15) обратится в

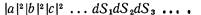
Прогоняя каждый элемент dS по всей поверхности dS счетчика, получаем, что Рп(разные) — вероятность одновременно зарегистрировать n разных частиц — равна

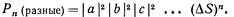
Это просто произведение вероятностей попаданий в счетчик каждой из частиц по отдельности. Все они действуют независимо — вероятность попасть для одной из них не зависит от того, сколько других туда попало. Теперь предположим, что все эти частицы — идентичные бозе-частицы. Для каждой совокупности направлений 1, 2, 3,... существует много неразличимых возможностей. Если бы, скажем, частиц было только три, появились бы следующие возможности:

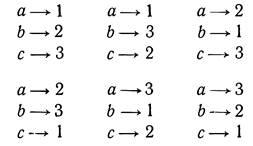
Если частиц n, то будет n! разных, хотя и не отличимых друг от друга, комбинаций; их амплитуды положено складывать. Вероятность того, что n частиц будут зарегистрированы в n элементах поверхности, тогда будет равна

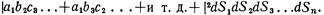
Предположим, что все направления столь близки друг к другу, что можно будет положить а1=а2=...=аn=а

и то же сделать с b, с,...; вероятность обратится в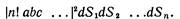

Когда каждый элемент dS прогоняют по площади dS счетчика, то всякое мыслимое произведение элементов поверхности считается n! раз; учтем это, разделив на n!, и получим

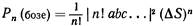
Видим, что вероятность совместного счета n бозе-частиц в n! раз больше, чем получилось бы в

предположении, что· все частицы различимы. Все это можно подытожить так:

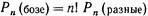
Итак, вероятность в случае бозе-частиц в n! раз больше, чем вы получили бы, считая, что частицы действовали независимо. Мы лучше поймем, что это значит, если спросим: чему равна вероятность того, что бозе-частица перейдет в некоторое состояние, в котором уже находятся n других частиц? Обозначим добавленную частицу буквой w. Если всего, включая w, имеется (n+1) частиц, то

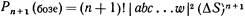
Это можно записать так:

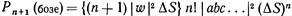
или

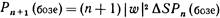
Этот результат можно истолковать следующим образом. Число 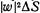— это вероятность заполучить в счетчик частицу до, если никаких других частиц нет; Рn(бозе) — это шанс того, что там уже есть п других бозе-частиц. Значит когда у нас уже есть n других идентичных друг другу бозе-частиц, то вероятность того, что ещё одна частица придет в то же состояние, усиливается в (n+1) раз. Вероятность получить еще один бозон там, где уже есть их п штук, в (n+1) раз больше той, какая была бы, если бы там раньше ничего не было. Наличие других частиц увеличивает вероятность заполучить еще одну.

Принцип запрета

Ферми-частицы ведут себя совершенно по другому нежели бозе-частицы. Посмотрим, что произойдет, если мы попытаемся поместить две ферми-частицы в одно и то же состояние. Вернемся к нашему первоначальному примеру и поинтересуемся амплитудой того, что две идентичные ферми-частицы рассеются в почти одинаковом направлении. Амплитуда того, что частица а пойдет в направлении 1, а частица b — в направлении 2, есть

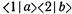
тогда как амплитуда того, что направления вылетающих частиц обменяются местами, такова:

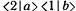
Раз мы имеем дело с ферми-частицами, то амплитуда процесса является разностью этих двух амплитуд:

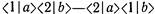
Если теперь позволить направлениям 1 и 2 сблизиться друг с другом, то полная амплитуда в уравнении станет равной нулю. Вы никогда не обнаружите два электрона в одинаковом положении и со спинами, направленными в одну сторону. Двум электронам невозможно иметь

один и тот же импульс и одно и то же направление спина. Если они оказываются в одном и том же месте или в одном и том же состоянии движения, то единственное, что им остается,— это завертеться навстречу друг другу. Стало быть, существует взаимодействие, стремящееся расположить спины навстречу друг другу, когда электроны сближаются. Если два электрона пытаются попасть в одно и то же место, то спины стремятся выстроиться навстречу друг другу.

Эта кажущаяся сила, стремящаяся ориентировать спины в разные стороны, намного мощнее слабеньких сил, действующих между магнитными моментами двух электронов.

Пример влияния принципа запрета.

Мы уже говорили ранее, что ядерные силы, действующие между нейтроном и протоном, между протоном и протоном и между нейтроном и нейтроном, одинаковы. Почему же так получается, что протон с нейтроном могут пристать друг к другу, образовав ядро дейтерия, а вот ядер просто с двумя протонами или просто с двумя нейтронами не существует? Действительно, дейтрон

связан энергией около 2,2 Мэе, а соответствующей связи между парой протонов, которая бы создала изотоп гелия с атомным весом 2, не существует. Таких ядер не бывает. Комбинация двух протонов не дает связанного состояния. Ответ складывается из двух эффектов: во-первых, из

принципа запрета; во-вторых, из того факта, что ядерные силы довольно чувствительны к направлению спина. Силы, действующие между нейтроном и протоном,— это силы притяжения;

они чуть больше, когда спины параллельны, и чуть меньше, когда они направлены противоположно. Оказывается, что различие между этими силами достаточно велико, чтобы дейтрон возникал лишь в том случае, когда спины нейтрона и протона параллельны, а когда спины противоположны, то притяжения не хватает на то, чтобы связать частицы воедино. Поскольку спины нейтрона и протона каждый равен V2 и направлены они в одну сторону, то спин дейтрона равен единице. Мы знаем, однако, что двум протонам не разрешается сидеть друг на друге, если их спины параллельны. Если бы не было принципа запрета, два протона были бы связаны. Но раз они не могут существовать в одном месте и с одним и тем же направлением спина, ядра Не2 не существует. Протоны с противоположными спинами могли бы сойтись, но тогда им не хватило бы энергии связи для образования стабильного ядра, потому что ядерные силы при противоположных спинах чересчур слабы, чтобы связать пару нуклонов. В том, что силы притяжения между нейтронами и протонами с противоположными спинами существуют, можно

убедиться из опытов по рассеянию. Сходные же опыты по рассеянию двух протонов с параллельными спинами показывают, что и между ними существует притяжение. Итак, принцип

запрета помогает нам понять, почему дейтерий может существовать, а Не2 нет.

Обменное взаимодействие

Уравнении Шредингера не учитывается наличие у частиц спина, отнюдь не обесценивает это уравнение и все получающиеся с его помощью результаты.

Дело в том, что электрическое взаимодействие частиц не зависит от их спинов. Математически это означает, что гамильтониан системы электрически взаимодействующих частиц (в отсутствие магнитного поля) не содержит операторов спина и потому при применении его к волновой функции никак не воздействует на спиновые переменные. Поэтому уравнению Шредингера удовлетворяет в действительности каждая из компонент волновой функции; другими словами, волновая функция системы частиц может быть написана в виде произведения

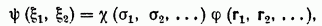
Где первая функция зависит только от координат частиц, а вторая функция — только от их спинов; о первой будем говорить как о координатной или орбитальной, а о второй — как о спиновой волновой функции.

Несмотря на указанную независимость электрического взаимодействия частиц от их спина, существует своеобразная зависимость энергии системы от ее полного спина, проистекающая в конечном итоге из принципа неразличимости одинаковых частиц.

Рассмотрим систему, состоящую всего из двух одинаковых частиц. В результате решения уравнения Шредингера мы найдем ряд уровней энергии, каждому из которых соответствует определенная симметричная или антисимметричная координатная волновая функция.

Перестановка двух одинаковых частиц эквивалентна операции инверсии системы координат (начало которой выбрано посредине прямой, соединяющей обе частицы). С другой стороны, в результате инверсии волновая функция должна умножиться на 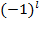, где l — орбитальный момент относительного движения обеих частиц.Мы приходим к выводу, что система из двух одинаковых частиц с целым спином может обладать только четным орбитальным моментом.

Далее, пусть система состоит из двух частиц со спином 1/2 (скажем, электронов). Тогда полная волновая функция системы должна быть непременно антисимметричной по отношению к перестановке обеих частиц. Поэтому при симметричной координатной функции спиновая функция должна быть антисимметричной, и наоборот. Будем писать спиновую функцию в спинорном виде, т. е. в виде спинора второго ранга 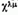каждый из индексов которого соответствует спину одного из электронов. Симметричной по спинам обеих частиц функции соответствует симметричный спинор а антисимметричной — антисимметричный спинор 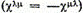Но мы знаем, что симметричный спинор второго ранга описывает систему с равным единице полным спином, а антисимметричный спинор сводится к скаляру, что соответствует равному нулю спину.

Таким образом, мы приходим к следующему результату. Те уровни энергии, которым соответствуют симметричные решения уравнения Шредингера, могут фактически осуществляться при равном нулю полном спине системы, т. е. когда спины обоих электронов «антипараллельны», давая в сумме нуль. Значения же энергии, связанные с антисимметричными функциями требуют равного единице полного спина, т. е. спины обоих электронов должны быть «параллельными».

Другими словами, возможные значения энергии системы электронов оказываются зависящими от ее полного спина. На этом основании можно говорить о некотором своеобразном взаимодействии частиц, приводящем к этой зависимости. Это взаимодействие называют обменным. Оно представляет собой чисто квантовый эффект, полностью исчезающий (как и самый спин) при предельном переходе к классической механике.

Список литературы

1. Л.Д.Ландау и Е.М.Лифшиц “Квантовая механика. Нерелятивистская теория” ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ФИЗИКО-МАТЕАТИЧЕСКОЙ ЛИТЕРАТУРЫ ИОСКВА 1963

2. Фейнман, Лэйтон, Сэндс “Фейнмановские лекции по физике. 8,9 Квантовая механика” ИЗДАТЕЛЬСТВО “МИР” МОСКВА 1978