Завдання 2

Деяке підприємство займається виробництвом продукції чотирьох видів А, Б, В, Д, використовуючи для цього ресурси трьох видів R1, R2, R3. Треба знайти такий план виробництва, при якому вартість усієї виготовленої продукції буде найбільшою. Норми затрат ресурсів на одиницю продукції, запаси сировини та ціна одиниці продукції кожного виду подано в таблиці. Визначити оптимальний план виробництва продукції.

Розв‘язок.

Запишемо обмеження та критерій для даної задачі. Обмеження виражають той факт, що затрати сировини на виробництво не повинні перевищувати її запасів. Критерієм є загальний прибуток від реалізації продукції.

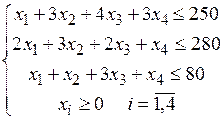
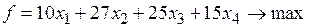
Запишемо дану задачу в канонічній формі, перетворивши нерівності в рівності за допомогою додаткових невідомих x₅, x₆, x₇ (їх додамо до лівих частин нерівностей, щоб зрівняти ліву і праву частини).

Одержимо задачу:

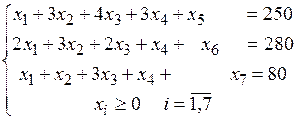
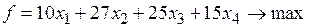
Очевидно, що праві частини додатні, кількість обмежень m=3 і серед векторів A_i є три одиничних (A₅, A₆, A₇) і вони лінійно незалежні, отже утворюють базис. Невідомі x₅, x₆, x₇ є базисними, а всі інші – вільними. Якщо вільним невідомим надати значення 0, то отримаємо x₅=250, x₆=280, x₇=80. Отже вектор (0,0,0,0,250,280,80)є першим опорним розв‘язком Тепер можна починати обчислення за симплекс–методом. Будемо це робити за допомогою таблиць

Таблиця 1

Таблицю 1 заповнюємо так: в стовпчику “A0” в перших m рядках, тобто в перших трьох рядках записуємо числа, що стоять в правих частинах системи. В стовпчиках “Ai” (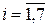) в тих самих рядках записуємо коефіцієнти при невідомих x_i(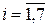) цієї системи відповідно. В стовпчику ”Базис” записуємо вектори, що утворюють базис для першого опорного розв‘язку (тобто А5, А6 і А7), а в стовпчику “оцінка“ напроти базисних векторів записуємо коефіцієнти при відповідних невідомих в цільовій функції (тобто при х5, х6 і х7, а це с5=0, с6=0 і с7=0). В стовпчиках Аі, над Аi записуємо коефіцієнти при невідомих хі (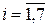) в цільовій функції. Далі заповнюємо m+1-й, тобто четвертий рядок. В стовпчиках “Базис” і “оцінка” нічого не пишемо. В стовпчику “A0” записуємо число Z1, яке дорівнює сумі добутків чисел із стовпчика “оцінка“ на відповідні числа із стовпчика “А0”:

Z1– це значення цільової функції для першого опорного плану, відмінні від нуля координати якого стоять в стовпчику “А0”. В стовпчиках j « Ai » в (m + 1) рядку записуємо числа Δ_i, які дорівнюють різниці між сумою добутків чисел із стовпчика «оцінка» на відповідні числа із стовпчика «Ai» та коефіцієнта при невідомому x_iв цільовій функції. Ці числа називаються оцінками.

З теорії симплекс–методу відомо, що оптимальним буде той план, для якого всі оцінки Δ_i невід’ємні.

В нашій таблиці серед оцінок Δ_i є від‘ємні. Отже, план не є оптимальним. Далі треба подивитися, чи є серед чисел, що стоять в стовпчиках з від‘ємними оцінками, додатні числа. Якщо хоча б в одному з таких стовпчиків додатних чисел немає, то задача розв‘язку не має. Якщо додатні числа є в кожному із стовпчиків, де стоять від‘ємні оцінки, то можна знайти кращий план. З таблиці видно, що в тих стовпчиках, де стоять від‘ємні оцінки є додатні числа. Тому можна знайти кращий план. Для цього треба один із базисних векторів вивести з базису, а замість нього ввести в базис один із небазисних векторів. Для цього серед від‘ємних оцінок вибираємо найбільшу за модулем (якщо таких декілька, то вибираємо одну із них, все одно яку). В нашому прикладі це Δ₁ = -27. Далі, для кожного додатного числа, яке стоїть в стовпчику “Ai” над найбільшою за модулем від‘ємною оцінкою Δ_i (тобто над Δ₁ = -27 − в другому стовпчику) знаходять відношення числа із стовпчика “A0” до цього числа. Для нашої таблиці це відношення дорівнює 80. Число a_ij, для якого це відношення є найменшим, називають розв‘язувальним елементом. Для нашого прикладу це число 1. Рядок і стовпчик, на перетині яких стоїть розв‘язувальний елемент, називаються розв‘язувальними. В нашому прикладі це третій рядок і другий стовпчик.

З базису виводиться той вектор, що стоїть в розв‘язувальному рядку, а водиться в базис той вектор, що стоїть в розв‘язувальному стовпчику. В нашій таблиці з базису виводиться вектор A7, а вводиться вектор A2. Далі переходимо до нового опорного плану, заповнюючи для цього таблицю 2. В таблиці 2, в стовпчику “Базис”, записуємо новий базис (замість A7 вписуємо A2), в стовпчику “оцінка“ записуємо коефіцієнти с1=0, с6=0, с7=27 при невідомих x₅x₄ x₇ в цільовій функції. Далі заповнюємо стовпчики, які відповідають базисним векторам. Ці вектори повинні бути одиничними. В стовпчику “А2“ в рядочку, де стоїть А2, ставимо 1, а в інших рядках ставимо нулі. Стовпчики ”А5” та ”А6” залишаються такими самими, як і в першій таблиці, тому що вектор А5 та А6 залишилися в базисі. Далі елементи розв‘язувального (другого) рядка ділимо на розв‘язувальний елемент, тобто на 1, і записуємо отримані числа на відповідні місця в другій таблиці.

Всі інші числа, включаючи і числа з m+1 (тобто з третього рядка), отримаємо за методом Джордано–Гауса (правило прямокутників).

Таблиця 2

Оскільки в останньому рядку другої таблиці немає від‘ємних чисел (оцінок), то план, що відповідає цій таблиці, є оптимальним. Його додатні координати записані в стовпчику “А0” другої таблиці: В цьому ж стовпчику в останньому рядку записане значення цільової функції для цього плану

Отже, отриманий розв‘язок задачі x₁ = 0, x₂ = 80, x₃ = 0, x₄ = 0, x₅ =10, x₆=40, x₇ = 0, одержаний прибуток F_max = 2160