Тема: Нахождение высоты, боковых ребер призмы

Рабочий лист.

Предмет	Математика
Группа	№ 5 2 курс
Тема урока	Нахождение высоты, боковых ребер призмы.
ФИО преподавателя	Тимиршина Алия Мунзиловна
Где находится задание:
Учебник	Погорелов А.В.«Геометрия 10 - 11» (М.:Просвещение, 2010 и последующие издания)
Ссылка	http://padabum.com/d.php?id=21202
Сроки выполнения задания	30.09.2020 до 17:00
Как выполнять задание	Используя методические указания решить задачи, выполнить домашнее задание.
Домашняя работа	Погорелов А.В.«Геометрия 10 - 11», §5 №35
Обратная связь	Выполненные работы отправить личным сообщением ВК
Как узнать отметку о выполненном задании	Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК.

Практическая работа.

Тема: Нахождение высоты, боковых ребер призмы.

Методические указания

Призма – это объемное тело, которое имеет большое количество граней.

Данная фигура имеет в основаниях два многоугольника, которые расположены в параллельных плоскостях, а все боковые грани имеют форму параллелограмма.

Рис 1. Рис. 2

Итак, давайте разберемся, из чего состоит призма. Для этого обратите внимание на Рис.1

Как уже говорилось ранее, у призмы есть два основания, которые параллельны друг другу – это пятиугольники ABCEF и GMNJK. Более того, данные многоугольники равны между собой.

Все остальные грани призмы называются боковыми гранями – они состоят из параллелограммов. Например, BMNC, AGKF, FKJE и т.д.

Общая поверхность всех боковых граней называется боковой поверхностью.

Каждая пара соседних граней имеет общую сторону. Такая общая сторона называется ребром. Например МВ, СЕ, АВ и т.д.

Если верхнее и нижнее основание призмы соединить перпендикуляром, то он будет называться высотой призмы. На рисунке высота отмечена, как прямая ОО₁.

Существует две основных разновидности призмы: наклонная и прямая.

Если боковые ребра призмы не являются перпендикулярными к основаниям, то такая призма называется наклонной.

Если все ребра призмы перпендикулярны к основаниям, то такая призма называется прямой.

Если в основаниях призмы лежат правильные многоугольники (те, у которых стороны равны), то такая призма называется правильной.

Если основания у призмы не параллельны друг другу, то такая призма будет называться усеченной.

Её Вы можете наблюдать на Рис.2

Формулы для нахождения объема, площади призмы

Существует три основных формулы нахождения объема. Отличаются они друг от друга применением:

Аналогичные формулы для нахождения площади поверхности призмы:

Основные свойства призмы:

Верхнее и нижнее основание равны между собой.
Каждая призма имеет параллелограмм в виде боковой грани.
Все ребра параллельны друг другу.
Если Вам дана прямая призма, то можете быть уверенны, что её боковое ребро равно высоте.
Если же Вы имеете наклонную призму, то её ребро всегда длиннее, чем высота такой призмы.
У прямой призмы гранями являются либо прямоугольники, либо квадраты

Задания:

Задача 1

Основанием прямой призмы является равнобедренная трапеция с основаниями 21см и 9 см и высотой 8 см (рис. 3). Найдите площадь боковой поверхности, если боковое ребро равно 10 см.

Рис. 3

Дано: AD ∥ BC, AB = CD,

AD = 21см, BC = 9см, BH = 8 см,

АА₁ ⊥ АВС, АА₁ = 10 см. (рис. 4)

Найти: S_бок

Рис. 4

Решение:

Рассмотрим трапецию ABCD (рис. 5). ВН и CG – высоты трапеции. AD = 21см, BC = 9см. Так как трапеция ABСD равнобокая, то HG = BC = 9 см, (см).

Рис. 5

Рассмотрим треугольник ∆ АВН и найдем сторону АВ по теореме Пифагора:

Найдем периметр основания.

Применяем формулу для площади боковой поверхности:

Ответ: 500 см²

Задача 2

Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство проведём на примере треугольной призмы.

Рис. 6

Рассмотрим треугольную призму АВСА₁В₁С₁. Построим плоскость перпендикулярного сечения. На ребре ВВ₁ выберем точку К (рис. 7). Через точку К можно проведем перпендикуляр KL в плоскости этой грани АА₁В₁В к ребру ВВ₁. Этот перпендикуляр будет перпендикуляром и к АА₁, так как прямые АА₁ и ВВ₁ параллельны..

Теперь проведем перпендикуляр КМ перпендикулярно ребру ВВ₁ в плоскости грани ВВ₁С₁С.

Получаем, что боковое ребро ВВ₁ перпендикулярно двум пересекающимся прямым KL и КМ плоскости KLM. Значит, ВВ₁ - перпендикуляр к плоскости KLM.

То есть, построенное сечение KLM перпендикулярно боковому ребру. Надо доказать, что площадь боковой поверхности равняется произведению периметра перпендикулярного сечения KLM на боковое ребро ВВ₁. То есть, имеем следующую задачу.

Рис. 7

Дано: АВСА₁В₁С₁ – наклонная призма,

ВВ₁ ⊥ KLM.

Доказать:

Доказательство:

Любая боковая грань призмы – это параллелограмм. Рассмотрим грань АВВ₁А₁. KL – это высота параллелограмма АВВ₁А₁. Поэтому площадь параллелограмма АВВ₁А₁ записывается следующим образом:

Аналогично, , .

В призме все боковые ребра равны, АА₁ = ВВ₁ = СС₁. Запишем, чему равна площадь боковой поверхности.

Мы показали, что . Задача доказана.

Задача 3

Основание призмы – правильный треугольник АВС (рис. 8). Боковое ребро АА₁ образует равные острые углы со сторонами основания АВ и АС. Докажите, что

a) BC ⊥ AA₁;

b) грань ВВ₁С₁С – прямоугольник.

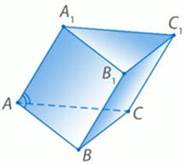
Рис. 8

Дано: АВСА₁В₁С₁ – призма.

АВ = ВС = АС,

∠А₁АВ = ∠А₁АС,

∠А₁АВ < 90°.

Доказать:

a) BC ⊥ AA₁;

b) грань ВВ₁С₁С – прямоугольник.

Рис. 9

Доказательство:

а) Проведём перпендикуляр А₁О к плоскости АВС. Из точки О опустим перпендикуляры ОМ к АВ и OL к АС.

А₁О - перпендикуляр к плоскости АВС. ОМ – проекция наклонной А₁М на плоскость АВС. Так как проекция ОМ перпендикулярна прямой АВ из плоскости АВС, то и наклонная А₁М перпендикулярна прямой АВ (по теореме о трех перпендикулярах).

ОL – проекция наклонной А₁L на плоскость АВС. Так как проекция ОL перпендикулярна прямой АC из плоскости АВС, то и наклонная А₁L перпендикулярна прямой АC (по теореме о трех перпендикулярах).

Получаем, что треугольники А₁АМ и А₁АL – прямоугольные. В этих треугольниках гипотенуза АА₁ – общая и углы ∠А₁АВ и ∠А₁АС равны. Значит, треугольники А₁АМ и А₁АL равны по гипотенузе и острому углу.

Из равенства треугольников имеем: АМ = АL и А₁М = А₁L.

Рассмотрим прямоугольные треугольники АОМ и АОL. Гипотенуза АО общая, катеты АМ и АL равны. Из равенства треугольников получаем равенство углов: ∠ ОАМ = ∠ ОАL.

Так как ∠ ОАМ = ∠ ОАL, то АО – биссектриса. Треугольник АВС – равносторонний, значит, АО - и биссектриса, и медиана, и высота. То есть прямая ВС из плоскости треугольника АВС перпендикулярна АО, а АО – это проекция наклонной АА₁. Значит, прямая ВС и АА₁ перпендикулярны по теореме о трех перпендикулярах.

б) Все боковые ребра между собой параллельны. Мы доказали, что прямая ВС перпендикулярна одному боковому ребру, значит прямая ВС перпендикулярна и остальным боковым ребрам, ВС ⊥ ВВ₁, ВС ⊥ СС₁. А это означает, что параллелограмм ВВ₁С₁С является прямоугольником, что и требовалось доказать.

Задача 4

Сторона основания правильной четырехугольной призмы равна а, диагональ призмы образует с плоскостью основания угол 45°. Найдите:

а) диагональ призмы;

б) угол между диагональю призмы и плоскостью боковой грани;

в) площадь боковой поверхности призмы.

Рис. 10

Дано: ABCD – квадрат,

АВ = а, АА₁ ⊥ АВС.

∠(АС₁, АВС) = 45°.

Найти:

а) АС₁;

б) ∠(АС₁, АD₁C₁);

в) S_бок

Решение:

а) ABCDA₁B₁C₁D₁ - правильная четырехугольная призма. Это означает, что в её основании лежит квадрат АВСD.

Сторона квадрата АВСD по условию равна а, тогда диагональ АС = а√2.

Угол между диагональю АС₁ и плоскостью основания ABC равен 45°. Угол между диагональю АС₁ и плоскостью основания ABC – это угол между прямой АС₁ и её проекцией на плоскость ABC, то есть угол С₁АС, значит, ∠ С₁АС = 45°. Так как треугольник С₁АС прямоугольный, то и угол АС₁С равен 45°. Значит, треугольник С₁АС – равнобедренный. Значит, СС₁ = АС = а√2.

Из прямоугольного треугольника АС₁С находим по теореме Пифагора АС₁.

Ответ: 2а.

б) Прямая С₁D₁ перпендикулярна всей плоскости АDD₁. Угол между прямой АС₁ и гранью АDD₁ - это угол между прямой АС₁ и её проекцией АD₁ на плоскость АDD₁. Значит, искомый угол - ∠ С₁АD₁.