Задачи на экстремум имеют большое значение в экономических расчетах. Это вычисление, например, максимумов дохода, прибыли, минимума издержек в зависимости от нескольких переменных: ресурсов, производственных фондов и т.д.
Теория нахождения экстремумов функций нескольких переменных излагается в базовом курсе математики. Напомним основные моменты.
Частная производная функции 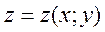 по аргументу, например, х является обыкновенной производной функции одной переменной х при фиксированном значении у.
по аргументу, например, х является обыкновенной производной функции одной переменной х при фиксированном значении у.
Точка 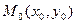 , в которой для дифференцируемой функции
, в которой для дифференцируемой функции  выполняется условие (необходимое условие существования локального экстремума):
выполняется условие (необходимое условие существования локального экстремума):
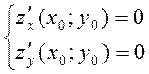 , (8.1)
, (8.1)
называется критической точкой возможного экстремума или стационарной точкой.
Теорема (достаточное условие локального экстремума). Пусть в точке 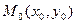 и в некоторой ее окрестности все вторые частные производные функции
и в некоторой ее окрестности все вторые частные производные функции  непрерывны. Тогда, если
непрерывны. Тогда, если
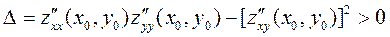 , (8.2)
, (8.2)
то функция 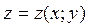 имеет в точке М0 локальный экстремум: максимум при
имеет в точке М0 локальный экстремум: максимум при 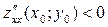 и минимум при
и минимум при 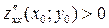 . Если
. Если 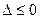 , то данная функция не имеет локального экстремума в точке М0..
, то данная функция не имеет локального экстремума в точке М0..
Пример 1. Небольшая фирма производит два вида товаров G1 и G2 и продает их по цене 1000 и 800 соответственно. Функция затрат (издержек) имеет вид:
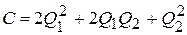 , (8.3)
, (8.3)
где Q1 и Q2 обозначают объёмы выпуска соответственно товаров G1 и G2.
Требуется найти такие значения Q1 и Q2, при которых прибыль, получаемая фирмой, максимальна.
Поскольку фирма небольшая, она не может монопольно устанавливать цены и вынуждена ориентироваться на рыночные цены, которые не зависят от объёмов производства Q1 и Q2 (эти объёмы слишком малы). Поэтому суммарный доход от продажи товаров G1 и G2
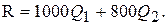 (8.4)
(8.4)
Прибыль p представляет собой разницу между доходом R и затратами C, поэтому
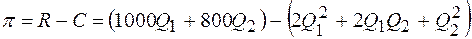 , (8.5)
, (8.5)
или
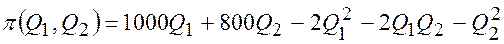 . (8,6)
. (8,6)
Эта и есть та самая функция двух переменных, максимум которой следует найти, т.е. решить задачу оптимизации.
Для того, чтобы найти стационарные точки, вычисляем частные производные первого порядка
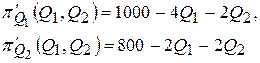
и приравниваем их к нулю, что дает систему двух уравнений с двумя неизвестными
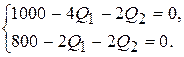
Решение этой системы и даст нам координаты стационарной точки. Вычитая из первого уравнения почленно второе, получаем
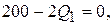
или
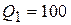 . (8.7)
. (8.7)
Подставляя полученное значение в первое уравнение, находим
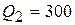 . (8,8)
. (8,8)
Таким образом, стационарная точка имеет координаты
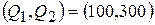 .
.
Остается выяснить вопрос: имеем ли мы в стационарной точке максимум, минимум или не имеем ни того, ни другого. Для решения вычисляем частные производные второго порядка
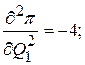
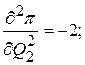
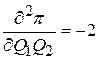
и оставляем выражение
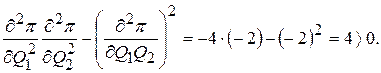 (8.9)
(8.9)
Кроме того,
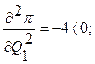
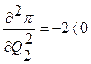 . (8.10)
. (8.10)
Поэтому в стационарной точке имеет место максимум. Подставляя координаты стационарной точки в функцию прибыли
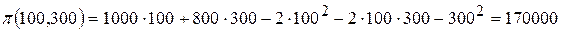 .
.
Это и есть величина максимальной прибыли, которая достигается при объёмах производства Q1=100; Q2=300, что завершает решение задачи.
Учитывая актуальность получения максимальной прибыли при любой предпринимательской деятельности, разберем следующую задачу.
Пример 2. Фирма реализует часть товара на внутреннем рынке, а другую часть поставляет на экспорт. Связь цены товара q1 и его количества р1, проданного на внутреннем рынке, описывается кривой спроса с уравнением:
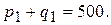
Аналогично для экспорта количество р2 и цена q2, также связаны соотношением (уравнением кривой спроса)
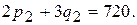
Суммарные затраты даются выражением
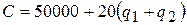 .
.
Спрашивается какую ценовую политику должна проводить фирма, чтобы прибыль была максимальна.
Прежде всего необходимо определить доход фирмы, который складывается из двух частей: продаж на внутреннем рынке
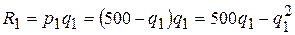
и экспортных поставок

(в обоих случаях цена берется из соответствующих кривых спроса).
Поэтому суммарный доход
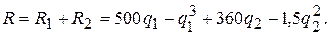
Теперь можно легко найти получаемую фирмой прибыль
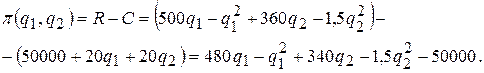
Эта функция двух переменных, нахождение максимума которой и решает задачу оптимизации.
Вычисляем частные производные первого порядка
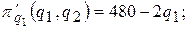
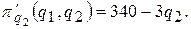
Приравнивая их к нулю, получаем систему двух уравнений с двумя неизвестными
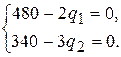
В данном случае система решается тривиально
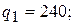
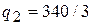 ,
,
и мы получили координаты единственной стационарной точки.
Далее вычисляем частные производные второго порядка
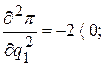
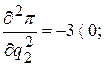
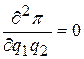
и проверяем знак выражения
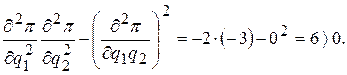
Отсюда заключаем, что в стационарной точке (240,340/3) имеет место максимум.
Для того чтобы ответить на вопрос об оптимальной ценовой политике фирмы, подставляем координаты точки максимума в кривые спроса:
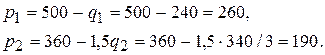
Это и есть оптимальные цены для продажи на внутреннем рынке и по экспорту.
Нам осталось подсчитать максимальную прибыль при оптимальных объёмах продаж на внутреннем и внешнем рынках. Подставляя полученные значения q1 и q2 (координаты стационарной точки) в функцию прибыли, легко находим эту прибыль
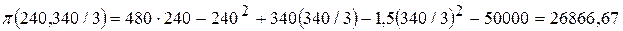 .
.
Рассмотрим частный случай более общей задачи нелинейного программирования, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных и 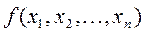 и
и 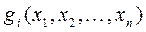 - функции, непрерывные вместе со своими частными производными
- функции, непрерывные вместе со своими частными производными
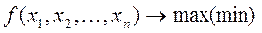 ; (8.11)
; (8.11) 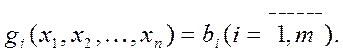 (8.12)
(8.12)
Задачу (5.11) - (5.12) называют задачей на условный экстремум или классической задачей оптимизации.
Чтобы найти решение этой задачи, вводят набор переменных 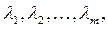 называемых множителями Лагранжа,составляют функцию Лагранжа
называемых множителями Лагранжа,составляют функцию Лагранжа
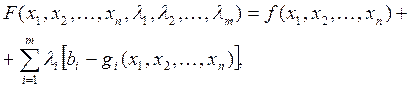 (8.13)
(8.13)
находят частные производные 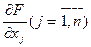 и
и 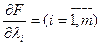 и рассматривают систему
и рассматривают систему 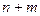 уравнений
уравнений
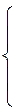
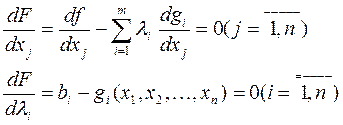 (8.14)
(8.14)
с 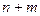 неизвестными
неизвестными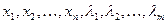 . Всякое решение системы уравнений (5.14) определяет точку
. Всякое решение системы уравнений (5.14) определяет точку 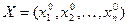 , в которой может иметь место экстремум функции
, в которой может иметь место экстремум функции 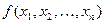 . Следовательно, решив систему уравнений (5.14), получают все точки, в которых функция (5.11) может иметь экстремальные значения. Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума.
. Следовательно, решив систему уравнений (5.14), получают все точки, в которых функция (5.11) может иметь экстремальные значения. Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума.
Таким образом, определение экстремальных точек задачи (8.11) -(8.12) методом множителей Лагранжа включает следующие этапы:
1. Составляют функцию Лагранжа.
2. Находят частные производные от функции Лагранжа по переменным 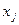 и
и 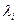 и приравнивают их нулю.
и приравнивают их нулю.
3. Решая систему уравнений (8.14) находят точки, в которых целевая функция задачи может иметь экстремум.
4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значения функции (8.11) в этих точках.
Дальше приводится задача на нахождение условного экстремума методом Лагранжа (пример 3)
Пример 3. Фирма-монополист производит два вида товаров G1 и G2 в количестве q1 и q2 соответственно. Функция затрат имеет вид:
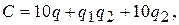
а кривые для спроса для каждого товара:
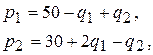
где р1 и р2 – цена единицы соответственно товаров G1 и G2. Кроме того, фирма связана ограничением на общий объём производства товаров G1 и G2, её квота составляет 15 единиц, т.е.
q1+q2=15.
Требуется найти максимальную прибыль, которая может быть достигнута при этом условии.
Решение задачи начнем с построения целевой функции, в данном случае прибыли, которая определяется как разница между доходами и затратами:
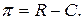
Для дохода от продажи товара G1 имеем:
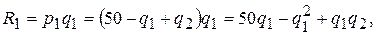
где выражение для р1 берется из кривой спроса товара G1. Аналогично доход от продажи товара G2:
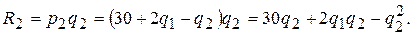
Очевидно, что суммарный доход будет
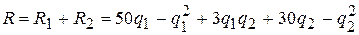 .
.
Поскольку затраты известны из условия задачи, то прибыль (целевая функция) имеет вид:
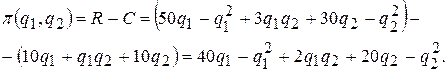
Переписав ограничение в виде
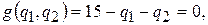
получаем задачу условной оптимизации (поиска условного экстремума). Для её решения применим метод Лагранжа.
Строим вспомогательную функцию
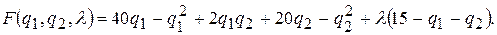
Вычисляем частные производные и приравниваем их к нулю:
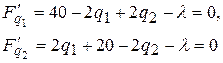
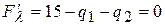
Мы получили систему трех уравнений с тремя неизвестными. Представляем её в виде
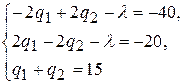
и решаем методом исключения. Для этого складываем первое и втрое уравнения, что дает
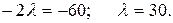
Подставляя в первое уравнение, полученное значение, получаем
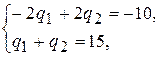
т.е. систему двух уравнений с двумя неизвестными. Решая её, легко находим
q1=10; q2=5.
Это и есть координаты точки условного экстремума, т.е. тот объём продаж, при котором прибыль максимальна. Соответствующее значение самой прибыли будет
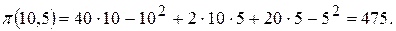
 2014-02-04
2014-02-04 4197
4197