Символьная соционика: личный опыт понимания и применения

ЗАДАЧИ

Нумерация узлов.

Нумерация влияет на эффективность вычислений. Использование МКЭ приводит к решению системы линейных алгебраических уравнений, в которых большинство коэффициентов нулевые. Расстояние между главной диагональю матрицы коэффициентов и линией, за которой только нулевые коэффициенты называется шириной полосы матрицы. Ширина полосы матрицы B вычисляется по формуле

B=(R+1)Q, (1)

где R – максимальная величина разности между номерами узлов по всем КЭ, Q – число степеней свободы в каждом узле.

Чем меньше R, тем меньше B. Нужно двигаться при нумерации в направлении наименьшего размера области. Пример.

1. Разбейте треугольную область на 16 КЭ, пронумеруйте узлы и вычислите ширину полосы при наличии 2 степеней свободы. Рассмотреть 2 варианта нумерации, число узлов на каждой стороне – 5, B₁=14, B₂=24.

2. Разбейте четырехугольник на 24 элемента, используя 5 узлов вдоль одной пары сторон и 4 узла вдоль другой пары. Пронумеруйте узлы так, чтобы получить минимальное значение величины R. (R=7 и 10).

3. Разбейте прямоугольный треугольник на 60 элементов, предварительно выделив две треугольные и одну четырехугольную подобласти. Поместите наименьшие по размерам элементы вблизи прямого угла.

4. Разбейте консоль на линейные треугольные КЭ. На закрепленной границе разместите вдвое больше узлов, чем на свободном конце. Укажите с помощью принятых обозначений неподвижно закрепленные концы. Использовать метод 2→3.

Лекция 3. ЛИНЕЙНЫЕ ИНТЕРПОЛЯЦИОННЫЕ ПОЛИНОМЫ

МКЭ основан на идее замены непрерывной функции дискретной моделью, которая строится на основе набора кусочно-непрерывных функций, определенных внутри подобластей, называемых элементами. В качестве функций используются обычно полиномы, порядок которых зависит от числа в пределах элемента.

Классификация КЭ проводится в соответствии с порядком полиномиальных функций. Рассматриваются 3 группы КЭ: симплекс, комплекс и мультиплекс – элементы. Симплекс-элементам соответствуют полиномы, содержащие константу и линейные члены. Число коэффициентов будет на 1 больше размерности пространства. Например: j=a₁+a₂x+a₃y – симплекс-функция для 2-х мерного треугольника. Треугольник имеет 3 узла для определения 3 коэффициентов.

Комплекс-элементам соответствуют функции, содержащие константу, линейные члены и члены 2-го и более высоких порядков. Форма комплекс-элементов может быть такой же, как и у симплексов. Однако комплекс-элементы имеют дополнительные граничные и возможно внутренние узлы. Число узлов в комплекс-элементе больше размерности пространства плюс единица. Например, интерполяционный полином для двумерного треугольного комплекс-элемента: j=a₁+a₂x+a₃y+a₄x² +a₅xy+a₆y² – нужно 6 узлов.

Мильтиплекс-элемент также использует полиномы высокого порядка, но его границы должны быть параллельны координатным осям (прямоугольник в прямоугольной системе координат).

Одномерный симплекс-элемент (ОСЭ)

ОСЭ представляет собой прямолинейный отрезок длины L c двумя узлами с индексами i и j, с узловыми значениями функции Ф_i и Ф_j. Начало системы координат располагается вне элемента. Полиномиальная функция имеет вид: j=a₁+a₂x.. (2)

Коэффициенты a₁ и a₂ определяются при решении двух уравнений

Ф_i=a₁+a₂X_i,

Ф_j=a₁+a₂X_j. (3)

Откуда находим значения коэффициентов:

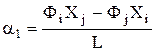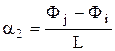; .(4)

Для функции j из уравнения (2) получаем:

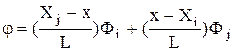. (5)

Линейные функции от x называют функциями-формы (ФФ), или интерполяционными функциями, и обозначают через N. В соотношение (5) входят две ФФ

N_i=(X_j-x)/L и N_j=(x-X_i)/L. (6)

Соотношение (5) можно переписать в матричном виде

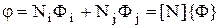. (7)

Функция-форма N_i равна 0 в узле j и равна 1 в узле i. Главным свойств ФФ является равенство 1 в одном узле элемента и 0 во всех остальных узлах.

Двумерный симплекс-элемент

Это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. Используется нумерация узлов против часовой стрелки начиная от некоторого начального узла i, который выбирается произвольно.

Узловые значения скалярной величины j обозначаются через Ф_i, Ф_j Ф_k, а координатные пары узлов – через (X_i,Y_j), (X_j,Y_j) и (X_k,Y_k).

Интерполяционный полином имеет вид

j=a₁+a₂x+a₃y. (8)

В узлах выполняются следующие условия

j=Ф_i при x=X_i, y=Y_i,

j=Ф_j при x=X_j, y=Y_j,

j=Ф_k при x=X_k, y=Y_k, (10)

Подставляя (10) в (9), получаем систему 3 уравнений с 3 неизвестными

Ф_i=a₁+a₂X_i+a₃Y_i

Ф_j=a₁+a₂X_j+a₃Y_j

Ф_k=a₁+a₂X_k+a₃Y_k, (11)

решая которую, получаем

a₁ = [(X_jY_k-X_kY_j)Ф_i+(X_kY_i-X_iY_k)Ф_j+(X_iY_j-X_jY_i)Ф_k]/2A

a₂ = [(Y_j-Y_k)Ф_i+(Y_k-Y_i)Ф_j+(Y_j-Y_i)Ф_k]/2A

a₃ = [(X_k-X_j)Ф_i+(X_i-X_k)Ф_j+(X_j-X_j)Ф_k]/2A, (12)

где 2А – определить системы (11) и А – площадь треугольного элемента.

Подставляя (12) в (8), можно переписать (8) через ФФ в виде

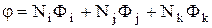,.(13)

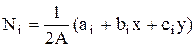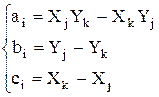
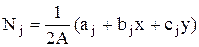где и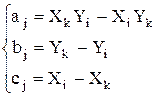

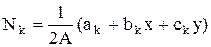и

и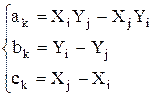

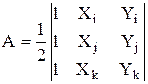- площадь треугольного элемента.

Можно показать, что ФФ N_i равна 1 в узле i и 0 в любом другом узле.

В пределах элемента частные производные от функции j по x и по y – постоянны.

¶j/¶x=¶N_i/¶xФ_i+¶N_j/¶xФ_j+¶N_k/¶xФ_k, (14)

и ¶N_i/¶x=b_i;¶N_j/¶x=b_j;¶N_k/¶x=b_k.

Аналогично

¶j/¶y=¶N_i/¶yФ_i+¶N_j/¶yФ_j+¶N_k/¶yФ_k, (15)

и ¶N_i/¶y=c_i;¶N_j/¶y=c_j;¶N_k/¶y=c_k.

Необходимо использовать очень малые элементы, чтобы аппроксимировать быстро меняющуюся функцию j. Функция j меняется линейно между любыми двумя узлами.

Трехмерный симплекс-элемент

Представляет собой тетраэдр с 4 узлами i, j, k, l. Узел l расположен в вершине тетраэдра, которая находится вне плоскости узлов i, j, k.

Интерполяционный полином его имеет вид

j=a₁+a₂x+a₃y+a₄z. (16)

Коэффициенты находятся из решения системы 4 линейных уравнений по известным узловым значениям функции Ф_i, Ф_j Ф_k, Ф_l

Ф_i=a₁+a₂X_i+a₃Y_i+a₄Z_i

Ф_j=a₁+a₂X_j+a₃Y_j +a₄Z_j

Ф_k=a₁+a₂X_k+a₃Y_k+a₄Z_k. (17)

Ф_l=a₁+a₂X_l+a₃Y_l+a₄Z_l

Система (17) может быть записана в матричной форме

{Ф}=[C]{a}, (18)

где det[C] – определитель матрицы [C] равен 6 объемам тетраэдра.

Задачи.

1. Одномерный симплекс-элемент используется для аппроксимации распределения температуры в стержне. Установлено, что температура в узлах i и j равна 120⁰ и 90⁰. Определить температуру в точке на расстоянии 4 см от начала координат и градиент температуры внутри элемента. Узлы i и j расположены на расстоянии 2см и 6см от начала координат.

2. Требуется получить соотношение, определяющее элемент и вычислить значение давления в точке B c координатами (2,2), если заданы узловые значения P_i=40 н/см², P_j=34 н/см², P_k=46 н/см². Координаты узлов: (X_i,Y_j)- (0,0), (X_j,Y_j)- (4,1) и (X_k,Y_k)-(2,5).

Лекция 4. ИНТЕРПОЛИРОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН. МЕСТНЫЕ СИСТЕМЫ КООРДИНАТ

Необходимо в узлах определять более одной неизвестной. Векторная величина представляется ее компонентами, которые рассматриваются как неизвестные скалярные величины. Каждый узел будет содержать одну, две или три неизвестные в зависимости от размерности задачи.

Для 2-мерного СЭ имеем для перемещений по оси ОХ (u- горизонтальная компонента) и OY(v- вертикальная компонента):

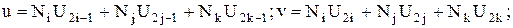(19)

Цифра 2 при узловом значении U в (19) указывает на размерность модели (двумерная).

Либо, с учетом всех узловых значений

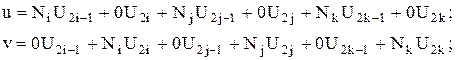(20)

Или в матричном виде

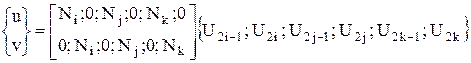(21)

Записать для 3-х мерного СЭ – U_3i-2(u); U_3i-1(v); U_3i(w).

Местная система координат

Получение системы уравнений для узловых неизвестных значений включает интегрированием по площади элемента ФФ и их производных. Сделать это на много проще при использовании местной, или локальной системы координат.

Рассмотрим треугольный элемент и для него скалярную величину 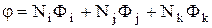. Поместим локальную систему координат (s,t) в его центре, с координатами 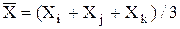; 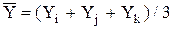. Тогда x=s+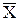; y=t+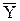.Подставим значения x,y в выражение для N_i в глобальной системе координат:

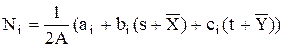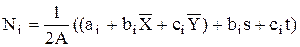или (22)

Поскольку 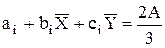, вид N_i в локальной системе координат упростится.

Интеграл по площади элемента при изменении системы координат имеет вид

(23)

где 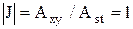- определитель преобразования координат.

Одномерный элемент

Если поместить начало координат в i-том узле, то x=X_i+s и N_i=1-s/L; N_j=s/L. Тогда

j=(1-s/L)Ф_i+s/LФ_j. (24)

L-координаты

Для треугольного элемента обычно используется естественная система координат: L₁; L₂; L₃. Каждая координата является отношением расстояния произвольной точки треугольника до одной из его сторон s к высоте h, опущенной на эту сторону из противоположной вершины. Очевидно, что значения L_i меняются от 0 до 1. Значения L-координат дают относительные величины 3 площадей треугольников A₁, A2, A3 к общей площади треугольника A, на которые делит треугольник любая точка внутри него: L₁=A₁/A; L₂=A₂/A; L₃=A₃/A. Очевидно, что L₁+ L₂+ L₃=1.

L-координаты являются ФФ для треугольного симплекс-элемента, т.е. N_i=L₁; N_j=L₂; N_k=L₃. Очевидно, что L_i =1 в узле I и L_i =0 в узлах j и k.

Можно выразить координаты (x,y) через L-координаты с помощью решения системы уравнений

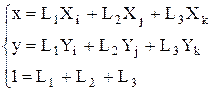(25)

В (25) x и y представляют собой компоненты расстояния и выражаются через свои узловые значения, как любая векторная величина.

Главное преимущество L-координат – это существование интегральных формул, которые упрощают интегрирование по площади элемента и вдоль его сторон.

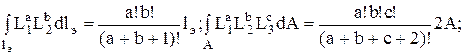(26)

Например, 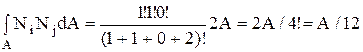, где N_i N_j – функции глобальных координат (x,y).

Для трехмерных СЭ L-координаты называются объемными и связаны соотношением: L₁+L₂+L₃+L₄=1. Для линейного тетраэдра: N_i=L₁; N_j=L₂; N_k=L₃;N_l=L₄. Для вычисления интеграла по объему имеем:

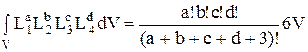. (27)

Свойства интерполяционного полинома

Сходимость

Решение по МКЭ будет сходиться к точному значению с уменьшением размеров элемента, если при равенстве узловых значений на элементе значение самой функции внутри элемента будет постоянным. Это условие накладывает ограничения на ФФ. Предположим, что r узловых значений на элементе равны между собой j=C, тогда

j=N_iФ_i+N_jФ_j+…+N_rФ_r=(N_i+N_j+…+Nr)C. (28)

Тогда из (28) следует, что 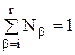, где r – число узлов на элементе.

Например, для одномерного элемента N_i+ N_j= (X_j-x)/L+(x-X_i)/L=1.

Следовательно, сумма значений ФФ в любой точке элемента должна быть равна 1, иначе аппроксимация такими ФФ будет давать ложные результаты.

Критерий равенства нулю частной производной по любому направлению внутри элемента удовлетворяется автоматически при выполнении первого условия (показать это).

Непрерывность.

Чтобы интеграл от n-ой производной был определен, необходимо, чтобы подынтегральная функция была непрерывна вместе со своими (n-1)производными. Следовательно, 1-е частные производные от аппроксимирующей функции должны быть непрерывны на границах элемента, если ДУ содержит производные 2-го порядка.

Задачи

1. Вычислить ФФ для:

1) одномерного элемента i(2) – j(4)

2) двумерного треугольника i(1,1);j(3,0);k(2,3).

2. Заданы узловые перемещения для 2-мерного симплекс элемента: (u_i;v_i)=(2,4), (u_j;v_j)=(6,5); (u_k;v_k)=(-1,-2). Координаты узлов: i(0,0); j (20, -5); k(8,20). Определить перемещения (u_B,v_B) в точке B(10,10).

3. Вычислить интеграл 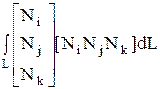, где L – длина стороны симплекса между узлами i и j. (2L/3).

4. Вычислить интеграл 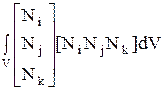, для симплексного треугольника площади A и толщины t. (At/2).

Лекция 5. ИНТЕРПОЛЯЦИОННЫЕ ПОЛИНОМЫ ДЛЯ ДИСКРЕТИЗИРОВАННОЙ ОБЛАСТИ

Необходимо включить каждый элемент в рассматриваемую область и выразить через глобальные координаты и глобальные узловые значения интерполяционные уравнения для отдельного элемента.

Общий вид интерполяционного полинома для элемента:

j^(e)=[N]{Ф}=[N_i^(e), N_j^(e), N_k^(e)…. N_r^(e)] {Ф_i^(e), Ф_j^(e), Ф_k^(e)…. Ф_r^(e)} (29)

r – число узлов элемента, верхний индекс – номер элемента.

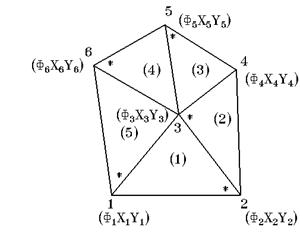
Рис. 4. Схема включения одного элемента в общую область.

Пусть имеем в области 5 элементов и 6 узлов. Узловые значения скалярной функции – это Ф₁,… Ф₆. Координаты глобальных номеров узлов – (X₁,Y₁)… (X₆,Y₆). Номер элемента написан на рис.4 в круглых скобках. Символ «*» стоит около 1 локального узла в каждом элементе – i «*»– j – k. Этот выбор совершенно произволен. Локальное движение номер узлов на каждом элементе идет против часовой стрелки (так принимается). Тогда для элемента № 1: i – 2; j – 3; k – 1. Для элемента № 2: i – 3; j – 2; k – 4.

Эти соотношения позволяют включить локальные номера узлов в глобальную систему нумерации. При этом фиксируются координаты узлов элемента. Тогда

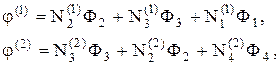(30)

Функции-формы на каждом элементе имеют свой вид и вычисляются по формулам

где 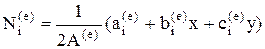и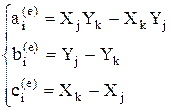

В результате все отдельные элементы объединяются в ансамбль. Из (30) имеем

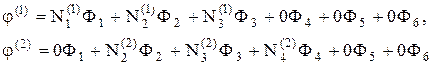(31)

Указанные в (31), уравнения можно записать в матричной форме:

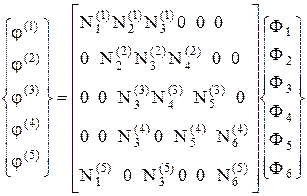(32)

Векторные величины

Аппроксимация векторных величин во всей области делается по аналогичным рассуждениям. Просто в каждом глобальном номер узла присутствует уже 2 скалярные узловые значения (для 2 измерений). Так, если узел №1, то имеем U₁ и U₂. В узле №2 имеем U₃ и U₄. и т. д. В итоге будет получено 12 узловых значений.

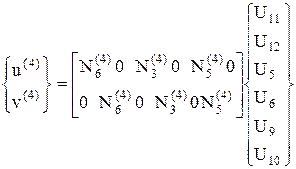(33)

Для уравнений (33) можно записать расширенную форму, с учетом всех узловых значений области.

Задачи

1. Определить соотношения, с помощью которых можно осуществить включение элементов в области, изображенные ниже. Отправной узел отмечен *.

а)	б)
в)	г)

2. Получите общие уравнения, определяющие элементы для областей, которые изображены выше, если в каждом узле 1 неизвестная.

Лекция № 6. РЕШЕНИЕ ЗАДАЧИ О ПЕРЕНОСЕ ТЕПЛА В СТЕРЖНЕ МКЭ. ПОСТАНОВКА ЗАДАЧИ

К закрепленному в стене стрежню подводится тепловой поток интенсивностью q. На свободном конце происходит конвективный обмен тепла. Коэффициент теплообмена h, температура окружающей среды T_c. Стержень теплоизолированный. Дифференциальное уравнение для распределения температуры внутри стержня:

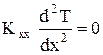(34)

с граничными условиями

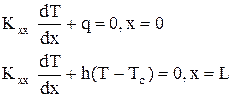(35)

где K_xx- коэффициент теплопроводности материала стержня; L – длина стрежня; q >0,если тепло отводится от стержня.

Задача (34)-(35) является исходной, для решения МКР. Уравнение (34) – УЧП параболического типа, стационарное. На левом конце стержня задано граничное условие Неймана, а на правом граничное условие смешанного типа. Разностная схема для решения подобных уравнений приводилась выше.

Можно использовать вариационный подход для решения данной задачи, связанный с минимизацией функционала.

Функционал, это определенный интеграл I, который принимает определенное значение в зависимости от вида подынтегральной функции F(x):

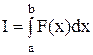. (36)

Основная задача вариационного исчисления – это отыскание такой функции F(x), чтобы при произвольном и бесконечно малом изменении этой функции δF(x) величина I оставалась неизменной. Рассмотрим функционал

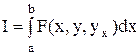. (37)

где x – независимая переменная; y(x) – переменная, зависящая от x; y_x – первая производная от y по x. Варьированием I вызывается изменением F(x)

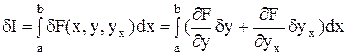. (38)

где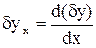

Интегрируем по частям второй член, получаем

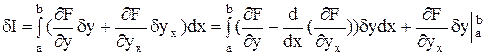. (39)

Функционал I принимает стационарное значение, если δI=0. Вариация δI=0, если равна нулю подынтегральная функция в (39) (поскольку вариация δy≠0)

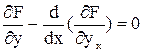и 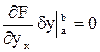(δy(a)= δy(b)=0). (40)

Следовательно, равенство нулю вариации функционала δI эквивалентно выполнению дифференциального уравнения

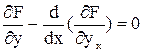
Пусть функционал имеет 3 независимых переменных F(s,t,l). Тогда

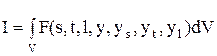. (41)

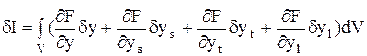. (42)

Интегрируем (42) по частям. Для второго слагаемого имеем

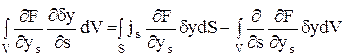(43)

где j_s – направляющий чкосинус нормали к поверхности S и оси Оs.

Аналогично для осей Оt и Ol.

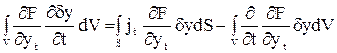
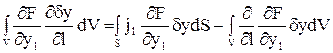
В итоге получаем

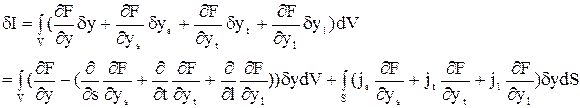(44)

Вариация функционала равна нулю, если равны нулю подынтегральные соотношения. Другими словами, функционал принимает стационарное значение, если

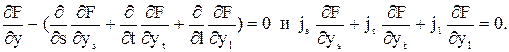(45)

Рассмотрим функционал вида

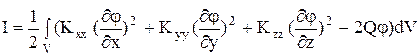. (46)

Найдем его вариацию и приравняем ее к нулю.

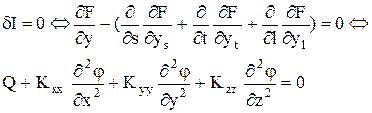(47)

Тогда, для случая одномерного стержня имеем следующий функционал

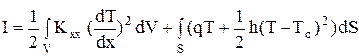. (48)

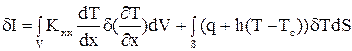. (49)

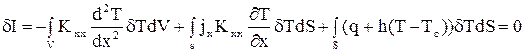. (50)

Равенство нулю его вариации эквивалентно выполнению ДУ (34) и граничных условий

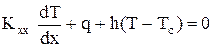. (51)

Минимум уравнения (48) эквивалентен исходной краевой задаче (34)-(35). Нужно провести минимизацию функционала (48) по заданным узловым значениям T_i. Любое распределение температуры, при котором функционал (48) становится минимальным, также удовлетворяет ДУ и является решением исходной задачи. Оба граничные условия (35) содержатся в (51), т.к. поверхностный интеграл в (48) должен быть разбит на два интеграла по каждой торцевой поверхности стержня.

Лекция № 7. РЕШЕНИЕ ЗАДАЧИ О ПЕРЕНОСЕ ТЕПЛА В СТЕРЖНЕ МКЭ. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ

Уравнение (48) является исходным для расчетов МКЭ. Минимизирует функционал I, используя множество функций элементов, каждая из которых определена на отдельном элементе через узловые значения T_i, которые нужно определить. Следовательно минимизация функционала проводится через оптимальный выбор узловых значений.

Разобъем стержень на 2 линейных элемента и будем иметь 3 узловые точки и 2 линейные интерполирующие функции. Температура внутри элементов находится с помощью формул

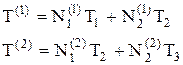(52)

где .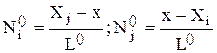

Исходный функционал распадается на 3 интеграла

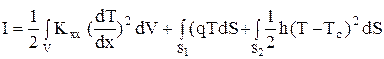, (53)

где S₁, S₂ – площади поверхностей, на которых заданы параметры q и h.

Вычисляем поверхностные интегралы. Для левого торца стержня задан тепловой поток. Имеем

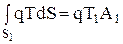. (54)

где A₁ – площадь сечения стержня, соответствующая первому узлу; функция T(x)=T₁ на левом краю первого элемента.

Для второго поверхностного интеграла имеем

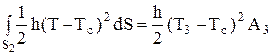, (55)

где А₃ и T₃ – площадь поперечного сечения и температура в третьем узле.

Для объемного интеграла имеем

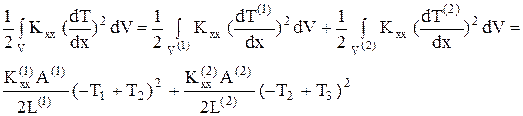.(56)

В результате получаем приближенное значение функционала, записанное через узловые значения для температуры

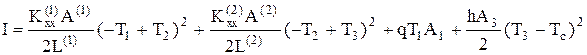(57)

Минимум функционала I определяется из системы уравнений

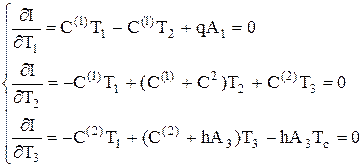(58)

где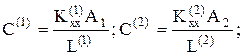

Или в матричном виде

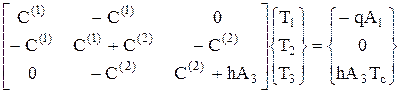, (59)

или в общем виде

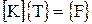, (60)

где K – глобальная матрица жесткости; T – вектор неизвестных; F – вектор глобальной нагрузки.

Интегрирование по элементам

Система уравнений для нахождения узловых значений (56) может быть получена другим путем, который более подходит для ЭВМ. Представим функционал I в виде суммы интегралов для 1-го элемента и второго элемента: I=I⁽¹⁾+I⁽²⁾. Тогда

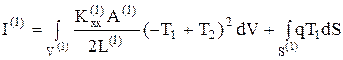(61)

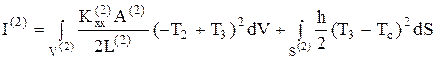(62)

Далее для минимизации всего функционала нужно минимизировать интегралы по каждому элементу, а потом их просуммировать, т. е.

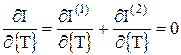(63)

Или

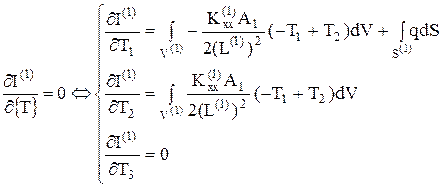(64)

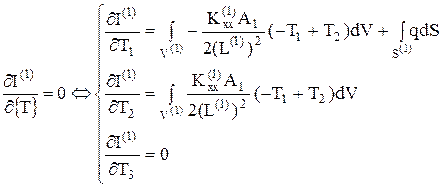(65)

Или в матричном виде

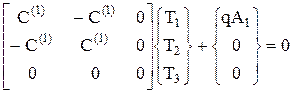(66)

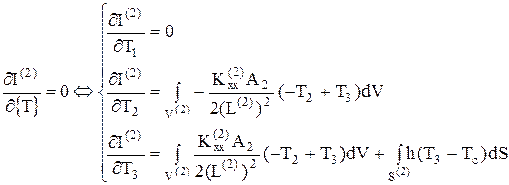(67)

Или в матричном виде

(68)

Суммирование матричных уравнений (66) и (68) приводит к уже полученной системе уравнений (59). С точки зрения машиной реализации последний метод создания итоговой системы линейных уравнений для определения узловых значений предпочтительнее.

ЗАДАЧА

1. Вывести уравнения для исходной задачи теплопроводности, если правый конец стержня теплоизолированный, а по боковой поверхности происходит конвективный теплообмен.

2. Вывести уравнения для исходной задачи теплопроводности, если правый конец стержня теплоизолированный, а по боковой поверхности подводится тепловой поток заданной интенсивности.

Лекция 8. РЕШЕНИЕ ЗАДАЧ ТЕОРИИ УПРУГОСТИ МКЭ

Путь решения – минимизация потенциальной энергии системы при отыскании узловых значений вектора перемещений. После нахождения узловых перемещений можно определить компоненты тензора деформаций и тензора напряжений.

Теорема. Из всех перемещений, удовлетворяющих кинематическим условиям, экстремальное значение потенциальной энергии сообщают те перемещения, которые удовлетворяют условиям равновесия.

Полная потенциальная энергия системы П:

П=П_д+П_с, (69)

где П_д – энергия деформации в теле; П_с – потенциальная энергия массовых сил и приложенных поверхностных сил.

Или

П=П_д-А_с, (70)

где А_с – работа внешних сил.

После разбиения области на элементы, имеем

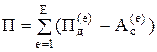. (71)

Осевое нагружение элемента конструкции

Пусть имеется упругий стержень длиной L, поперечного сечения A, который жестко защемлен с одной стороны. Под действием осевой силы P, которая приложена к свободному концу стержня происходит осевое перемещение x, которое линейно возрастает от 0 до 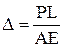,где E – модуль упругости стрежня, н/м².

Решим задачу МКЭ, используя 1 линейный КЭ, т.е.

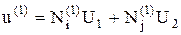, (72)

где U₁ = 0 на закрепленном конце стержня;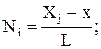

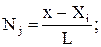
Тогда

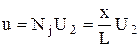. (73)

Потенциальная энергия системы определяется по формуле

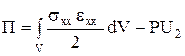, (74)

где первое слагаемое – энергия деформации стержня, а второе слагаемое – работа приложенной силы; s_xx – компоненты тензора напряжений, н/м²; ε_xx – компоненты тензора деформаций.

По закону Гука s_xx=Eε_xx. Тогда

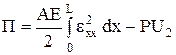, (75)

где .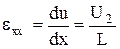

Или

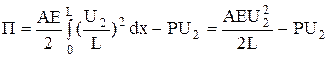, (76)

Минимизация потенциальной энергии П по узловому значению U₂ приводит

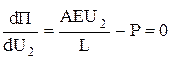. (77)

Или

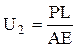, (78)

что совпадает с теоретическим значением.

Лирическое отступление 1

Что такое соционика?

	Направления исследований	Цели	Некоторые побочные эффекты (как результат длительного применения)
Соционика (наука это или нет неважно, важно, что как инструмент исследования мира это работает)	Определить свой ТИМ, оценить свои + и -	Наладить отношения с собой*	- развитие внимания - в сложных ситуациях происходит переключение с эмоций на анализ - моделирование ситуаций общения со временем переходит в привычку. А это практически программирование собственной судьбы.
Определить ТИМ партнера по общению, оценить его + и -	Наладить отношения с другими

*именно этап «наладить отношения с собой» некоторые соционики-пользователи по моим наблюдениям опускают. Это проявляется еще и в том, что люди стремятся, чтобы кто-то умный и авторитетный им определил их тип, рассказал как жить, а, заодно, убедил как-нибудь поубедительнее, что все у них с соционикой и вообще будет хорошо. Так вот, мой личный опыт говорит о том, что типировать себя нужно исключительно самостоятельно и это самый эффективный путь, если по жизни вы намерены развивать свою личную силу, а не чью-то. Кроме того, увлекаться кокетством в духе «ну, протипируйте еще и вы меня» не стоит. Это мое личное субъективное мнение.

Лирическое отступление 2

Теория Берна

Согласно теории Берна структура личности каждого человека независимо от его возраста состоит из трех зон или блоков (не путать с Фрейдом), условно называемых: Родитель, Взрослый, Дитя. По сути это три разных состояния психики, в которых человек может действовать. Примечательно, что человек может очень быстро «перемещаться» по этим трем уровням, а может «застрять» на одном из уровней. Вопрос в том насколько осознанно это происходит.

Зона	Проявление	Ключевые слова	Функции
Родитель Р	а) приказывает, контролирует, оценивает, осуждает; б) сочувствует, заботится, поощряет.	Такой порядок Так было всегда Должен Так надо Ничего не могу изменить	Система ограничений, ритуалов, правил, предписаний, исходящих извне. Личная ответственность отсутствует (виноваты правительство, начальство, соседи, муж/жена… только не я). Когда вам необходимо действовать как элемент системы, зона родителя (Р) может быть использована как страховочная, то есть эффективно (я действовал четко по инструкции).
Взрослый В	● сбор информации; ● анализ, проверка ее достоверности; ● принятие решений	Почему? Что именно? Каким образом?, согласен/не согласен, мое мнение и т.д. Я должен потому что мне интересно и поэтому Я ОТВЕЧАЮ ЗА РЕЗУЛЬТАТ	Объективная оценка реальности, конструктивное поведение, принятие самостоятельного, взвешенного и здравого решения. Руководство в своем поведении не эмоциями и желаниями (Д), не нормами (Р), а рациональностью, взвешенностью поступков, их обдуманностью, исходя из анализа ситуации. Это зона личной ответственности.
Дитя Д	а) потакание себе: действия необдуманны, импульсивны, непредсказуемы. б) угодить другому (чувство вины, страха перед наказанием, стыда). в) провокацирующее поведение: негативизм, капризность, возмущение, гнев. г) застенчив, стеснителен, обидчив.	Интересно Авось прокатит Хочу А мне по фиг Я тут не при чем	Стремление выйти за пределы ограничений, быть беззаботным, спонтанным. Эмоциональная несдержанность взрослого – это проявление детской позиции. Это зона риска, творчества, отдыха и «баловства». Личная ответственность отсутствует.

Подробнее о теории Берна можно прочитать тут: https://psy.gkbsviaz.ru/lim/obsheprof/psobshen/doc48_6a.html

Описание Значений карт: проявляется ситуативно, на уровне поведения, при решении тактических задач.

	Король	Дама	Рыцарь	Паж
Образы
Соционические функции	Экстраверсия Сенсорика	Интроверсия Сенсорика	Экстраверсия Интуиция	Интроверсия Интуиция
Ключевые слова	Статус, власть, авторитет, лидерство империя	Сохранение, наполнение, консерватизм, клан, монастырь, рутина	Уникальность, неповторимость, невозможное возможно, мозговой штурм	Самодостаточность, «свое кино», сам по себе
Направление деятельности	Стремление к захвату максимально возможного пространства, большего, чем есть, схватить здесь и сейчас	Стремление к удержанию захваченного, отграничение своего пространства от чужого, упорядочивание своего пространства	Стремление быть одновременно в прошлом, настоящем и будущем, обнаружить новую границу, создать новую форму, форма превалирует над содержанием	Сам в себе и для себя, стремиться отгородиться от внешнего мира. Для него не существует насилия, так как насилие над внутренним миром невозможно.
Символы	Расширяющееся пространство	Сжимающееся пространство	Расширяющееся время	Остановившееся время
Развитый вариант	Готов нести ответственность за других (свиту) и принимать оптимальные решения в кризисных ситуациях.	Готов наводить и сохранять порядок, ценности, традиции. В кризисные времена покровительствовать (принимать на баланс) другим ТИМам.	Готов обогащать идеями, оплодотворять почву, быть первопроходцем, первооткрывателем, умеет «наступать на горло своей песне», быть востребованным.	Готовность «выползать из своей раковины» и принимать участие в общем деле, работать над общей задачей
Неразвитый вариант	Деспот, не видит свою ограниченность, присвоение чужих заслуг, «голый король»	Зануда и педант, на его клумбе жить только по его правилам, «злая мачеха»	Склонен к эпатажу, выскочка, непризнанный гений, «белая ворона»	Аутсайдер, «человек в футляре»

Описание Значения мастей: п роявляется как фон, на уровне суждений, при решении стратегических задач.

	Посох	Кубок	Меч	Пентакль
Соционические функции	Рационал Этик	Иррационал Этик	Иррационал Логик	Рационал Логик
Социальная функция	Нравственность общества, обеспечение саморегуляции социума	Смазка общества, чтобы человек не чувствовал себя одиноким	Индивидуальное мастерство, создание новых алгоритмов	Командная работа, серийное производство, прибыль
Символы, стихия	Огонь	Вода	Воздух	Земля
Описание	Помешаны на правильно/неправильно. Суждения посохов направлены на соответствие установленным нормам морали и социальным правилам.	Суждения кубков ориентировано на индивидуальное отношение к человеку (нравится/не нравится), кажутся бесхребетными, так как всегда отражают других.	Парадоксальное мышление, неформальная логика, логика дзэн.	Ориентирован на формальную логику и жесткий алгоритм.
Мотивация	Режиссура, спектакль	Отражение, вдохновение	Спортивный интерес, новый алгоритм, эксперимент	Четкий механизм, все просчитано и предусмотрено
Кармическая задача (отработка судьбы по масти)	Нести ответственность, когда судите кого-то и обрекаете на наказание. Чтобы посох внутренне имел право судить и «выносить приговор», все страдания и испытания, на которые он обрекает другого, он сам должен пройти, пропустить через себя.	Нести ответственность за то, что отражаете. Быть искренними, держать психологическую дистанцию согласно ситуации.	Нести ответственность за эксперимент от а до я. Вместо жесткого контроля разобраться – что не так. Нужно понимать, что существует невозможное. Соизмерять цель и ресурсы.	Нести ответственность за адекватное распределение ресурсов и обязанностей в команде, чтобы все вышли в «+». Засеять и получить урожай.
Непроработанная масть	Навязчивые манипуляторы, интриганы, морализаторы и зануды.	Ненавязчивое манипулирование, капризность, фальшь.	Победа любой ценой, «рубит» все под ряд, тяжесть ненужной победы	Жлобство, получить прибыль и не поделиться.

Выводы:

1. Соционика – это скорее не наука, хотя и работает как инструмент научного познания мира. Соционика – на грани науки и искусства. Понимая основные принципы определения значений карт и мастей можно довольно глубоко исследовать личность, а также моделировать отношения и ситуации на разных уровнях. Символьная соционика при определении ТИМа не исключает, а напротив, позволяет включить такие аспекты личности как возрастные особенности, воспитание, мировоззрение, привычки, половую принадлежность и пр.
2. Определять значение карты удобно. Происходит это на уровне совмещения образов типируемого и К, Д, Р, П. Целое накладываем на целое и анализируем. Это как костюмчик одевать – сидит или не сидит. Можно определять методом исключений: точно не К и не Р, остается Д или П. То есть точно знаем, что интроверт, а сенсорику или интуицию определяем по дихотомическим признакам. Кроме того, можно придумать свой собственный способ совмещения символьной и знаковой соционики. Главное, чтобы вы получали удовольствие от процесса и удовлетворение от результата.
3. Масть хорошо проявляется при обсуждениях: обратите внимание на оценки людей и ситуаций.
4. Примечательно, что в состоянии Взрослого (по Берну) ТИМы не имеют явных проявлений. Человек в режиме Взрослого отдает себе отчет в деловой выгоде, в дельности ситуации, в трезвом состоянии человек осознанно распределяет свои тимные функции и способен проявляться и как К, и как Д, Р, П. Слабые стороны ТИМов проявляются только в режиме Р или Д, в режиме В их не будет видно.

Лирическое отступление 3

Информация к размышлению

Аспекты психологии как науки о душе	Цель	Результат	Примеры психо-технологий	Внимание, вопрос!
Я для других	Привести личность в соответствие нормам социума	Воспитание, укрепление, опредмечивание личности. Я такой, каким должен быть.	НЛП, гипноз, гештальт, психоанализ и пр.	А куда Вы поместили бы соционику? И почему?
Я для себя	Привести личность к трезвому взгляду на себя	Воспитание, укрепление, опредмечивание личности. Я такой, каким я. хочу быть.
Я и другие едины, Я как нечто отдельное отсутствует	Привести к трансформации человека через… частичное или полное разрушение личности	Выход за пределы личности. Я – какой угодно. Я проявляется соответственно ситуации.	Йога, боевые искусства, трансерфинг реальности (Зеланд), путь воина (Кастанеда)

P.S. Все изложенное не является истиной в последней инстанции. Это всего лишь субъективное мнение, основанное на моем личном опыте, тренингах Ольги Владимировны Негодиной и на изучении работ Сергея Савченко.

С уважением,

Наталия Шаститко.