Контрольные вопросы.
Рис.5.58.Фазовый портрет системы, оптимальный по быстродействию
Рис.5.57.Схема экстремального регулирования с запоминанием экстремума
Спуска
Рис.5.50.Схемы случайных стратегий
Раздел 5. Лекция 4. Основные принципы и виды алгоритмов функционирования систем автоматического управления технологическим объектом
Никулин Е.А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем. СПб.: БХВ-Петербург, 2004.
Филипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых знаний, 2001. С.113-326.
Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория Базовых Знаний, 2002. С.243-564.
Коганов В.Ю., Блинов О.М., Беленький А.М. Автоматизация управления металлургическими процессами. М.: Металлургия,!974. С.17-80.
Воронов А.А., Титов В.К., Новогранов Б.Н. Основы теории автоматического регулирования и управления. М.: Высшая школа, 1977. С.154-356.
Глинков Г.М., Косырев А.И., Шевцов Е.К. Контроль и автоматизация металлургических процессов. М.: Металлургия, 1989. С.94-143.
|
|
|
Майзель М.М. Автоматика и системы управления производственными процессами. М.: Высшая школа,1972. С.85-264.
Что представляют из себя линейные интегральные оценки качества регулирования?
Каким образом строится переходный процесс с прменением метода секущих?
Каким образом образом оценивается качество регулрования по ЛАЧХ?
Каким образом строится переходный процесс по вещественной частотной характеристике?
Что представляет из себя диаграмма Вышнеградского?
Что представляет из себя корневой метод определения качества регулирования?
Что такое показатель коелебательности?
Как реагирует система на гармонические входные параметры?
Как реагирует система на единичный импульс?
Литература по лекции 6.
1.Ульянов В,А., Леушин И.О., Гущин В,Н. Технологические измерения, автоматика и управление в технических системах. Ч.1. Н.Новгород: НГТУ, 2000. –С.7-77.
8.Методы классической и современной теории автоматического управления. Т.1 /Под ред. К.А. Пупкова. М.: МГТУ, 2004. С.150-179.
При автоматизации управления техническими процессами возникает необходимость в различных группах операций. К одной из таких групп относятся операции начала (включения) и прекращения (отключения) данной операции и перехода от одной операции к другой (переключения). Последняя группа операций рассматривается в теории переключающих устройств и конечных автоматов и отчасти в теории расписаний.
Для правильного и качественного ведения процесса некоторые из его координат – управляемые – должны поддерживаться в определённых границах или изменяться по определённому закону.
|
|
|
Другая группа операций управления связана с контролем за координатами с целью установления допустимых границ. Эта группа операций состоит в измерении значений координат и представлении результатов измерения в удобной для человека-оператора форме. Операции этой группы рассматриваются в теории автоматического контроля.
Третья группа операций управления – операции по поддержанию заданного закона изменения координат – изучается в теории автоматического управления.
Изменение координат в нормальном, желаемом процессе определяются совокупностью правил, предписаний или математических зависимостей, называемых алгоритмом функционирования системы. Алгоритм функционирования показывает, как должна изменяться выходной параметр ТОУ по требованию технологии, экономики или по другим соображениям. В теории автоматического управления алгоритмы функционирования считаются заданными.
Динамические свойства и форма статических характеристик вносят искажения6 действительный процесс будет отличаться от моделируемого (который, например, при тех же воздействиях имел бы место в безинерционных ТОУ). Поэтому требуемый закон управления G(τ), или алгоритм управления, не будет подобным алгоритму функционирования; он будет зависеть от алгоритма функционирования, динамических свойств и характеристик объекта. Алгоритм управления показывают, как должно изменяться управление G(τ), чтобы обеспечить заданный алгоритм функционирования. Алгоритм функционирования в автоматической системе реализуется с помощью управляющих устройств.
В основе используемых в технике алгоритмов управления лежат некоторые общие фундаментальные принципы управления, определяющие, как осуществляется увязка алгоритма управления с заданным и фактическим функционированием, или с причинами, вызвавшими отклонение. Используются три фундаментальных принципа, указанных выше.
Методы, или стратегии, оптимизации управления производственными процессами при нескольких аргументов функции качества и при нескольких соответственно каналах управления решают в сущности две задачи: 1)получение рабочей информации (определение отклонений от точки экстремума, частных производственных, градиента функции качества управляемого процесса); 2)использование этой информации – осуществление необходимых регулирующих (управляющих) воздействий для движения процесса к этой экстремальной точке. Следовательно, в стратегию оптимизации входит создание как поисковых (пробных) движений для решения первой задачи, так и рабочих (регулирующих) движений для выполнения второй.
Эти движения могут осуществляться как раздельно (т.е. последовательно во времени), так и совмещено. Управляющие системы с раздельными поисковыми и рабочими движениями вносят меньше искажений в управляемый производственный процесс, поскольку шаг поисковых движений обычно значительно меньше шага рабочих движений. Но в то же время, естественно, при раздельных поисковых и рабочих движениях быстродействие системы ниже, чем при совмещённых движениях.
Шаг поисковых движений обычно постоянен, а по характеру использования полученной информации различаются управляющие системы с постоянной и переменной величиной приращения регулирующих воздействий (с постоянным и переменным шагом рабочих движений. В обоих случаях направления приращений определяются знаками частных производных или градиента функции качества. При переменном шаге рабочих движений чаще всего его делают пропорциональным величине частной производной или градиента, в связи с тем что в обычных случаях чем дальше расположена точка от экстремального значения функции качества, тем больше абсолютные значения её производных и градиента. По мере приближения к экстремуму абсолютные значения производных и градиента снижаются и достигают нулю с переменной знака при переходе через экстремальное значение функции качества. Поэтому чем больше абсолютное значение частных производных и градиента функции качества, тем больше приращение можно давать регулирующему воздействию без риска перехода через экстремум функции качества.
|
|
|
Системы управления производственными процессами делятся на две основные группы: без моделирования ТОУ и с моделированием его. Системы управления без моделирования ТОУ не требует большого объёма априорной информации объекте, его статических и динамических характеристиках, а базируются на текущей информации об отклонениях от оптимального режима, о знаке и величине частных производных функции качества и её градиента. При этом поисковые движения осуществляются на ТОУ, что в какой-то мере искажает режим эксплуатации, приводит к потерям показателя качества, удлиняет процесс выхода на оптимальный режим и т.п.
Системы использующие математическую или физическую модель ТОУ, требуют большого объёма априорной информации об ТОУ, включая достаточно полное и подобное математическое описание либо физическую модель. Поисковые движения в этом случае осуществляется на математической или физической модели, что увеличивает точность и быстродействие системы, не вносит искажений в эксплуатационный режим ТОУ и т.п. Однако такая система сложнее и дороже.
Основными классификационными признаками систем оптимизации является случайность или детерминированность стратегии поиска. В случайных стратегиях направления поисковых движений в пространстве управляющих (регулирующих) воздействий задаются случайными, все направления считаются равновероятными, и на основе анализа этих случайных проб (либо других случайных процессов – флуктуаций и шумов) выбирается направление движения к экстремуму функции качества. В детерминированных стратегиях поиск осуществляется по определённым алгоритмам, заранее разработанным для движения к экстремуму функции качества.
|
|
|
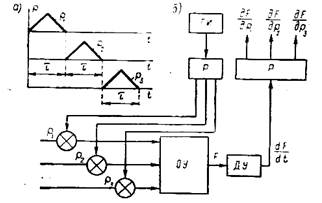 Рис.5.48.Схема измерения градиента функции качества способом производной по времени: а – цикл задания импульсов; б – схема; ОУ (ТОУ) – объект управления; ГИ – генератор импульсов; Р – распределители; ДУ – дифференцирующее устройство.
Рис.5.48.Схема измерения градиента функции качества способом производной по времени: а – цикл задания импульсов; б – схема; ОУ (ТОУ) – объект управления; ГИ – генератор импульсов; Р – распределители; ДУ – дифференцирующее устройство.
Рассмотрим три основных способов получения рабочей информации о назначении градиента функции качества (т.е. о направлении и характере изменения функции качества) или об отклонении рабочей точки этой функции от экстремального значения.
Первый метод получения текущего значения градиента функции качества основан на определении и суммировании частных производных функции качества по регулирующим воздействиям (в функции времени). Это путь называется способом производной по времени:
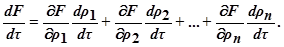
При этом создают определённые постоянные значения скоростей dρn/dτ (например, треугольными импульсами со значениями «+1» и «-1» в 1-й и 2-й половинах цикла) с их последовательным протеканием во времени (рис.5.48). Иначе говоря, в каждом интервале времени τ все производные регулирующих воздействий во времени (кроме одной, допустим с индексом q) равны нулю, и поэтому для этого интервала времени в дифференцирующем устройстве формируется dF/dτ = + 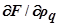 (для скорости «+1» и «-1»). При n импульсов по n каналам регулирования и определяются все компоненты градиента функции качества. Естественно, что в системе, использующей данный способ, должны находиться два синхронно работающих распределителя и один дифференцирующий элемент.
(для скорости «+1» и «-1»). При n импульсов по n каналам регулирования и определяются все компоненты градиента функции качества. Естественно, что в системе, использующей данный способ, должны находиться два синхронно работающих распределителя и один дифференцирующий элемент.
Недостатками рассмотренной системы являются:
· сравнительно высокий уровень помех, всегда сопровождающих операцию дифференцирования;
· относительно большая длительность цикла опроса всех аргументов, если их много.
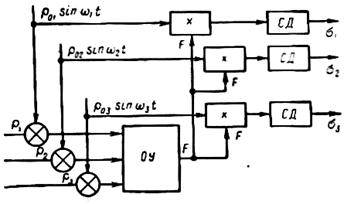 Рис.5.49.Схема измерения градиента функции качества способом синхронного детектирования: СД – синхронный детектор; ОУ- объект управления
Рис.5.49.Схема измерения градиента функции качества способом синхронного детектирования: СД – синхронный детектор; ОУ- объект управления
Второй, более сложным, но более совершенным, является определение градиента функции качества способом синхронного детектирования (рис.5.49). Основан на том, что к медленно меняющимся регулирующим воздействиям ρn принудительно добавляются специально создаваемые поисковые периодические (обычно гармонические) высокочастотные воздействия (по сравнению с периодами изменения координат φn с небольшими амплитудами: ρ01sinω1τ; ρ02sinω2τ … ρ0nsinωnτ.
Поисковые частоты ωn выбираются по числу аргументов, причём ни одна из этих частот не равна сумме или разности любой пары других частот. Этому условию отвечает, очевидно, выбор частот по закону нечётных чисел: ωq = (2m+1)ωo, где m = 1, 2,…, n. Вместе с тем для усреднения переменных величин назначается интервал времени, достаточно большой по сравнению с самой низкой как поисковой, так и разностной частотой. Такой режим называется квазистационарным и позволяет считать регулирующие воздействия ρn постоянными в пределах цикла поиска.
Функцию качества с достаточной для обычных инженерных расчётов точностью можно расположить в ряд Тейлора с использованием членов разложения, содержащих частные производные, включая второй порядок:
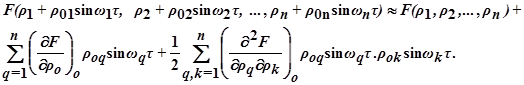
Сюда подставляются значения частных производных для исходного значения F(ρ1, ρ2, …, ρn).
Модулированная подобным образом функция качества поступает одновременно в параллельно подключенные синхронные детекторы по числу аргументов ρ. В каждый детектор синхронно с функций качества подаются опорные колебания одной из поисковых частот ω l. На выходе каждого детектора получается усреднённое произведение модулированной функции качества и опорного колебания ρ ol sinω l τ:
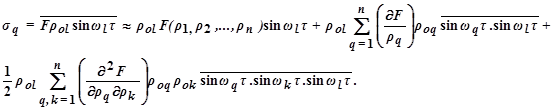
Как известно, усредненные синусы и их произведения при нечётном числе множителей равны нулю (из-за симметрии относительно оси абсцисс). Усредненное произведение из двух сомножителей
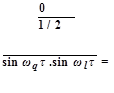
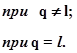
Следовательно, при соблюдении условия q = l на выходе всех синхронных детекторов одновременно образуются сигналы, пропорциональные частной производной функции качества для каждого соответственно регулирующего воздействия:
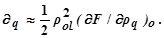
Следовательно, имея все компоненты, можно далее образовать градиент функции качества.
Третьим рассмотрим способ запоминания экстремума, который основан на том, что посредством поисковых движений изображающая точка перемещается в окрестности экстремума; при достижении функцией качества экстремального значения Fэ оно запоминается.
Текущее значение функции качества F можно выразить через Fэ, пользуясь предыдущим соотношение и учитывая, что в экстремальной точке все частные производные 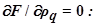
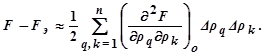
Частотные производные второго порядка вычислены для экстремального значения Fэ, а ∆ρq и ∆ρk – отклонении координат от экстремальных значений. Так как 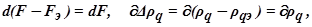 то из предыдущего выражения после дифференцирования по ρq найдём (учитывая, что под знаком суммирования имеются слагаемые и с q = k):
то из предыдущего выражения после дифференцирования по ρq найдём (учитывая, что под знаком суммирования имеются слагаемые и с q = k):
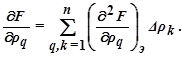
Следовательно,
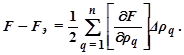
Например, при двух каналах регулирования (n = 2) получим:
 =
= 
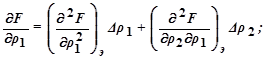
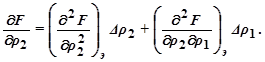
Следовательно,
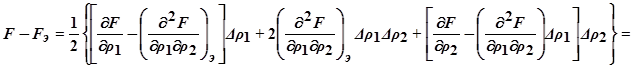
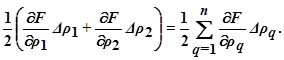
Таким образом, задавая отклонение ∆ρq и измеряя разность (F – Fэ), можно найти компоненты градиента функции качества. Выделить каждый из них из суммы 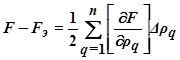 можно, в частности, пользуясь синхронными детекторами (рис.5.50). Каждый синхронный детектор (их устанавливают по одному на каждый канал регулирования) пропускает лишь одну компоненту (с заданной частотой) градиента функции качества. Задание экстремума Fэ хранится в запоминающем устройстве и сравнивается с текущим значением F в блоке сравнения. Изображающая точка в процессе поиска проходит через точку экстремума, когда разность (F – Fэ) = 0 и затем меняет свой знак, в результате чего изображающая точка начинает возвратное движение к экстремальному значению и т.д.
можно, в частности, пользуясь синхронными детекторами (рис.5.50). Каждый синхронный детектор (их устанавливают по одному на каждый канал регулирования) пропускает лишь одну компоненту (с заданной частотой) градиента функции качества. Задание экстремума Fэ хранится в запоминающем устройстве и сравнивается с текущим значением F в блоке сравнения. Изображающая точка в процессе поиска проходит через точку экстремума, когда разность (F – Fэ) = 0 и затем меняет свой знак, в результате чего изображающая точка начинает возвратное движение к экстремальному значению и т.д.
 Известно, что стратегии поиска бывают случайными и детерминированными. Из класса случайных стратегий поиска экстремума важнейшими являются два вида: чисто случайный поиск и поиск с использованием статистического градиента.
Известно, что стратегии поиска бывают случайными и детерминированными. Из класса случайных стратегий поиска экстремума важнейшими являются два вида: чисто случайный поиск и поиск с использованием статистического градиента.
Чисто случайный (гомеостатический) поиск осуществляется в трёх модификациях: с возвратом, с пересчётом и до изменения знака.
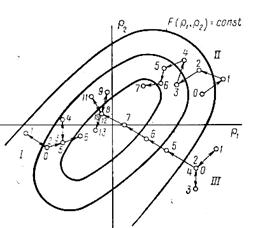
Чисто случайный поиск с возвратом заключается в следующем (рис.5.50, область 1). Из начального состояния 0 совершается первое пробное движении (0→1) в случайном направлении (все они равноправны). Полученные при этом изменение функции качества (определяется сравнением последующего значения с предыдущим) может быть направлено в нужную сторону (к желательному экстремуму), т.е приводит к успеху, либо в нежелательную сторону, не приводит к успеху. Если первое пробное перемещение приводит к успеху, то в том же направлении осуществляется первый пробный шаг. Затем опять в случайном направлении производится второе поисковое движение и т.д. Если же первое поисковое движение привело не к улучшению функции качества, а к её ухудшению, то рабочий шаг не осуществляется, система возвращается в исходное положение (по пути 0→1→2, 0), откуда снова начинается случайный поиск (2→3) и т.д.
Чисто случайный поиск с пересчётом (рис.5.50, область II) отличается от предыдущей стратегии лишь тем, что при поисковом шаге (0→1), ухудшающем функцию качества, система не возвращается в исходное состояние, а из положения 1 осуществляется второй случайный поиск (1→2), из положения 2-третий (2→3) также вне зависимости от успеха шага и т.д.
Чисто случайный поиск до изменения знака (рис.5.50, область III) отличается от стратегии с возвратом только тем, что, напав (после поисков в случайных направлениях 0→1→2, 0→3→4, 0) на нужное направление (4→5), дающее улучшение функции качества. Лишь теперь в точке 8 начнётся случайный поиск нового целесообразного движения системы (8→9→10, 8→11→12, 8) до нахождения нужного (12→13) или прекращения движения при достижении экстремума (в пределах зоны нечувствительности системы).
Поиск методом использования статистического градиента осуществляется следующим образом. Из начальной точки 0 осуществляется подряд m случайных одинаковых движений α в различных направлениях с синхронным вычислением приращения функции качества и образованием векторной суммы (статистического градиента):
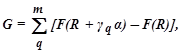
где R – вектор регулирующих воздействий; γq – единичные векторы, равномерно распределённые по всем направлениям пространства регулирующих воздействий.
Чем больше проб m, тем ближе направление вектора к направлению градиента функции качества (dF/dt = …-см. выше). Рабочий шаг осуществляется по направлению вектора G, т.е при больших m близко к направлению grad F.
Возможны две модификации рассматриваемой стратегии: при первой - методе статистического градиента – после каждого рабочего шага повторяется изложенная процедура поиска направления статистического градиента и второй рабочий шаг осуществляется по вновь вычисленному направлению и т.п. При второй модификации – методе статистического наискорейшего спуска – в вычисленном в первом цикле проб направлении вектора G производятся подряд шаги до тех пор, пока изменение функции качества. Затем только повторяется указанная выше процедура поиска направления статистического градиента и т.д.
Рассмотрим класс детерминированных методов поиска экстремума. Из них в настоящее время важнейшими являются четыре метода: Гаусса - Зайделя, градиента, наискорейшего поиска Опкон.
Метод Гаусса – Зайделя заключается в поочерёдном (по одному) изменении регулирующих воздействий (координат) при сохранении постоянства остальных. При этом выбирается направление изменения каждой координаты в сторону уменьшения абсолютной величины частной производной функции качества по этой координате, а движение осуществляется до положения, в котором 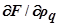 =0. Затем как же поступают со следующей координатой и т.д., включая последнюю координату ρq. После этого осуществляется второй такой же цикл по всем координатам, затем третий и т.д., до такого положения, при котором все компоненты градиента функции качества не станут меньше порога чувствительности системы.
=0. Затем как же поступают со следующей координатой и т.д., включая последнюю координату ρq. После этого осуществляется второй такой же цикл по всем координатам, затем третий и т.д., до такого положения, при котором все компоненты градиента функции качества не станут меньше порога чувствительности системы.
На рис.5.51, а ломанная I показывает применение рассматриваемого метода для двухмерного метода двухмерного процесса. На плоскости ρ1, ρ2 нанесены кривые равных значений функции качества F(ρ1, ρ2) = const. Первый шаг изменения координаты ρ1 (при ρ2 = const) производится до точки касания горизонтали 0-1 к кривой F(ρ1, ρ2) = const: в этой точке  =0. Затем при ρ1 = const меняется координата ρ2 по вертикали1-2 также до момента касания с кривой F(ρ1, ρ2) = const. Здесь
=0. Затем при ρ1 = const меняется координата ρ2 по вертикали1-2 также до момента касания с кривой F(ρ1, ρ2) = const. Здесь 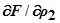 = 0. После этого снова изменяется ρ1 при ρ2) = const и т.д. В итоге изображающая точка перемещается по ступенькам - отрезкам горизонтальных вертикальных (ρ1 = const и ρ2 = const).
= 0. После этого снова изменяется ρ1 при ρ2) = const и т.д. В итоге изображающая точка перемещается по ступенькам - отрезкам горизонтальных вертикальных (ρ1 = const и ρ2 = const).
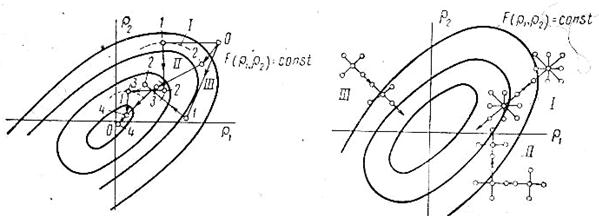 Рис.5.51.Схемы детерминированных методов Рис.5.52.Схемы поиска экстремума поиска экстремума: I-метод Гаусса – Зайделя; методом Опкон: I-исходная, II и III-
Рис.5.51.Схемы детерминированных методов Рис.5.52.Схемы поиска экстремума поиска экстремума: I-метод Гаусса – Зайделя; методом Опкон: I-исходная, II и III-
II-метод градиента; III-метод наискорейшего упрощенная
Метод градиента основан на определении мгновенных значений градиента функции качества путём измерения всех его компонентов (частных производных) и организации движения системы (непрерывно или шагами) по направлению, близкому к направлению этого градиента (рис.5.51, кривая II). Очевидно, что в идеальном случае в каждой точке пересечения траектории изображающей точки с поверхностью равных значений функции качества касательные взаимно перпендикулярны. Естественно, что путь движения изображающей точки в данном случае короче, чем при методе Гаусса – Зайделя.
Метод наискорейшего спуска близок к методу градиента и отличается тем, что движение направляется не по мгновенному значению градиенту функции качества, а по его значению в начале движения до момента обращения в нуль частной производной 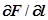 по направлению движения. В этой точке вновь определяется значение градиента, изображающая точка начинает перемещаться вдоль вектора опять до момента обращения в нуль
по направлению движения. В этой точке вновь определяется значение градиента, изображающая точка начинает перемещаться вдоль вектора опять до момента обращения в нуль 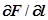 (уже по новому направлению градиента), после чего начинается третий этап движения (рис.5.51, ломанная III).
(уже по новому направлению градиента), после чего начинается третий этап движения (рис.5.51, ломанная III).
Следовательно, в отличие от метода градиента в данном случае изображающая точка движется не по кривой, а по взаимно перпендикулярным отрезкам прямых, так как частная производная 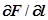 обращается в нуль в точке касания траектории изображающей точки к поверхности F = const, а grad F всегда нормален к поверхности F = const.
обращается в нуль в точке касания траектории изображающей точки к поверхности F = const, а grad F всегда нормален к поверхности F = const.
Метод поиска Опкон использует запоминание всех возможных комбинаций пробных движений, осуществляемых в начале каждого шага, начиная с начальной точки 0 (рис.5.52, область I). Число подобных комбинаций при n регулирующих каналов составляет N = 3n – 1; единица вычитается, поскольку нет пробного движения при отсутствии приращений по всем регулирующим воздействиям. Из опробованных комбинаций выбирается дающая наибольшее приращение ∆F функция качества (при поиске максимума) и в пространстве регулирующих воздействий в направлении выбранной комбинации даётся рабочий шаг, пропорциональный ∆F. При этом шаги всех регулирующих воздействий также пропорциональный ∆F, но с различными коэффициентами пропорциональности, зависящий от знака и величины пробного шага по данной координате. После окончания первого шага подобным же образом выбирается направление и осуществляется второй шаг и т.д. Естественно, что метод Опкон можно считать модификацией метода градиента.
Имеется две упрощенные схемы метода Опкон, уменьшающие число комбинаций для регулирующих воздействий (рис.5.52, области II и III).
Системы экстремального регулирования сложного многомерного объекта предназначены для создания совокупности координат φ1э, φ2э,…, φnэ регулируемого процесса, обеспечивающей экстремум заранее заданной функции (показатели качества) F(φ1, φ2,…, φn, t).
Подобные системы используют замкнутые цепи воздействия, причём рабочей информации служат рассогласования (отклонения, ошибки) текущих значений φ1 – φ1э,…, φ2 – φ2э,… φn,…, φnэ. При этом показатель качества зависит не только от собственных параметров ТОУ и регулируемых параметров, но и от неконтролируемых возмущений, не поддающихся предвидению и измерению, т.е. в итоге и от времени. Однако в большинстве случаев функция F(φ1, φ2,…, φn, t) во времени при постоянных регулируемых параметрах φ1, φ2,…, φn изменяется сравнительно медленно, что позволяет (для производственных процессов) считать показатель качества зависящим только от регулируемых координат, т.е. 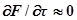 .
.
В этом случае условием экстремума дифференцируемой функции является равенство нулю всех её частных производных по регулируемых воздействиям ρ1, ρ2, … ρn:
 =
= 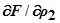 =…=
=…= 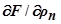
или равенство нулю градиента функции качества:
grad F = γ1  + γ2
+ γ2 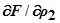 +
+
γn 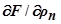 = 0,
= 0,
где γ1, γ2, …, γn – единичные векторы осей по направлениям пространства
регулирующих воздействий.
 Рис.5.53. Трёхмерный экстремальный холм
Рис.5.53. Трёхмерный экстремальный холм
Соответственно этому поиска экстремума бывают двух видов: последовательный поиск нулевых значений отдельных поиск нулевого значения градиента функции качества.
Система управления должна вырабатывать такие регулирующие воздействия (ρ1, ρ2, … ρn), совокупность которых создаёт требуемые экстремальные (минимум или максимум) значения функции качества при любых практически возможных сочетаниях возмущений и помех
Для простых (одномерных) процессов с одним регулируемым параметром φ и одним регулирующим органом, отрабатывающим одно регулирующее воздействие ρ, работа экстремального регулятора характеризуется (для обеспечения максимума F) следующей диаграммой (рис.5.53, так называемый экстремальный холм). На плоскости в координатах – возмущение ν, регулирующее воздействие ρ –нанесены кривые равных значений функции качества F. При данном возмущении (например, ν = 0,3) и возможных помехах функция качества может принимать любые значения в некоторых пределах (например, от 60 до 75%) в зависимости от величины регулирующего воздействия от величины регулирующего воздействия. Очевидно, что экстремальное значение функция F при данном ν принимает в точке, где  =
=  , т.е. где касательные к кривым постоянным F вертикальны (в данном случае при ρ=0,31; F =75%).
, т.е. где касательные к кривым постоянным F вертикальны (в данном случае при ρ=0,31; F =75%).
Соединив точки, соответствующие экстремума F, на кривых F = const, получим «гребень холма» О1О2, называемый оптимальной (или астатической) характеристикой ТОУ. Экстремальный регулятор и должен удерживать ТОУ (точнее, создавать надлежащее регулирующее воздействие) на этом гребне при любых возмущениях и помехах.
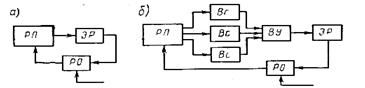 Рис.5.54.Схемы включения экстремум - регулятора
Рис.5.54.Схемы включения экстремум - регулятора
Рассмотрим схему экстремального регулирования одномерного процесса (рис.5.54). При этом возможны два случая: 1)когда регулируемая величина поддаётся непосредственному измерению; 2)когда регулируемая величина непосредственно не поддаётся измерению и для её нахождения требуется определённая вычислительная работа по некоторым замеряемым параметрам.
В первом случае значение регулируемого параметра непосредственно вводится в экстремум – регулятор Эр (рис.5.54, а), а во втором – измеряемые параметры процесса посредством воспринимающих блоков Вс вводятся в вычислительное устройство ВУ, которое в свою очередь выдаёт значение заданной функции (например, к.п.д.) в экстремум – регулятор (рис.5.54, б).
Таким образом, второй случай отличается от первого лишь включением между управляемым (регулируемым) процессом и экстремум – регулятором вычислительного устройства.
Простейшая схема системы экстремального регулирования для случая регулирования параметра, поддающегося непосредственному измерению, показана на рис.5.55.
 Рис.5.55.Схема экстремального регулирования с длительным устройством
Рис.5.55.Схема экстремального регулирования с длительным устройством
Информация о значении регулируемого параметра φ направляется воспринимающим блоком Вс в дифференцирующее устройство Дф, откуда сигнал k1 dφ/dt поступает в делительное устройство Дл. Туда же поступает сигнал k2 dρ/dt из второго дифференцирующего устройства Дф, в которое вводится координата ρ регулирующего органа РО.
В делительном устройстве осуществляется деление сигналов
k1 dφ/dt: k2 dρ/dt = k1 dφ/k2 dρ;
полученный сигнал направляется в реверсирующее реле РР. Если производная dφ/ dρ меняет знак, то это реле реверсирует работу исполнительного блока Ис. Лишь при экстремальном значении φ, т.е. когда dφ/dρ = 0, исполнительный блок находится в покое. Так как при равенстве нулю обеих производных (dφ/dt = dρ/dt = 0) их частное становится неопределённостью, то подобный регулятор должен обеспечить непрерывное изменение величины φ, т.е. его регулирующий орган РО должен работать по вибрационной схеме. Подобная схема может рассматриваться как схема может рассматриваться как следящая система, поддерживающая величину dφ/dρ на постоянном уровне (на нуле). Крупным недостатком рассматриваемой схемы является то обстоятельство, что при наличии ложных экстремумов (из – за помех) функции φ(ρ) регулятор может застабилизировать процесс на любом из них.
Схему, показанную на рис.5.55, можно несколько улучшить, исключив делительное устройство и введя вместо него специальный генератор треугольных импульсов, накладываемых на регулирующий орган (см. рис.5.48). Обычно выбирают угол наклона + 45о, т.е. создают постоянную скорость «+1» в первой половине импульса и «-1» - во второй его половине изменения регулирующего воздействия. При dρ/dt = + 1 получим dφ/dt = dφ/dρ dρ/dt = + dρ/dt, т.е. производная регулируемого параметра по времени (сигнал дифференцирующего устройства) равна производной регулируемого параметра по регулирующему воздействию (для первой половины периода поиска).
Более совершенна схема экстремум – регулятора показана на рис.5.56. В ней
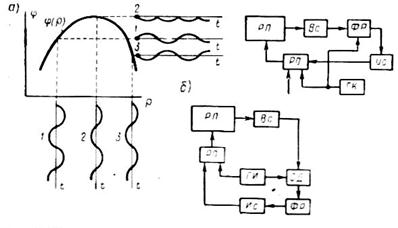 Рис.5.56.Схемы экстремального регулирования с перевёртыванием фазы: а – с фазочувствительным реле; б – с синхронным детектором
Рис.5.56.Схемы экстремального регулирования с перевёртыванием фазы: а – с фазочувствительным реле; б – с синхронным детектором
достижение экстремального значения функции φ(ρ) сигнализируется перевёртыванием фазы периодического колебания регулируемого параметра. Последнее создаётся периодическим колебанием регулирующего органа, накладываемы специальным генератором колебаний ГК на поступательное перемещение. Известно, что при периодическом колебательном возмущении выходная координата процесса также совершает периодические колебания с той же частотой, но с отставанием по фазе. Естественно, что при переходе регулируемым параметрам экстремального значения (за счёт поступательного перемещения регулирующего органа) колебание регулирующего органа в полупериоде с увеличением его координаты вызывает не увеличение регулируемого параметра (он уже на максимуме), а наоборот, его колебание в полупериоде с уменьшением параметра и т.д., т.е. перевёртыванием фазы колебаний регулируемого параметра. Соответственно этому в схему включается фазочувствительное реле ФР, управляющее исполнительным элементом Ис.
На рис.5.56, б показана ещё более совершенная схема, но и более совершенная схема, использующая вместо фазочувствительного реле синхронный детектор СД для определения знака и величины производной регулируемого параметра φ по регулирующему воздействию ρ. В детекторе перемножаются регулируемый параметр φ и опорный гармонический сигнал ρоsinωτ, выдаваемый генератором ГИ и направляемый также в регулирующий орган, Считаем, что частота опорного сигнала генератора (поисковая частота) весьма высока в сопоставлении с режимом изменения во времени регулируемого параметра; при этом можно положить, что за несколько периодов колебаний поискового сигнала значение регулируемого параметра изменяется лишь на слагаемое от поискового сигнала. Такой режим, как уже указывалось, называется квазистационарным.
Влияние поискового сигнала ρоsinωτ на регулируемый параметр можно с достаточной точностью учесть, применив разложение φ(τ) в ряд Тейлора (в окрестности значения φо до подачи сигнала поиска) с использованием первых трёх членов разложения:
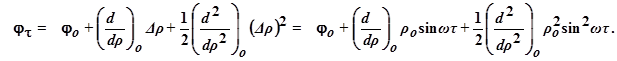
Здесь производные φ по ρ берутся при исходных значениях φ = φо и ρ до поступления поискового сигнала. На выходе синхронного детектора получим произведение
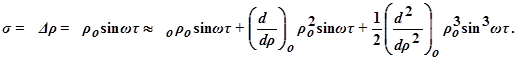
Математическое ожидание для обеих частей этого уравнения примет следующий вид:
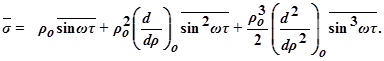
Как известно, для времени усреднения, в десятки раз превышающего период колебаний поискового сигнала, средние значения нечётных степеней синуса равны нулю (из-за симметрии относительно оси абсцисс). Средние значения квадрата синуса равно половине:
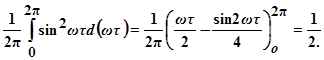
Следовательно, математическое ожидание
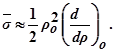
Таким образом, усреднённый сигнал синхронного детектора пропорционален производной регулируемого параметра по регулирующему воздействию; при этом по мере приближения к экстремальной точке сигнал 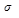 уменьшается по абсолютной величине, а при переходе меняет свой знак.
уменьшается по абсолютной величине, а при переходе меняет свой знак.
Зафиксировать экстремальное значение регулируемого параметра можно путём непрерывного или периодического определения знака приращения регулируемого параметра ∆φ: изменение этого знака с «+» на «- «соответствует переходу величины φ через максимум. Для этого (рис.5.57) сигнал воспринимающего элемента Вс, пропорциональный регулируемому параметру, поступает в запоминающее ЗУ и сравнивающее СУ устройства. Запоминающее устройство
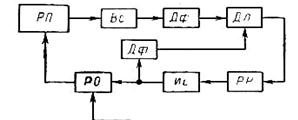
фиксирует нарастающие значения φ, однако, оно нечувствительно к снижению φ, т.е. запоминает максимальные значения величины φ = φэ. В сравнивающем устройстве сопоставляются сигналы запоминающего устройства и воспринимающего блока и вырабатывается воздействие, определяемое знаком разности этих сигналов. Допустим, что регулируемый параметр возрастает, при этом сигнал сравнивающего устройства остаётся неизменным. Когда регулируемый параметр достигнет максимального значения, то его последующая (текущая) величина окажется ниже этого максимума, зафиксированного в запоминающем устройстве. Соответственно этому измеряемое в сравнивающем устройстве приращение регулируемого параметра изменит свой знак и при достижении заданного по настройке значения (например, 1% от экстремального) вызовет надлежащий сигнал сравнивающего, поступающий в реверсивное реле, управляющее исполнительным блоком, и в запоминающее устройство для опорожнения памяти (пунктир на рис.5.57). Затем повторяется такой же цикл работы; иначе говоря, значение регулируемого параметра всё время колеблется вокруг своего максимального значения с допуском, зависящим от настройки.
Для некоторых простых объектов при пониженных требованиях к точности приближения к экстремальным значениям регулируемого параметра (при одномерном регулировании) принципиально возможно использовать, помимо рассмотренных кибернетических систем управления, и разомкнутые системы. В этом случае измеряется основное возмущение и на базе этой информации вырабатывается управляющее (регулирующее) воздействие для получения требуемых экстремальных показателей режима.
Для оптимизации производственных процессов часто используются комбинированные схемы. В них осуществляется измерение основного возмущения и использование этой информации для основных управляющих воздействий, с одной стороны, и, с другой, применение системы с обратной связью как для учёта влияния второстепенных возмущений, так и для компенсации недостаточной или ошибочной информации о динамических и статистических свойствах управляемого объекта и основного воздействия.
При применении принципа максимума к расчёту оптимальных по быстродействию САУ и САР используем функционал 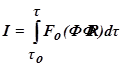 , в котором для рассматриваемого случая примем Fo(Ф, R)
, в котором для рассматриваемого случая примем Fo(Ф, R) 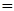 1.При этом I = τ1 – τ0, и минимальное значение функционала I соответствует минимальному времени перехода изображающей точки из положения А в В. Для этого случая В = 0, т.е. когда изображающая из положения А, характеризующего начальные условия, перемещается в начало координат, минимальное значение I характеризует минимальную длительность переходного процесса. Введём дополнительную систему их вспомогательных переменных ψ1, ψ2, …,ψn:
1.При этом I = τ1 – τ0, и минимальное значение функционала I соответствует минимальному времени перехода изображающей точки из положения А в В. Для этого случая В = 0, т.е. когда изображающая из положения А, характеризующего начальные условия, перемещается в начало координат, минимальное значение I характеризует минимальную длительность переходного процесса. Введём дополнительную систему их вспомогательных переменных ψ1, ψ2, …,ψn:
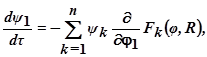
и вспомогательную функцию:
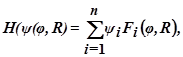
где ψ – вектор в n – мерном пространстве с компонентами ψ1, ψ2, …,ψn.
Связь между координатами φi и вспомогательными переменными ψi описывается уравнениями Гамильтона:
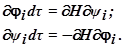 }
}
При фиксированных значениях ψi функция Н зависит от вектора управления R. Наибольшее значение Н обозначим через М(ψ, Ф) = Н(ψ, Ф, R).
Принцип максимума в рассматриваемом случае характеризуется следующим образом. При оптимальном управлении с вектором Rопт(τ) для перевода изображающей точки из положения А в В имеет место следующие обстоятельства:
1)при всех τ, заключенных в пределах τ0 < τ < τ1, характеризующих интервал времени протекания указанного процесса, функция Н(ψ, Ф, R) переменного R(τ) достигает при значении Rопт(τ) максимального значения М(ψ, Ф), а в конечный момент времени М[(ψ(τ1), Ф(τ1)] > 0;
2)если при этом ещё соблюдается уравнения Гамильтона то значения М(ψ, Ф) постоянно при переменном τ (τ0 < τ < τ1), что позволяет проверить соблюдение указанного условия для конечного момента времени τ1 пользуясь любым значением τ1 (τ0 < τ < τ1).
Рассчитаем оптимальную по быстродействию следящую систему второго порядка с управляющим воздействием в виде ускорения (точнее, движущего момента, создающего ускорение), ограниченного верхним значением по абсолютной величине. Передаточная функция линейной части системы
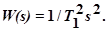 Следовательно, n=2 и r= 1.
Следовательно, n=2 и r= 1.
Р е ш е н и е. Для системы имеем
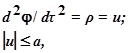 }
}
т.е. система второго порядка, для которой можно написать уравнения dφi/dτ = Fi(φ1, φ2,…, φn, ρ1, ρ2,…, ρr), i = 1, 2,…, n, приняв за выходные координаты: φ1 = φ и φ2 = dφ/dτ = ε:
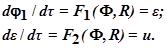 }
}
Следовательно, для вспомогательных функций (их две по числу координат) из 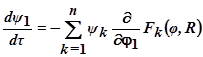 найдём:
найдём:
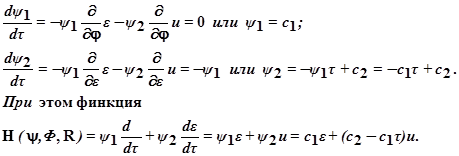
Для создания оптимального по быстродействию процесса нужно обеспечить максимальное значение функции Н(Ψ, Ф, R). Очевидно, что при этом второе слагаемое в выражении для неё должно быть положительным и наибольшим при имеющихся ограничениях. Естественно, что эти условия соблюдаются, если u = a sign(c2-c1τ).
В этом случае при τ<c2/c1 выражение в скобках положительно и ускорение u равно предельно допустимому а. При τ > c2/c1 происходит изменение знака бинома в скобках с положительного на отрицательный, следовательно, теперь ускорение u = - а, т.е. опять – таки равно предельно допустимому. Из – за линейности рассматриваемого бинома его знак меняется лишь один раз при изменении τ от 0 до 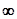 . Иначе говоря, оптимальность системы по быстродействию обеспечивается включением в неё идеального двухпозиционного реле. Следовательно, получаем нелинейную систему с кусочно – линейной характеристикой релейного звена.
. Иначе говоря, оптимальность системы по быстродействию обеспечивается включением в неё идеального двухпозиционного реле. Следовательно, получаем нелинейную систему с кусочно – линейной характеристикой релейного звена.
Рассмотрим изменение координаты φ на обоих работы системы. При 0 < τ < c2/c1
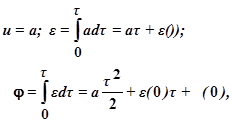 }
}
т.е. скорость ε нарастает линейно, а координата φ – по параболе.
Найдём дифференциальное уравнение фазовых траекторий из 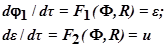 делением производных обеих координат друг на друга:
делением производных обеих координат друг на друга: 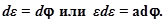
После интегрирования 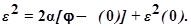
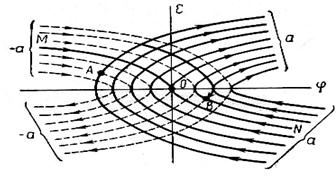
т.е. фазовые траектории представляет собой параболы, зависящие от начальных условий (рис.5.58).
Аналогично для второго этапа, когда с2/с1<τ<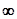 , найдём (отсчёт времени ведём от начала второго этапа, т.е с момента τ=с2/с1):
, найдём (отсчёт времени ведём от начала второго этапа, т.е с момента τ=с2/с1):
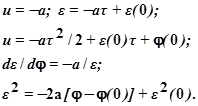 }
}
т.е. для второго этапа имеем семейство парабол (кривые для +а сплошные, а для –а - пунктирные).
Из фазовой диаграммы видно, что переход из любой точки А фазовой плоскости в другую точку В осуществляется по двум отрезкам двух парабол. Для перехода из любой точки А в начало координат (т.е. в состояние равновесия) вторыми этапами движения будут служить отрезки параболы МN, проходящей через начало координат. Иначе говоря, парабола MN служит в этом случае линией переключения.
Очевидно, что уравнение параболы MN имеет следующий вид («+» для второго и «_» для четвёртого квадрантов): 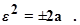
Инвариантными системами называются САУ, в которых обеспечивается полная или частичная независимость каких-либо регулируемых параметров от действующих возмущений. Иначе говоря, в инвариантах системах осуществляется полная или частичная компенсация внешних возмущении в процессе их образования. Для этого обычно предусматривается самонастройка системы, учитывающая вид, значение и место приложения внешних воздействий и соответственно меняющая динамические характеристики системы.
Рассмотрим одну из основных задач – обеспечение селективной инвариантности постоянного значения какого – либо регулируемого параметра (допусти φi) при действии внешнего возмущения νj. При m регулируемых параметрах линейной или линеаризованной системы её динамику можно описать системой линейных или линеаризованной системы её динамику можно описывать системой линейных уравнений относительно изображений регулируемых параметров и возмущений (на основе аддитивности реакции системы на возмущения):
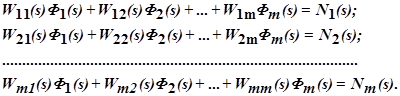
Будем искать условие независимости параметра φ1(τ) = L-1[Ф1(s)] от возмущения ν2(τ)=L-1[N2(s)]. Допустим, что последнее изменилось на ∆N2(s). Естественно, что при этом остальные параметры 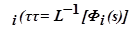 приобретут приращение
приобретут приращение 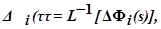 кроме параметра φ1(τ), который по условию останется неизменным. Следовательно, из последней системы получим
кроме параметра φ1(τ), который по условию останется неизменным. Следовательно, из последней системы получим
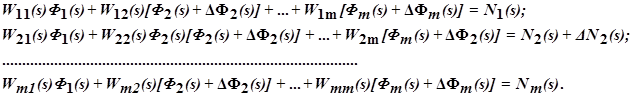 После построчного вычитания предыдущей системы из последней получим новую систему m линейных уравнений, в которой будут участвовать только m приращений (m – 1) параметров из одного возмущения:
После построчного вычитания предыдущей системы из последней получим новую систему m линейных уравнений, в которой будут участвовать только m приращений (m – 1) параметров из одного возмущения:
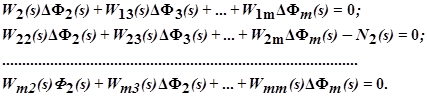
Если считать ∆N2(s) неизвестным, то последняя система становится однородной относительно всех m приращений. Её решение отличны от тривиального (когда все m неизвестных равны нулю) лишь тогда когда определитель, составленный из коэффициентов уравнений, равен нулю:
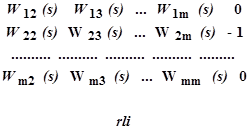 .
.
В определителе отсутствуют элементы, содержащие члены со вторым индексом «1» [по индексу постоянного параметра φ1(τ)]. В последнем столбце определителя все элементы, кроме второго, равны нулю. Поэтому после разложения определителя по этому столбцу найдём, как исходное условие независимости φ1(τ) от ν2(τ), равенство нулю минора ∆2m, полученного после удаления второй строки (по индексу возмущения) и не содержащего элементов, которые были первыми в левых частях уравнений
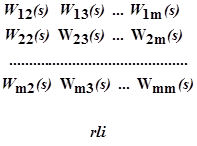 .
.
В общем случае, если нужно найти условие независимости параметра φi(τ) от возмущения νi(τ), из определителя
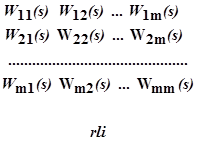
удаляются j-я строка и i-й столбец, а полученный минор приравнивается нулю.
Кроме рассмотренного случая селективной инвариантности имеются самонастраивающиеся системы абсолютно инвариантные (по всем параметрам), системы с переменной степенью инвариантности, параметрические системы, обеспечивающие компенсацию изменений параметров самой системы, и т.п. Во всех этих случаях, кроме основного контура автоматического регулирования, имеется дополнительный контур (иногда даже не один) для самонастройки на инвариантность.
Одной из важнейших задач, решаемых при использовании инвариантных систем, является исключение динамических ошибок при работе следящей системы, например при обеспечении требуемых соотношений подачи сырья и материалов для обработки, когда подача материалов должна строго следить за поступлением сырья при переменной её величине (во времени). Следовательно, в этом случае возмущением является изменение во времени поступления сырья, а независимой от этого обстоятельства должна быть неизменность нулевой ошибки подачи материалов как функции подачи сырья.
Универсальным способом описания процессов автоматического управления являются их алгоритмы, т.е. совокупность преобразований, математических действий и логических условий, действующих в определённом порядке. Алгоритм может быть описан словами общеизвестной и специальной терминологии и обычными математическими символами. В последние года в связи с быстрым внедрением в технологию управления вычислительных устройств широко применяется более удобные и экономичные логические схемы алгоритмов, в частности предложенные А.А. Ляпуновым. При этом любой алгоритм рассматривается состоящим из операторов и предикатов.
Операторы описывают физические и математические преобразования и действия, осуществляемые в процессе управления. Например, «повернуть рукоятку 7 на два оборота по часовой стрелке», «возвести в квадрат произведение сигналов, полученных по каналам 3 и 5», и т.д. Операторы обозначаются заглавными латинскими буквами А, В, С, В,…, или А(x~y), B(z~u), C(y~z) и т.д., где в скобках указывается входная и выходная координаты оператора. Последовательное осуществление операции (срабатывание операторов), не ограниченное какими-либо условиями, обозначается произведением символов операторов. Например, АСD – последовательное осуществление операций, описываемых операторами А, С, и D/
Предикаты – логические условия, указывающие на ограничения, накладываемые на осуществление тех или иных операций (на срабатывание операторов). Например, оператор В срабатывает лишь тогда, когда выходная координата оператора А равна единице, или оператор В не срабатывает, если в него поступает сигнал без постоянной составляющей. Логические условия обозначаются строчными латинскими буквами: p, q, r …. Иногда рядом с символом логического условия в скобках указываются его содержание, например p(х>2), т.е условие сводится к тому, что величина х должна быть больше двух. Выполнение условия обычно кодируется «1», а нарушение –«0». Символ логического условия, расположенный перед символом оператора, например рА, указываеь на то, что сначала проверяется выполнение условия р, а затем, если оно выполнено, уже срабатывает оператор А. Если символ логического условия располагается между символами операторов, например ВрСD, то после срабатывания оператора В проверяется условие р и, если выполнено, срабатывают последовательно операторы С и D.
При более сложных сочетаниях операторов и логических условий, при необходимости повторных срабатываний, при кольцевании информации и т.д. используются вертикальные стрелки с верхними индексами. Стрелка, направленная верх с цифрой сверху (например, 3), указывает на начало (номер исходной точки) передачи информации. Стрелка, направленная вниз с цифрой сверху, указывает конец передачи информации из начальной точки передачи с этим номером. Стрелка, направленная вверх и расположенная перед символом логического условия, показывает направление информации в случае неудовлетворения условия. Стрелка, направленная вниз и расположенная перед символом оператора, указывает на поступление в него информации из точки с номером, указанным на стрелке. Если логическое условие выполняется, то информация последовательно проходит из оператора перед символом условия в оператор за символом условия, а стрелки при этом не учитываются.
Для иллюстрации сказанного рассмотрим логическую схему:
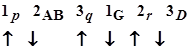 .
.
Состоящую из четырёх операторов ABCD и трёх логических условий p, q и r. Каждое из них может быть в двух состояниях: «1» (выполнено) или «0» (не выполнено). Всего возможно 23=8 алгоритмов (порядков работы) системы, указанных в табл. 5.2 (часть их может совпадать).
Таблица 5.2
Варианты алгоритмов к схеме
| Условия | Алгоритмы | Условия | Алгоритмы | ||||
| p | q | r | p | q | R | ||
| СABD CD CADCADC CD | ABD ABD ABCABCA ABCD |
Для случаев 010 и 110 путь информации замыкается внутри системы и выходной оператор D не срабатывает.
Если нужно обозначить передаваемую в систему информации, составляют развёрнутую схему с указанием передачи информации х на вход оператора А или В символом Г (х→А) или Г (х→В) и преобразования, осуществляемого в операторе. Например, развёрнутая логическая схема
1 1
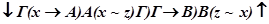
означает, что информация х поступает в оператор А, преобразуется в нём в z, подаётся в оператор В, где преобразуется в х и возвращается на вход оператора А.
Широко распространена запись алгоритмов с заменой стрелок знаками переходов информации. Если после выполнения логического условия срабатывает записанный дальше рядом оператор, то знак перехода не ставится. Если же после выполнения логического условия (например, q) должен срабатывать оператор (например, В), расположенный в алгоритме не сразу за этим условием, то после последнего (q) пишется  c некоторым номером сверху, который повторяется снизу под знаком
c некоторым номером сверху, который повторяется снизу под знаком  (правым) перед оператором (В), срабатывающим при выполнении условия (q). Если же при невыполнении условия (q) ставится знак
(правым) перед оператором (В), срабатывающим при выполнении условия (q). Если же при невыполнении условия (q) ставится знак  (левый), перед оператором (D) такой же, как и прежде, знак
(левый), перед оператором (D) такой же, как и прежде, знак  . Если после логического условия (q) нужны оба знака
. Если после логического условия (q) нужны оба знака 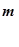 и
и  (т.е. требуется указать путь информации в случае как выполнения, так и не выполнения этого условия), то ставится знак
(т.е. требуется указать путь информации в случае как выполнения, так и не выполнения этого условия), то ставится знак  . Передача информации после одного оператора (например, В) в другой (например, D), не следующий непосредственно за первым непосредственно за первым, обозначается знаками
. Передача информации после одного оператора (например, В) в другой (например, D), не следующий непосредственно за первым непосредственно за первым, обозначается знаками  и
и  , стоящий после оператора В и перед оператором D.
, стоящий после оператора В и перед оператором D.
На последовательность записанных рядом операторов и логических условий стоящие между ними знаки перехода не влияют.
Прекращение процесса после какого-либо логического условия обозначается знаком останова s. Тождественно ложное условие (которое никогда не выполняется) обозначается знаком ω.
 2014-02-05
2014-02-05 716
716






