Лекция 2.
В.М. Полтерович. Базовые модели макроэкономики
Equivalence at Text Level
Equivalence at Sentence Level
It occurs: a) in phraseology – two is company, three is none – третий лишний; b) in orders and regulations – keep off the grass – по газону не ходить.
It is usual in the translation of poetry as seen in the translation of William Blake’s stanza by S. Marshak.
1. To see a World in a Grain of Sand,
2. And a Heaven in a Wild Flower,
3. Hold Infinity in the palm of your hand,
4. And Eternity in an hour. (W. Blake, Auguries of Innocence)
4. В одно мгновенье видеть вечность,
1. Огромный мир – в зерне песка,
3. В единой горсти – бесконечность
2. И небо – в чашечке цветка.
The translation by S.Marshak may be regarded as excellent. The text as a unity is reproduced most fully and this conception of unity justifies the change in the order of the lines within the stanza.
A strict observance of equivalence at all levels ensures a similar reaction on the part of the S and T language receptors and can be achieved by means of functional substitutions.
Рамсея (формулировка)
Фрэнк Рамсей (Frank Ramsey, 1903-1930) - английский математик, логик, философ и экономист, работавший в Кембридже и за свою короткую жизнь успевший сделать необыкновенно много. В частности, он написал три работы по экономике, все три стали классическими. Работа по теории роста (A mathematical theory of saving), где была предложена одна из базовых моделей макроэкономики, опубликована в 1928 г.
|
|
|
В этой и следующих лекциях мы изучим ее современную версию в двух вариантах –централизованном и децентрализованном.
В централизованном варианте модели Рамсея репрезентативный агент (или плановый орган) максимизирует дисконтированную полезность на бесконечном интервале времени.

(1) 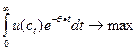
(2а) 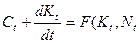 )
)
(3а) 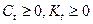
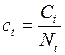 ,
, 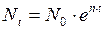 .
.
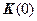 = К0 - задано.
= К0 - задано.
Здесь 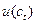 - мгновенная полезность (instantaneous utility function),
- мгновенная полезность (instantaneous utility function),
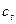 - поток душевого потребления,
- поток душевого потребления,
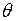 - дисконт полезности (rate of time preferences),
- дисконт полезности (rate of time preferences),
F (K,N) – неоклассическая производственная функция, со всеми перечисленными в Лекции 1 свойствами, – это выпуск, который делится на потребление и инвестиции.
Каким образом происходит это деление, заранее не известно; этим модель принципиально отличается от модели Солоу. Деление выпуска на потребляемую и накапливаемую часть происходит таким образом, чтобы оптимизировать функционал (1).
Репрезентативный потребитель оценивает потребление с помощью функции полезности u. Полезность, полученная в разные промежутки времени, имеет разную ценность; межвременное предпочтение задается с помощью коэффициента (нормы дисконта полезности) 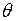 .
.
Т.о., агент максимизирует дисконтированную сумму полезности на бесконечном временном интервале при естественном технологическом ограничении. Если начальное значение капитала К0 задано, то при выполнении определенных предположений, можно найти единственную оптимальную траекторию.
Предполагается, что функция F(K, N) задает чистый выпуск, равный валовому выпуску G(K, N) за вычетом амортизации.
|
|
|
В модели мы считаем, что амортизация пренебрежимо мала, либо что она уже фактически исключена из выпуска:
F(K, N) = G(K, N) - 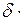 K,
K,
где 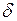 – норма амортизации.
– норма амортизации.
Отметим, что прибавление линейного члена не нарушает линейную однородность. Все основные свойства производственной функции сохраняются (кроме поведения на бесконечности, что не меняет выводов).
Таков централизованный вариант модели Рамсея. Обсудим подробнее, о чем здесь идет речь.
Замечания:
1. Если полезность u измерена в деньгах, то возможным значением 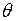 оказывается действующий процент. В эмпирических исследованиях нелегко выявить, какую именно процентную ставку надо принимать во внимание, т.к. их существует много. В теории мы считаем, что
оказывается действующий процент. В эмпирических исследованиях нелегко выявить, какую именно процентную ставку надо принимать во внимание, т.к. их существует много. В теории мы считаем, что 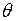 , вообще говоря, отлично от ставки процента.
, вообще говоря, отлично от ставки процента.
2. Функционал – это дисконтированная полезность одного члена общества. Т.о., мы предполагаем, что все члены общества одинаковы.
Можно было бы максимизировать интегральную дисконтированную полезность всех членов общества:
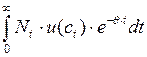 .
.
Т.к. предполагается, что Nt растет постоянным темпом, то при 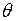 > n такая постановка эквивалентна предыдущей, поскольку интегральная дисконтированная полезность равна
> n такая постановка эквивалентна предыдущей, поскольку интегральная дисконтированная полезность равна
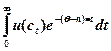 .
.
3. Функции полезности нам неизвестны. Почему тогда интересно изучать такого рода модели?
Во-первых, нас интересуют качественные заключения, которые не зависят от и. Мы стараемся выявить качественные особенности изучаемых траекторий.
Во-вторых, и, 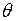 и F могут быть найдены по статистическим данным. Предположим, что мы верим, что реальная траектория является оптимальной для некоторых и,
и F могут быть найдены по статистическим данным. Предположим, что мы верим, что реальная траектория является оптимальной для некоторых и, 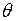 и F. Функции и, F можно задать параметрически, затем найти оптимальную траекторию в общем виде, либо выписать соотношения, ее характеризующие. После этого подбираются такие значения параметров, для которых расчетная траектория выпуска, капитала и потребления наилучшим образом аппроксимирует наблюдаемую траекторию. Если модель неплохо описывает прошлое, то можно надеяться, что с ее помощью можно также прогнозировать будущее.
и F. Функции и, F можно задать параметрически, затем найти оптимальную траекторию в общем виде, либо выписать соотношения, ее характеризующие. После этого подбираются такие значения параметров, для которых расчетная траектория выпуска, капитала и потребления наилучшим образом аппроксимирует наблюдаемую траекторию. Если модель неплохо описывает прошлое, то можно надеяться, что с ее помощью можно также прогнозировать будущее.
Почему, однако, можно предполагать, что экономика развивается оптимальным образом?
Во-первых, мы увидим, что модель допускает децентрализованное представление. Соответствующие траектории генерируются не путем отыскания оптимального плана, а путем взаимодействия участников на рынке. Идеальная конкурентная рыночная экономика генерирует оптимальные траектории.
Во-вторых, можно считать, что модель (1)-(3а) претендует на описание движения, а не на описание мотивов. Агенты не обязательно осознают задачу (1)- (3а). Предполагается, что реальное движение может быть представлено как результат оптимизации функционала (1) (сравните с вариационными принципами теоретической механики).
В ряде случаев модель можно модифицировать так, чтобы учесть несовершенства рынка.
4. Функционал (1) не инвариантен относительно произвольного монотонного преобразования функции и(с). Он инвариантен только относительно линейного преобразования.
5. В задаче отсутствует ограничение на знак производной 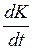 . Это означает, что в любой момент капитал можно частично "проесть". Однако овеществленный капитал не всегда легко обратить в потребление. Например, не всегда просто продать оборудование иностранному инвестору. Если снять это весьма серьезное предположение, то модель становится более сложной.
. Это означает, что в любой момент капитал можно частично "проесть". Однако овеществленный капитал не всегда легко обратить в потребление. Например, не всегда просто продать оборудование иностранному инвестору. Если снять это весьма серьезное предположение, то модель становится более сложной.
Приступаем к исследованию модели.
Введем удельные переменные:
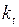 =
= 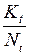 ,
,
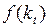 =
= 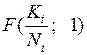
(2) 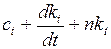 =
= 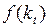
(3) 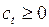 ,
, 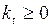 .
.
В дальнейшем считаем, что функция 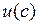 является вогнутой и гладкой,
является вогнутой и гладкой, 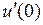 =
= 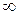 . Примером такой функции является
. Примером такой функции является 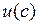 =
= 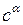 , 0
, 0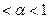 .
.
Можно заметить, что условия (3) в действительности не нужны. Если их отбросить, то решение не станет отрицательным, поскольку функции 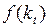 и
и 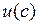 имеют бесконечные производные в нуле.
имеют бесконечные производные в нуле.
Условия оптимальности задачи (1)-(3).
|
|
|
Применим к нашей задаче принцип максимума. В данном случае функция Гамильтона имеет вид
(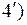
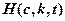 =
= 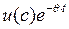 +
+ 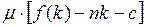 .
.
Согласно принципу максимума, имеем:
(5) 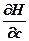 = 0.
= 0. 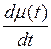 = -
= - 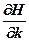 .
.
(6) Условия трансверсальности:
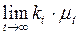 = 0.
= 0.
Условия (2), (3), (5), (6) являются необходимыми и достаточными условиями оптимальности.
Смысл двойственных переменных.
Двойственная переменная характеризует изменение максимального значения 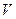 функционала (1) при малом изменении начального капитала:
функционала (1) при малом изменении начального капитала:
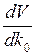 =
= 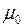 .
.
Значение капитала 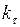 на оптимальной траектории в произвольный момент t можно рассматривать как начальную точку, поэтому
на оптимальной траектории в произвольный момент t можно рассматривать как начальную точку, поэтому
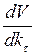 =
= 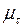 .
.
Для того, чтобы прояснить смысл условия трансверсальности, докажем, что принцип максимума достаточен для оптимальности.
Пусть 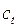 ,
, 
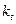 - траектория, удовлетворяющая принципу максимума,
- траектория, удовлетворяющая принципу максимума, 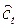 ,
, 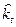 - произвольная траектория.
- произвольная траектория.
Поскольку функция Гамильтона (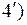 достигает максимума по c в каждой точке оптимальной траектории, имеем
достигает максимума по c в каждой точке оптимальной траектории, имеем
(а) 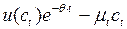
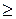
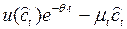 для
для 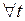 .
.
Введем обозначения 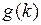 =
= 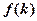 -
- 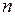
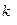 ,
, 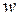 =
= 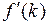 -
- 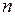 =
= 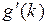 .
.
Поскольку 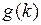 вогнута
вогнута 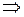
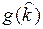
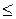
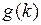 +
+ 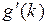 (
(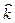 -
- 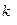 ), значит,
), значит,
(в) 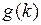 -
- 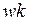
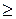
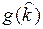 -
- 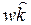
Умножим (в) на 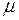 и сложим с (а), затем проинтегрируем:
и сложим с (а), затем проинтегрируем:
(с) 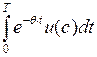 -
- 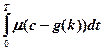 –
– 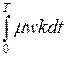
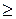

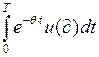 –
– 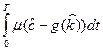 –
– 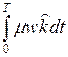 .
.
Исходный баланс:
(d) 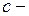
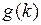 = –
= – 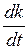 .
.
(e) 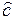 –
– 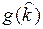 = –
= – 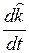 .
.
Воспользуемся уравнением (5), входящим в принцип максимума.
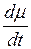 = -
= - 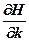 = –
= – 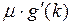 = –
= – 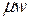 . Интегрируя по частям, имеем:
. Интегрируя по частям, имеем:
(f) – 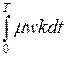 =
= 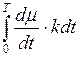 =
= 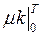 –
– 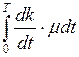
Аналогичное соотношение получается, если вместо 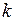 поставить
поставить 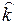 (
(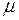 и
и 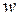 те же самые). Рассмотрим (с) и учтем выражения, которые мы получили. Вначале в (с) подставляем (d) и (е), потом используем (f) и его аналог для
те же самые). Рассмотрим (с) и учтем выражения, которые мы получили. Вначале в (с) подставляем (d) и (е), потом используем (f) и его аналог для 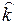 .
.
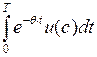 +
+ 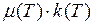 -
- 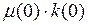
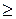
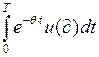 +
+ 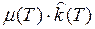 –
– 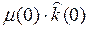 .
.
Заметим, что 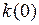 =
= 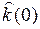 , т.к. начальные условия одинаковы.
, т.к. начальные условия одинаковы.
Пусть 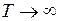 . Заметим, что
. Заметим, что 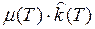 - величина положительная, она только усиливает знак неравенства. Нам могло бы помешать только слагаемое
- величина положительная, она только усиливает знак неравенства. Нам могло бы помешать только слагаемое 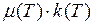 , но условие трансверсальности (6) дает
, но условие трансверсальности (6) дает 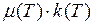
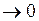 при
при 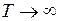 .Утверждение доказано.
.Утверждение доказано.
Докажем теперь, что на оптимальной траектории условие трансверсальности должно выполняться. Имеем 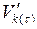 =
= 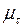 . Легко проверить, что максимальное значение функционала
. Легко проверить, что максимальное значение функционала 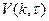 – вогнутая функция от
– вогнутая функция от 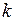 . Переменную
. Переменную 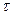 в дальнейшем опускаем. Для произвольного положительного
в дальнейшем опускаем. Для произвольного положительного 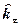 , имеем:
, имеем:
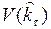
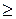 0;
0;
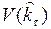
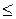
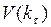 +
+ 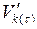 (
(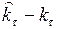 ). Следовательно
). Следовательно
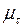 (
(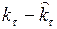 )
) 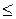
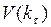 =
= 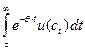 . Поэтому
. Поэтому
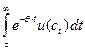
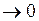 при
при 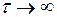 , если интеграл сходится.
, если интеграл сходится.
Положим 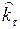 = ½
= ½ 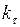 . Тогда получим
. Тогда получим
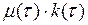
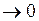 при
при 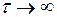 ,
,
что и требовалось
|
|
|
Заметим, что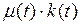 можно интерпретировать как стоимость капитала в момент t. С экономической точки зрения не имеет смысла на бесконечности иметь капитал положительной стоимости: это означало бы, что мы не воспользовались возможностью его "проесть" и увеличить значение функционала.
можно интерпретировать как стоимость капитала в момент t. С экономической точки зрения не имеет смысла на бесконечности иметь капитал положительной стоимости: это означало бы, что мы не воспользовались возможностью его "проесть" и увеличить значение функционала.
Запишем условия оптимальности в более удобной форме.
Из (5) и (6) получаем:
(5а) 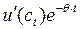 =
= 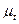
(5в) 
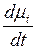 = –
= – 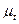
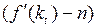
Подставим (5а) в (5в).
(7) 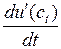 =
= 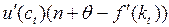
Это уравнение Эйлера – Лагранжа для нашей задачи.
Перепишем условие (6):
(8) 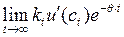 = 0
= 0
Уравнение (8) могло быть получено из основного уравнения вариационного исчисления.
Запишем интеграл (1) в виде 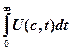 , где U =
, где U = 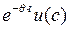 . Подставим
. Подставим 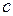 ,
,
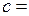
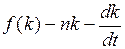 ,
,
в формулу для функционала, и не будем обращать внимание на то, что у нас задача с бесконечным временем. Как известно, уравнение Эйлера – Лагранжа для такой задачи вариационного исчисления имеет вид:
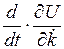 =
= 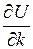
Отсюда легко получить (7).
Зачем же тогда применять принцип максимума?
1) Оценки 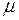 хорошо интерпретируются и придают больше содержательности условиям первого порядка.
хорошо интерпретируются и придают больше содержательности условиям первого порядка.
2) Условие трансверсальности естественно формулировать в терминах оценок.
 2014-02-13
2014-02-13 1161
1161






