Представим уравнение (11.2) в другом виде. Подставим в него выражение для 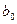 :
:
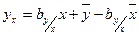 ,
,
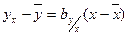 . (11.3)
. (11.3)
Из формулы (11.3) видно, что коэффициент регрессии 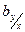 показывает на сколько единиц изменится переменная
показывает на сколько единиц изменится переменная  при увеличении переменной
при увеличении переменной  на 1 единицу. Это не всегда является удобным, так как
на 1 единицу. Это не всегда является удобным, так как 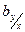 зависит от единиц измерения.
зависит от единиц измерения.
Умножим 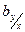 на
на 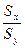 , тогда (11.3) имеет вид
, тогда (11.3) имеет вид
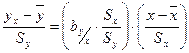 .
.
Обозначим через 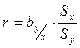 . (11.4)
. (11.4)
Определение. Величина 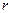 является показателем тесноты связи и называется выборочным коэффициентом корреляции, равный
является показателем тесноты связи и называется выборочным коэффициентом корреляции, равный
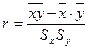 . (11.5)
. (11.5)
Выборочный коэффициент корреляции 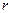 показывает на сколько величин
показывает на сколько величин 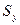 изменится в среднем
изменится в среднем  , когда
, когда  увеличится на одно
увеличится на одно 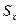 .
.
Т.к. формула для 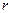 (11.5) симметрична относительно двух переменных, то можно записать:
(11.5) симметрична относительно двух переменных, то можно записать:
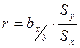 . (11.6)
. (11.6)
Найдя произведение обеих частей равенств (11.4) и (11.6), получим
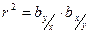 или
или
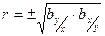 ,
,
т.е. коэффициент корреляции 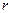 есть средняя геометрическая коэффициентов регрессии, имеющая их знак.
есть средняя геометрическая коэффициентов регрессии, имеющая их знак.
Т.о. теоретическая линия регрессии  по
по  имеет вид:
имеет вид:
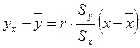 .
.
Аналогично определяется теоретическая линия регрессии  по
по  :
:
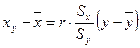 .
.
Замечание. Обе теоретические линии регрессии проходят через точку 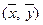 .
.
|
|
|
Найдем уравнения теоретических линий регрессии для нашей таблицы распределения.
Вычислим коэффициент корреляции 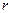 . Для этого проведем расчеты
. Для этого проведем расчеты 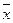 ,
, 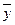 ,
, 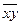 ,
, 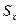 ,
, 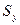 .
.



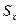 =
=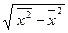 ,
, 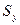 =
=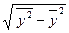 .
.




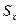 =
=
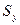 =
=
Т.о. 
Теоретическая линия регрессии  на
на  :
:
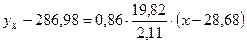 или
или
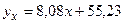 .
.
Теоретическая линия регрессии  на
на  :
:
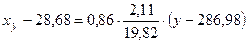 или
или
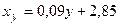 .
.
Свойства выборочного коэффициента корреляции r
1) 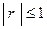 - абсолютная величина не превосходит единицы.
- абсолютная величина не превосходит единицы.
2) При 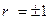 корреляционная связь представляет собой линейную функциональную зависимость. При этом линии регрессии
корреляционная связь представляет собой линейную функциональную зависимость. При этом линии регрессии  по
по  и
и  по
по  совпадают.
совпадают.
3) При 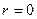 линейная корреляционная связь отсутствует. Линии регрессии параллельны осям координат.
линейная корреляционная связь отсутствует. Линии регрессии параллельны осям координат.
4) Если 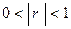 , то с.в.
, то с.в. и
и  связаны корреляционной зависимостью. Чем ближе
связаны корреляционной зависимостью. Чем ближе 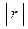 к единице, тем сильнее эта зависимость.
к единице, тем сильнее эта зависимость.
Проверка значимости выборочного коэффициента корреляции 
Пусть из двумерной генеральной совокупности 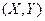 извлечена выборка объема n и по ней найден выборочный коэффициент корреляции
извлечена выборка объема n и по ней найден выборочный коэффициент корреляции 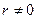 . Так как выборка случайная, то нельзя заключить, что коэффициент корреляции генеральной совокупности
. Так как выборка случайная, то нельзя заключить, что коэффициент корреляции генеральной совокупности 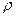 также отличен от нуля. Поэтому при заданном уровне значимости
также отличен от нуля. Поэтому при заданном уровне значимости 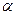 проверяем гипотезу
проверяем гипотезу 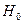 об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е.
об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е. 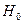 :
: 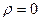 .
.
Если нулевая гипотеза отвергается, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля, а Х и Y связаны линейной зависимостью.
В качестве критерия проверки нулевой гипотезы принимают случайную величину
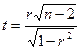 .
.
Величина 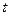 имеет распределение Стьюдента с
имеет распределение Стьюдента с 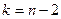 степенями свободы.
степенями свободы.
Правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости 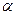 проверить нулевую гипотезу
проверить нулевую гипотезу 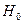 :
: 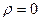 , надо вычислить наблюдаемое значение критерия
, надо вычислить наблюдаемое значение критерия 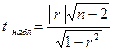 и по таблице критических точек распределения Стьюдента найти критическую точку
и по таблице критических точек распределения Стьюдента найти критическую точку 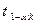 .
.
|
|
|
Если 
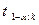 - нет оснований отвергнуть нулевую гипотезу.
- нет оснований отвергнуть нулевую гипотезу.
Если 
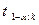 - нулевую гипотезу отвергают.
- нулевую гипотезу отвергают.
 2014-02-09
2014-02-09 283
283






