2014-02-09
2857В лекции 4 мы видели, что поиск элемента в упорядоченном массиве (бинарный поиск) выполняется значительно быстрее, чем в неупорядоченном. Если поиск нужно вести многократно, то становится выгодным один раз упорядочить массив и затем пользоваться бинарным поиском.
Упорядочение последовательности называется сортировкой.
Сортировка — это, наверное, самая детально исследованная задача в информатике. Нет ни одной книги по алгоритмам, в которой отсутствуют алгоритмы сортировки. Это обусловлено рядом причин. Во-первых, сортировка часто используется на практике — нет ни одной системы программирования, в которой не было бы реализовано несколько алгоритмов сортировки. Д Кнут пишет, что «во многих вычислительный системах на нее уходит больше половины машинного времени» [3]. Во-вторых, алгоритмы сортировки являются интересными примерами программирования. В-третьих, сортировка является одной из немногих задач с точными теоретическими ограничениями производительности.
Формально задача сортировки формулируется следующим образом. Пусть имеется последовательность из N элементов R1, R2, …, RN, называемых записями. Каждая запись Ri имеет ключ Ki. Требуется найти такую перестановку p(1), p(2), …, p(N) записей, в которой ключи расположены в порядке неубывания:
|
|
|
Kp(1) ≤ Kp(2) ≤ … ≤ Kp(N) (5.1)
Иногда требуется расположить записи в порядке невозрастания.
Сортировка называется устойчивой, если записи с одинаковыми ключами сохраняют свой исходный порядок.
Методы сортировки обычно делятся на два класса: внутренние и вешние. Внутренняя сортировка предполагает, что все записи (или, по крайней мере, все ключи) последовательности помещаются в оперативной памяти. Внешняя сортировка имеет дело с внешними файлами, которые полностью в оперативную память не помещаются. Для внешней сортировки наиболее актуальной является проблема минимизации количества обменов с внешним устройством, поскольку эта операция занимает значительно больше времени, чем непосредственно сортировка.
Алгоритмы внутренней сортировки обычно имеют эффективность порядка O(NAlogN). C другой стороны, ряд простых алгоритмов работает со скоростью O(N2). Если же известно, что ключи являются случайными величинами с некоторым непрерывным распределением, то сортировка может быть выполнена в среднем за O(N) шагов.
Внутренняя сортировка
Во всех методах внутренней сортировки будем рассматривать сортировку последовательности ключей, на множестве которых введено отношение порядка «<». Отношение порядка на множестве ключей вводится таким образом, чтобы для любых ключей a, b, c выполнялись следующие условия:
|
|
|
справедливо одно и только одно из соотношений a < b, a = b, a > b;
если a < b и b < с, то a < c;
Эти два свойства определяют математическое понятие линейного порядка, которое называется также совершенным порядком
Для внутренних сортировок обычно вычисляют количество сравнений ключей и количество перестановок (или присваиваний) записей. Будем считать, что операция перестановки двух записей выполняется процедурой swap(x,y):
swap(x,y)
{ t = x; x = y; y = t; }
Если ключи представляют собой элементарный встроенный тип данных (например, целые числа), а записи не являются элементарным типом, то операция перестановки записей может занимать значительно больше времени, чем операция сравнения. Если размер записи слишком велик, то для уменьшения времени можно использовать различные приемы. Одним из них является преобразование массива в список. Тогда вместо перестановок объемных записей выполняется перестановка указателей. Указатели обычно являются элементарным встроенным типом, и присваивание указателей выполняется очень быстро.
Другой способ избавиться от перестановок непосредственно записей состоит в том, что ключи выносятся в отдельный массив и к каждому ключу присоединяется индекс (номер) его записи в исходном массиве. Обычно индекс является целым числом в машинном диапазоне целых чисел, поэтому он занимает не более 4-8 байт. Вместо исходного массива сортируется такой массив ссылок. Перестановки в массиве индексов выполняются очень быстро. Вместо индексов можно использовать и указатели.
Учитывая сказанное, будем считать, что во всех алгоритмах сортируется последовательность ключей, размещенных в массиве A. В некоторых случаях для сравнения будет рассмотрен вариант алгоритма для сортировки списка.
Сортировка выбором
Сортировка выбором представляет собой применение метода грубой силы для решения задачи сортировки. Идея сортировки выбором основана на поиске минимума (максимума). На первом шаге выбирается минимальный элемент из последовательности A[1], …, A[N] и меняется с A[1], на втором шаге минимальный элемент выбирается из последовательности A[3], …, A[N] и меняется с A[3], и так далее. На i-м шаге сортировки среди элементов массива A[i], …, A[N] выбрать минимальный и обменять его с элементом A[i]. На i-м шаге будет отсортирована последовательность A[1], …, A[i].
Алгоритм 5.1. Сортировка выбором
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
for i = 1 to n-1
{ min = i;
for j = i + 1 to n
{ if(A[j]<A[min] min = j; }
swap(A[i],A[min]);
}
Основной операцией является операция сравнения ключей. Общее количество cравнений равно
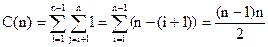(5.2)
Алгоритм имеет эффективность (по операции сравнения) t(n) = O(n2). Отметим, что по операции перестановки эффективность алгоритма линейна, t(n) = O(n). Нетрудно посчитать, что алгоритм выполняет ровно n-1 обмен. Заметим также, что и в худшем, и в среднем, и в лучшем случае эффективность по сравнениям совершенно одинакова.
Сортировка обменом
Еще один алгоритм грубой силы — сортировка «пузырьком». Он основан на сравнении рядом стоящих элементов. Если они расположены не в нужном порядке, они меняются местами.
Алгоритм 5.2. Сортировка простым обменом (пузырек)
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
for i = 1 to n-1
{ for j = 1 to n-1-i
{ if(A[j+1]<A[j] swap(A[j],A[j+1]); }
}
Как показано во всех источниках, и в худшем, и в среднем случаях количество сравнений пропорционально n2. Эффективность с точки зрения обменов зависит от входных данных, но в худшем случае алгоритм тоже принадлежит классу O(n2).
Небольшое усовершенствование позволит несколько ускорить алгоритм. Для этого нужно использовать булевскую переменную, которая будет сигнализировать о наличии перестановок во внутреннем цикле. Если ни одной перестановки не произошло, то массив отсортирован, и можно завершать работу.
|
|
|
Алгоритм 5.3. Сортировка простым обменом (пузырек)
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
i = N;
swapped = true;
while(swapped)
{ i = i – 1;
swapped = false;
for j = 1 to i
{ if(A[j+1]<A[j]
{ swap(A[j],A[j+1]);
swapped = true;
}
}
}
Хотя мы избавились от проверки индексной переменной во внешнем цикле, и работа данного алгоритма прекращается при отсутствии обменов во внутреннем цикле, тем не менее, и в худшем, и в среднем случае он по-прежнему относится к классу O(n2). А вот в лучшем случае такой алгоритм выполняет только n-1 сравнение. Таким образом, сортировка «пузырьком» лучше работает с почти отсортированными массивами.
Еще одним усовершенствованием является изменение направления прохода во внутреннем цикле: сначала слева направо (или сверху вниз), потом справа налево (или снизу вверх). Эта модификация удостоилась собственного названия «шейкер-сортировка» [3],[32]. Однако и этот алгоритм тоже относится к классу квадратичных.
Сортировка вставками
Сортировка вставками представляет собой применение метода уменьшения размера к задаче сортировки. Алгоритм выполняет вставку очередного элемента в уже упорядоченную последовательность. Считая, что элементы A[1], …, A[i-1] уже отсортированы, вставляем в подходящее место элемент A[i].
Алгоритм 5.4. Сортировка простой вставкой
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
for i = 2 to n
{ v = A[i]; // выбрали элемент
j = i - 1;
while(j > 0)&(A[j]>v) // «сдвиг» вправо
{ A[j+1] = A[j]; // всех A[j]>v
j = j – 1;
}
A[j+1] = v; // вставка на место
}
Алгоритм выбирает очередной элемент массива и помещает его в переменную v. Далее в цикле вправо перемещаются все элементы массива, большие v, освобождая место для вставки v.
Количество сравнений, очевидно, зависит не только от N, но и от их расположения. В худшем случае элементы массива расположены в обратном порядке, и алгоритм выполняет максимум сравнений и перестановок. В этом случае и количество сравнений, и количество перестановок равно n(n-1)/2.
|
|
|
В лучшем случае, когда массив уже отсортирован, количество сравнений равно n, а перестановок не выполняется ни одной. Таким образом, алгоритм имеет наилучшую производительность на почти отсортированных массивах.
В среднем же сортировка простыми вставками выполняет примерно вдвое меньше сравнений (и присваиваний), чем в худшем случае: Cср ≈ n2/4.
Алгоритм 5.4 можно улучшить. Небольшое улучшение состоит в установке барьера в A[0] — это избавит нас от проверки j>0 во внутреннем цикле. Более серьезное улучшение состоит в применении бинарного поиска. Во внутреннем цикле алгоритм выполняет последовательный поиск места вставки. Однако поиск выполняется в отсортированном массиве, поэтому поиск места вставки вполне можно выполнить посредством более быстрого алгоритма: бинарного или интерполяционного поиска. Алгоритм с бинарным поиском места вставки получил собственное название «сортировка бинарными вставками».
Алгоритм 5.5. Сортировка бинарными вставками
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
for i = 2 to n
{ v = A[i]; // выбрали элемент
L = 1; R = i – 1; // граница сортированной части
while(L ≤ R)
{ m = (L+R)/2; // вычисление середины
if(v < A[m])
R = m - 1; // смотрим левую половину
else
L = m + 1; // смотрим правую половину
}
j = i - 1;
while(j > L)
{ A[j+1] = A[j]; // перемещение
j = j – 1; // элементов
}
A[L] = v; // вставка на место
}
Бинарный поиск сразу уменьшает количество сравнений до O(nlogn). Однако количество перестановок элементов остается прежним, поэтому даже в этом случае алгоритм относится к классу квадратичных.
Алгоритм сортировки простой вставкой прекрасно подходит для сортировки списков, поскольку в этом случае не нужно сдвигать элементы вправо — выполняются только сравнения. Итак, пусть у нас есть двусвязный линейный список L с заголовком H = (0,nh,ph).
Алгоритм 5.6. Сортировка простой вставкой (список)
// Входные данные: неупорядоченный список L из n элементов
// Выходные данные: упорядоченный список L
p = nh; // первый элемент
insert_first(-∞); // прицепляем «барьер»
p = p->nx; // второй элемент
while (p!= 0) // до конца списка
{ q = p->px; // хвост сортированного списка
while (p->x < q->x) // продвигаемся к месту вставки
{ q = q->px; }
if(q!= p->px) // надо ли переставлять?
{ t = p;
exclude(t); // отцепили со своего места
include(t,q); // прицепили в нужное место
}
p = p->nx; // следующий вставляемый элемент
}
exclude_first(); // отцепили барьер
Сначала указатель p устанавливается на первый элемент списка. Затем в начало списка вставляется барьер — элемент с ключом заведомо меньшим, чем все элементы списка. Указатель p продвигается на следующий элемент и с этого момента всегда показывает на вставляемый элемент (в алгоритме 5.4 это v = A[i]). Далее следует основной цикл продвижения по списку. В цикле указатель q устанавливается на предшественника p. Далее осуществляется поиск элемента, после которого нужно вставить элемент: указатель q «бежит» влево, пока выполняется неравенство
(p->x < q->x). Как только неравенство нарушается, происходит выход из цикла. В этот момент q показывает на элемент списка, после которого нужно вставлять проверяемый элемент. Цикл обязательно завершится, поскольку установлен барьер с заведомо меньшим ключом. В этом случае q будет показывать на элемент-барьер, и проверяемый элемент будет вставлен после барьера, то есть на первое место в списке.
Возможет другой крайний случай: ключ вставляемого элемента оказался больше последнего элемента отсортированной части списка (вложенный цикл не выполнится ни разу). Тогда проверяемый элемент никуда переставлять нет необходимости, а нужно просто перейти к следующему элементу списка. Именно для этого выполняется проверка (q!= p->px).
Очевидно, что эффективность этого алгоритма по сравнениям подобно алгоритму 5.4 является квадратичной. А вот по операциям перестановок алгоритм со списком значительно эффективнее, поскольку элементы списка никуда не перемещаются физически, каждая операция вставки занимает фиксированное и очень малое время. Максимальное количество таких вставок будет n — в самом худшем случае. Поэтому по вставкам алгоритм относится к линейным с эффективностью O(n).
Сортировка Шелла
Идея алгоритма состоит в обмене элементов, расположенных не только рядом, как в алгоритме простых вставок (алгоритм 5.4), но и далеко друг от друга, что значительно сокращает общее число операций перемещения элементов. Для примера возьмем последовательность Д.Кнута [3] из 16 элементов:
Сначала просматриваются пары с шагом 8. Это пары элементов 1-9, 2-10, 3-11, 4-12, 5-13, 6-14, 7-15, 8-16. Если значения элементов в паре не упорядочены по возрастанию, то элементы меняются местами. Назовем этот этап 8-сортировкой. После этого этапа последовательность принимает вид:
Следующий этап — 4-сортировка, на котором элементы в файле делятся на четверки: 1-5-9-13, 2-6-10-14, 3-7-11-15, 4-8-12-16. Выполняется сортировка в каждой четверке. Сортировка может выполняться методом простых вставок. После этого этапа последовательность примет вид:
Следующий этап — 2-сортировка, когда элементы в файле делятся на 2 группы по 8: 1-3-5-7-9-11-13-15 и 2-4-6-8-10-12-14-16. Выполняется сортировка в каждой восьмерке. После этого последовательность примет вид:
Наконец вся последовательность упорядочивается методом простых вставок. Поскольку дальние элементы уже переместились на свое место или находятся вблизи от него, этот этап будет значительно менее трудоемким, чем при сортировке вставками без предварительных «дальних» обменов. Последовательность примет свой окончательный вид:
Как пишет Д.Кнут [3], последовательность 8, 4, 2, 1-сортировок не является обязательной. Подойдет любая последовательноcть ht, ht-1, …, h2, h1 с условием, что h1 = 1. При t = 1 алгоритм сводится к алгоритму 5.4. Дадим алгоритм сортировки Шелла как он описан у Д.Кнута [3].
Алгоритм 5.7. Сортировка Шелла
// Входные данные: массив А из n элементов а1,а2,...,аN;
последовательность ht, ht-1, …, h2, h1ж
// Выходные данные: отсортированный массив A
[Цикл по s]. Выполнить шаг 2 при s = t, t-1, …, 1, после чего закончить
[Цикл по j]. h = h[s]; выполнить шаги 3,4,5,6 при h < j ≤ N.
[Установка i, v]. i = j – h; v = A[j];
[Сравнение ]. Если v > A[i], то перейти к шагу 6;
[Перемещение Ai, уменьшение i]. A[i+h] = A[i]; i = i-h; если i > 0, перейти к 4;
[Перемещение v]. A[i+h] = v;
Сортировка Шелла была глубоко проанализирована. Д.Кнут сообщает, что уже при двух проходах для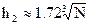 
и h1 = 1 эффективность сортировки повышается с O(n2) до O(n1.667). Много исследований было посвящено выбору наилучшей последовательности чисел hs. Была доказана теорема:
Теорема 5.1. Если hs = 2s+1- 1 при 0 ≤ s < t = [log2N], то время сортировки по алгоритму 5.7 есть O(N3/2).
Это уже значительно лучше, чем O(n2). Хотя сортировка Шелла была придумана в 1959 году, вопрос о лучшей последовательности смещений h остается открытым. В 1986 году (почти через 30 лет!) Р.Седжвик предложил следующую эмпирическую формулу для вычисления hs:
hs = 9A2s - 9A2s/2 + 1, если s четно;
hs = 8A2s - 6A2(s+1)/2 + 1, если s нечетно; (5.3)
Эта формула позволяет достичь производительности O(N7/6). В практических целях Д.Кнут предлагает для малых N использовать простую формулу:
h1 = 1, hs+1 = 3hs +1; остановиться на ht при 3ht+1 > N. (5.4)
Для больших N он рекомендует пользоваться формулой Р.Седжвика (5.3).
Быстрая сортировка
Этот алгоритм был придуман Хоаром в 1962 году. Быстрая сортировка называется также сортировкой с разделением. Эта сортировки является ярким представителем применения метода декомпозиции («разделяй и властвуй»).Алгоритмы, основанные на методе декомпозиции, работают по следующему плану:
Задача разбивается на несколько меньших задач, желательно одинакового объема.
Решаются задачи меньшего объема (обычно рекурсивно).
При необходимости решение исходной задачи находится путем комбинации решений меньших задач.
Идея быстрой сортировки состоит в следующем:
Выбирает элемент Х последовательности, называемый осевым (опорным);
Все элементы последовательности ai < X, перемещаются влево от Х, все элементы ai > X перемещаются вправо от Х.
Эти действия повторяются с левой и правой частью последовательности.
Шаг 2 называется процедурой разделения. Алгоритм быстрой сортировки является рекурсивным и выглядит на удивление простым.
Алгоритм 5.8. Быстрая сортировка (Хоар)
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
QuickSort(A,L,R)
{ if (L < R)
{ s = Partition(A,L,R); // s – позиция разбиения
QuickSort(A,L,s-1); // левая половина
QuickSort(A,s+1,R); // правая половина
}
}
QuickSort(A,1,N); // первый вызов
Весь фокус, конечно, кроется в процедуре разделения — именно она перемещает меньшие элементы налево, а большие — направо. Поэтому эффективность быстрой сортировки практически целиком зависит от этой процедуры. Наиболее просто и понятно эта процедура описана в [32].
Алгоритм 5.9. Процедура разделения
// Входные данные: часть массива А аL,аL+1,...,аR;
// Выходные данные: позиция осевого элемента s;
Partition(A,L,R)
i = L; j = R;
s = (L+R)/2; // позиция осевого элемента
x = A[s]; // осевой элемент
do
{ while(A[i] < x) i = i + 1;
while(x < A[j]) j = j - 1;
if(i ≤ j)
{ swap(A[i],A[j]);
i = i + 1;
j = j – 1;
}
} while(i < j);
return s;
В этой процедуре в качестве разделяющего элемента выбирается элемент посередине массива. Эффективность, однако, зависит не от места элемента, а от его значения. С таким же успехом мы могли бы выбрать первый элемент, или последний, или случайный. Если вдруг случайно окажется, что мы выбрали минимум или максимум, то все элементы окажутся по одну сторону этого элемента. Такое разбиение — это один из наихудших вариантов. Другие наихудшие случаи — массив одинаковых элементов и отсортированный массив. Во всех этих вариантах производительность алгоритма пропорциональна квадратичной O(n2).
Поэтому выбор «хорошего» осевого элемента — главная проблема алгоритма быстрой сортировки. Если все время выбирается медиана последовательности, то это является наилучшим вариантом разделения. В этом случае, как показано в [32], общее число сравнений равно nlog(n), а общее число обменов — (n/6)log(n). Но это — оптимальный вариант. В среднем же эффективность хуже оптимальной, но всего в 2ln(2) раз.
Поскольку в среднем на случайных массивах быстрая сортировка ведет себя очень хорошо, для повышения эффективности в наихудшем случае обычно выбирают разделяющий элемент как среднее из трех случайных элементов массива. Этот подход называется методом медианы трех элементов.
Существует и нерекурсивный алгоритм сортировки разделением, описанный в [3] и [32], однако он достаточно сложен, и фактически моделирует рекурсию, так как в явном виде используется стек.
Сортировка слиянием
Еще один алгоритм, построенный по методу декомпозиции — это сортировки слиянием. Этот метод является фактически первым методом сортировки, описанным еще Джоном фон Нейманом в 1945 году.
В этом алгоритме, в отличие от предыдущего (быстрая сортировка), разделение массива делается по индексу, а не по значению. Элементы не перемещаются. Напротив, разделение выполняется до размера в 1 элемент, после чего начинается слияние.
Алгоритм 5.10. Сортировка слиянием
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
MergeSort(A,L,R)
{ if (L < R)
{ m = (L+R)/2; // m – середина массива
MergeSort(A,L,m); // левая половина
MergeSort(A,m+1,R); // правая половина
Merge(A, L,m,m+1,R); // слияние
}
MergeSort(A,1,N); // первый вызов
В этом алгоритме всю работу проделывает процедура Merge(), которая и выполняет слияние. Процедура использует вспомогательный массив размером равный сумме сливаемых массивов.
У Д.Кнута в [3] этот алгоритм называется двухпутевым слиянием. Входом являются два отсортированных массива в общем случае разной длины. Алгоритм слияния широко применяется во внешних сортировках файлов (см. ниже).
Алгоритм 5.11. Двухпутевое слияние (Merge)
// Входные данные: два упорядоченных массива А = а0,а2,...,аN-1, B = b0,b2,...,bM-1;
// Выходные данные: отсортированный массив D размером N+M;
[Начальные установки]. i = j = k = 0;
[Выбрать меньший элемент]. Если A[i] < B[j], то выполнить 3; иначе выполнить 5;
[Поместить ai]. D[k] = A[i]; k = k +1; i = i +1; если i < N< то перейти к 2;
[Поместить хвост B]. Установить (D[k],…,D[N+M-1]) = (B[j],…,B[M-1]) и завершить;
[Поместить bj]. D[k] = B[j]; k = k +1; j = j +1; если i < M то перейти к 2;
[Поместить хвост A]. Установить (D[k],…,D[N+M-1]) = (A[i],…,A[N-1]) и завершить;
Псевдокод алгоритма вы найдете в [4] и [7].
Эффективность алгоритма линейна и пропорциональна O(N+M). В алгоритме MergeSort() слияние выполняется для массивов, чей размер отличается максимум на 1. Кроме того, слияние не начинается до тех пор, пока длина сливаемых массивов не станет равной 1. Массив длиной 1 по определению является отсортированным, поэтому слияние прекрасно работает.
Эффективность в целом алгоритма сортировки слиянием в худшем случае не превышает O(nlogn). Это один из двух алгоритмов с гарантированной производительностью.
Сортировки за линейное время
В некоторых специальных случаях, когда ключи являются целыми числами, возможно выполнить сортировку за линейное время O(n). Аналогично тому, как при интерполяционном поиске используется информация о равномерном распределении ключей, возможности сортировки за линейное время появляются при некоторой дополнительной информации. Кроме того, выше речь шла о сортировках, основной операцией которых является операция сравнения. Для сортировок сравнением была доказана теорема:
Теорема 5.2. В наихудшем случае в ходе выполнения любого алгоритма сортировкой сравнением выполняется Ω(NlogN) сравнений.
Это означает, что сортировка сравнением не может быть выполнена менее, чем за O(NlogN) сравнений. Поэтому, если есть возможности выполнить сортировку быстрее, речь идет не об операциях сравнения.
Сортировка подсчетом
Как сказано в [8], алгоритм сортировки подсчетом использует метод пространственно-временного компромисса. За счет использования некоторого количества дополнительной памяти удается существенно повысить производительность алгоритма. Например, если элементы последовательности представляют собой не повторяющиеся целые числа от 1 до N, и у нас есть N «лишних» слов памяти, то «сортировка» превращается в присваивание:
for i = 1 to N
B[A[i]] = A[i];
Сам ключ является индексом в новом массиве. Для таких чисел можно отсортировать массив и без использования «лишней» памяти:
for i = 1 to N
while(A[i]!= i)
swap(A[i],A[A[i]]);
Если элементы последовательности — это числа в диапазоне от 0 до k (или приводятся к этому диапазону), причем k существенно меньше N, то используя дополнительный массив из k элементов можно также выполнить сортировку за линейное время.
for i = 0 to k
d[i] = 0;
for i = 1 to N
d[A[i]]= d[A[i]] + 1;
j = 0;
for i = 1 to N
{ A[i] = j;
d[j] = d[j] – 1;
if (d[j] = 0) j = j + 1;
}
Первый цикл обнуляет массив счетчиков d, во втором цикле подсчитывается количество появлений каждого числа в исходном массиве. Третий цикл записывает числа в тот же массив А, используя счетчики в d.
Сортировка подсчетом выполняется для записей с ключами, которые являются целыми числами в диапазоне от 0 до k (или приводятся к такому диапазону), причем k существенно меньше N. Однако запись — это не только ключ, поэтому в данном случае без использования второго массива обойтись не удастся: записи из исходного массива требуется помещать в массив-результат. Однако время сортировки по-прежнему линейно. Основная идея состоит в том, чтобы определить место в новом массиве, в которое требуется помещать элементы исходного массива. Это можно сделать, если вычислить для каждого элемента ai количество элементов, которые меньше него.
Алгоритм 5.12. Сортировка подсчетом
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив S
for i = 0 to k // обнуление счетчиков
d[i] = 0;
for i = 1 to N // подсчет
d[A[i]]= d[A[i]] + 1;
// в d[i] - количество элементов с ключом i
for i = 1 to k // обнуление счетчиков
d[i] = d[i] + d[i-1];
// в d[i] - количество элементов, не превышающих i
for j = N to 1 // в обратном порядке
{ S[d[A[j]]]] = A[j];
d[A[j]] = d[A[j]] – 1;
}
Обратите внимание, что не требуется дополнительного индекса для массива счетчиков! Таким образом, массив A просматривался дважды, поэтому количество операций пропорционально 2N. Кроме того, выполняется обработка массива d, содержащего k элементов. Следовательно, эффективность алгоритма относится к классу линейных O(N).
Сортировкам подсчетом обладает важнейшим свойством устойчивости: в отсортированной последовательности элементы с равными ключами сохраняют первоначальный порядок. Это свойство сортировки подсчетом используется в поразрядной сортировке.
Поразрядная сортировка
Сортировка подсчетом может использоваться при реализации поразрядной сортировки, которую иногда называют «цифровой» сортировкой. Идея поразрядной сортировки состоит в том, что ключ представляет собой последовательность k цифр. Каждая цифра принимает значения от 0 до b-1, где b — основание системы счисления. Алгоритм поразрядной сортировки очень прост [3].
Алгоритм 5.13. Поразрядная сортировка
// Входные данные: массив А из n элементов а1,а2,...,аN;
// Выходные данные: отсортированный массив A
for i = 0 to k
Сортировка подсчетом А по i-й цифре
Здесь i представляет собой номер цифры в числе. Вообще-то вместо сортировки подсчетом можно использовать любую сортировку, обладающую свойством устойчивости. Почему это так важно, покажем поразрядную сортировку на примере все той же последовательности Д.Кнута [3].
| 170 | 503 | 061 | |
| 061 | 703 | 087 | |
| 512 | 908 | 154 | |
| 612 | 509 | 170 | |
| 503 | 512 | 275 | |
| 653 | 612 | 426 | |
| 703 | 426 | 503 | |
| 154 | 653 | 509 | |
| 275 | 154 | 512 | |
| 765 | 061 | 612 | |
| 426 | 765 | 653 | |
| 087 | 170 | 677 | |
| 897 | 275 | 703 | |
| 677 | 677 | 765 | |
| 908 | 087 | 897 | |
| 509 | 897 | 908 |
Первый столбец — исходная последовательность, второй — отсортированный по цифре единиц, третий — отсортированный по цифре десятков, последний — отсортированный по цифре сотен. Как мы видим, устойчивость сортировки по отдельной цифре, очень важна — исходные числа сохраняют свои позиции относительно друг друга.
Эффективность поразрядной сортировки, естественно, зависит от эффективности применяемой сортировки по i-й цифре. Если применяется сортировка подсчетом, то количество выполняемых операций пропорционально kN. Если k значительно меньше N, то эффективность поразрядной сортировки — линейная O(N).
В качестве «цифр» можно использовать поля записи. Например, в записи присутствует дата, и требуется отсортировать записи по возрастанию даты. Тогда «старшей цифрой» является поле года, «младшей цифрой» — поле дней, а «средней цифрой» — поле месяцев.
Порядковые статистики
При поиске минимума и максимума (см. алгоритм 4.3) мы упоминали, что эта задача является частным случаем более общей задачи поиска k-го наименьшего элемента. При изучении быстрой сортировки упоминалось, для повышения быстродействия разделяющий элемент m, (элементы меньшие и элементы большие, чем m) должен был являться медианой.
Медианой последовательности из N элементов называется элемент, значение которого меньше или равно одной половины элементов и больше или равно другой половины элементов.
Задача поиска медианы тесно связана с задачей сортировки, так если у нас есть отсортированный массив, то медианой будет являться элемент, который находится в его середине. Задача поиска медианы является частным случаем задачи поиска k-ого наименьшего элемента массива, в случае k=n/2. Алгоритм поиска k-ого наименьшего элемента был предложен Ч.Хоаром и основан на применении процедуры разделения (см. выше алгоритм 5.9).
Пусть L = 1, R = N. В качестве разделяющего выбирается A[k] и выполняется процедура разделения. В результате разделения получаются значения индексов i,j такие, что:
A[h] ≤ A[k] для всех h < i;
A[h] ≥ A[k] для всех h > j;
i > j;
Возможны 3 варианта:
k > i,j — разделяющий элемент слишком велик;
k < i,j — разделяющий элемент слишком мал;
j < k < i — элемент A[k] является искомым.
Процесс разбиения повторяется до случая 3.
Алгоритм 5.14. Поиск k-го по величине элемента
// Входные данные: часть массива А аL,аL+1,...,аR;
// Выходные данные: значение k-го по величине элемента;
L = 1; R = N;
while (L < R)
{ x = A[k];
do
{ while(A[i] < x) i = i + 1;
while(x < A[j]) j = j - 1;
if(i ≤ j)
{ swap(A[i],A[j]);
i = i + 1;
j = j – 1;
}
} while(i < j);
if (j < k) L = i;
if (k < i) R = j;
}
return A[k];
Если предположить, что в среднем при каждом разбиении размер обрабатываемой части массива уменьшается вдвое, то количество сравнений равно
N + N/2 + N/4 + … + 2 + 1 = 2N
Это означает, что алгоритм имеет линейную O(N) эффективность в среднем случае. Правда в наихудшем случае получается все тот же N2, как и для быстрой сортировки. Однако в [4] приводится алгоритм с гарантированной линейной эффективностью O(N) в худшем случае.
Внешняя сортировка
Иногда сортируемая последовательность оказывается настолько велика, что не помещается целиком в память компьютера. Это может быть связано как с количеством элементов последовательности, так и с размером одного элемента. Напомним, что хотя изучаемые нами алгоритмы имеют дело с упорядочиванием ключей, подразумевается, что эти ключи связаны с целыми записями. Во многих случаях длина записи значительно превышает длину ключа. В таких случаях последовательности обычно хранятся на внешних носителях в виде файлов.
Пусть последовательность из N записей записана на внешнем носителе (на магнитном диске и магнитной ленте). Пусть количества памяти хватает только на m записей, причем m значительно меньше N. Основная идея всех внешних сортировок состоит в использовании одного из вариантов слияния. Сначала файл разбивается на ряд серий длиной m, каждая серия сортируется, а затем серии постепенно объединяются в общий файл процедурой слияния (см. алгоритм 5.11). Мы рассмотрим вариант внешней сортировки, описанной в [7] под названием «многофазная сортировка слиянием».
Сначала исходный файл inFile разбивается на 2 файла F1 и F2, в которые записываются сортированные серии. Пусть массив памяти, куда считывается серия, называется M.
Алгоритм 5.15. Разбиение файла на сортированные серии
// Входные данные: исходный файл inFile;
// Выходные данные: два файла F1 и F2 с записанными сортированными сериями длиной m;
CurrentFile = F1;
while(!конец(inFile))
{ read(inFile,M); // читаем m записей в массив M
sort(M); // сортируем серию
if(CurrentFile = F1)
CurrentFile = F2;
else
CurrentFile = F1;
write(CurrentFile,M); // пишем серию
}
После того, как входной файл полностью разбит на отсортированные серии, можно перейти ко второму шагу — слиянию этих серий. Каждый из файлов F1 и F2 содержит некоторую последовательность отсортированных серий, однако, как и в случае сортировки слиянием, мы ничего не можем сказать о порядке следования записей в двух различных сериях.
Процесс слияния аналогичен алгоритму 5.11 (функция Merge()), однако теперь вместо того, чтобы переписывать записи в новый массив, нужно записывать их в новый файл. Поэтому работа начинается с чтения половинок первых серий из файлов из файлов F1 и F2. Читается лишь половина серий, поскольку в памяти может находиться одновременно лишь m записей. Нам нужны записи из обоих файлов, поэтому в память читается m/2 записей из файла F1 и m/2 записей из файла F2. Будем теперь сливать эти половинки отрезков в одну общую серию в файл F3. После того, как одна из половинок закончится, читается вторая половина серии из того же файла. Когда обработка одной из серий будет завершена, конец второй серии будет переписан в файл F3. После того, как слияние первых двух серий из файлов F1 и F2 будет завершено, следующие две серии сливаются в файл F4.
Этот процесс слияния отрезков продолжается с попеременной записью слитых отрезков в файлы F3 и F4. По завершении получится два файла, разбитых на отсортированные серии размером 2m. Затем процесс повторяется, причем серии читаются из файлов F3 и F4, а слитые серии записываются в файлы F1 и F2. Ясно, что в конце концов серии сольются в один отсортированный список в одном из файлов.
Алгоритм 5.16. Слияние сортированных серий
// Входные данные: файлы с сериями F1, F2 длиной m;
// Выходные данные: отсортированный файл CurOut;
Size = m;
Input1 = F1;
Input2 = F2;
CurOut = F3;
while (!done)
{ while (серии не кончились)
{ CurOut = Merge(Input1,Input2);
if (CurOut = F1) CurOut = F2;
else if(CurOut = F2) CurOut = F1;
else if(CurOut = F3) CurOut = F4;
else if(CurOut = F4) CurOut = F3;
}
Size = Size*2;
if(Input1 = F1)
{ Input1 = F3; Input2 = F4; CurOut = F1; }
else
{ Input1 = F1; Input2 = F2; CurOut = F3; }
}
На первом этапе (разделение на серии) получается R = N/m серий. Для слияния такого количества отрезков потребуется [logR]+1 проходов. Если сортировка серии выполняется за O(mlogm) операций сравнения, то количество сравнений при построении всех серий равно O(Rmlogm) = O(Nlogm).
Эффективность слияния по сравнениям равна O(NlogR). Соответственно, общая эффективность равна сумме O(Nlogm + NlogR) = O(NlogN).
Поскольку алгоритм имеет дело с внешними устройствами, то операции чтения-записи занимают много времени. Поэтому нужно оценить их общее количество. На этапе разделения на серии имеем R операций чтения и R операций записи. На этапе слияния имеем 2R операций чтения и R операций записи на один проход. Поскольку проходов logR, то общее количество операций чтения равно R + 2RlogR. Количество операций записи равно R + RlogR.
