Решения нелинейных уравнений

ЛАБОРАТОРНАЯ РАБОТА №1-2.

ИТЕРАЦИОННЫЕ МЕТОДЫ

РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Вариант №5.

Выполнил: Студент группы 24275 Кожевников Е.И.

Проверил: Доцент Горбунов Д.В.

Задание.

Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения 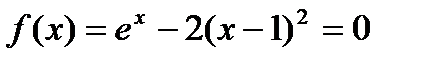на отрезке .

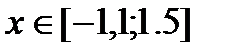Решение:

Графический метод.

Из графика функции 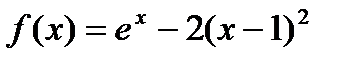на Рис.1 видно, что функция 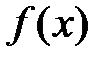пересекает ось 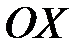в одной точке, являющейся приближенным значением корня нелинейного уравнения. Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение к виду 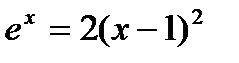и построим два графика 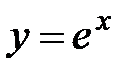и 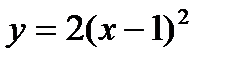, имеющих более простой аналитический вид (Рис.2). Абсцисса точки пересечения графиков является приближенным значением корня.

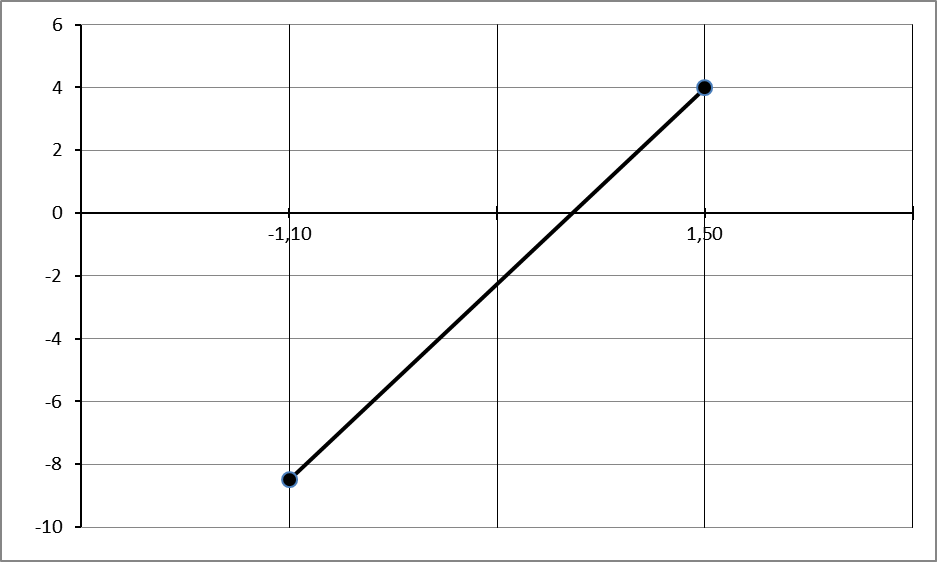
Рис.1 График функции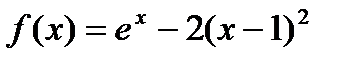

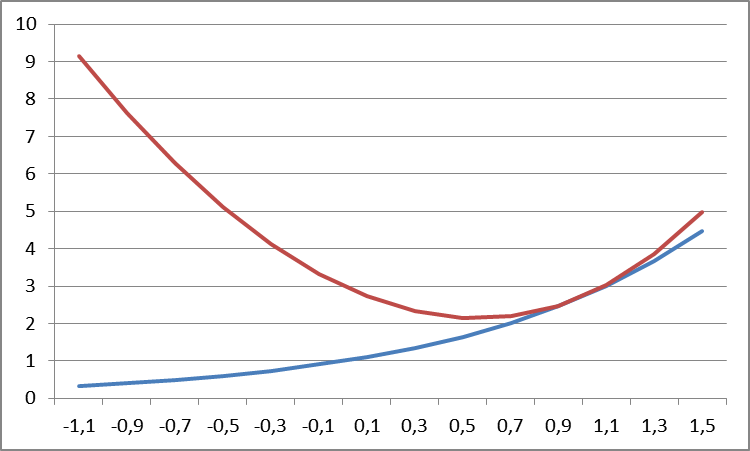
Рис.2 Графики функци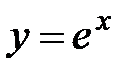й и ,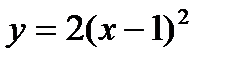

Аналитический метод.

Функция 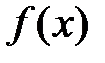непрерывна на отрезке 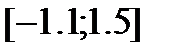, имеет на концах отрезка разные знаки (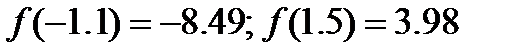), а производная функции 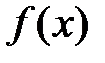не меняет знак на отрезке (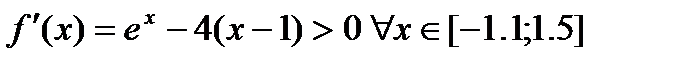). Следовательно, нелинейное уравнение имеет на указанном отрезке единственный корень.

Метод простых итераций.

Построим функцию 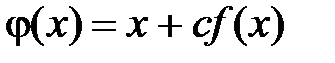. Константа 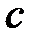выбирается из достаточного условия сходимости:

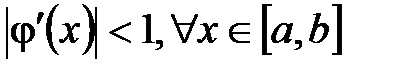
Если производная 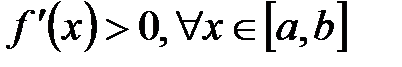, то значение 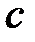выбирается из интервала 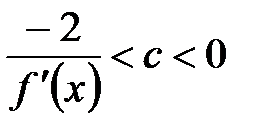, если производная 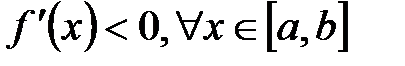, то – из интервала .

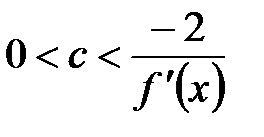Так как для рассматриваемого примера 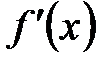всюду положительна на отрезке 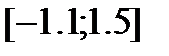, то придавая переменной 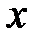различные значения из интервала 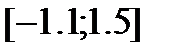и выбирая наименьший интервал 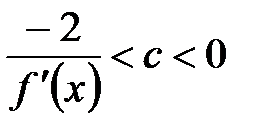, получим .

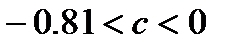Выбираем произвольное значение 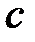из этого интервала.

Пусть 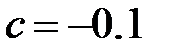. Тогда рабочая формула метода простых итераций будет иметь вид:

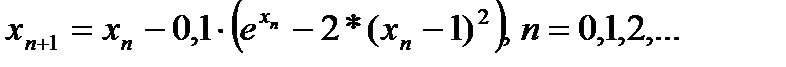
Начнем итерационный процесс, задав начальное приближение х₀ равное минимальному значению х в заданном интервале 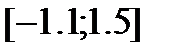, т.е. х₀=-1,1. Итерационный процесс заканчивается при одновременном выполнении двух условий:

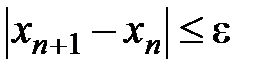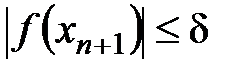и ., где ε=0,001, δ=0,01.

В этом случае значение 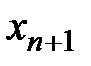является приближенным значением корня нелинейного уравнения на отрезке .

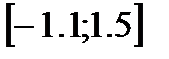Метод Ньютона.

В качестве начального приближения 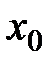здесь выбирается правый или левый конец отрезка, в зависимости от того, в котором выполняется достаточное условие сходимости метода Ньютона вида:

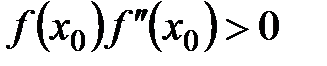
Условие выполняется на обоих концах отрезка, следовательно, в качестве начального приближения разрешено выбрать любой из них. Выбираем наименьший: 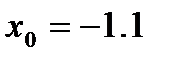. Рабочая формула метода Ньютона 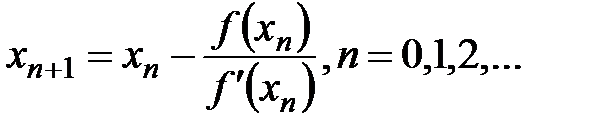для данного уравнения запишется так:

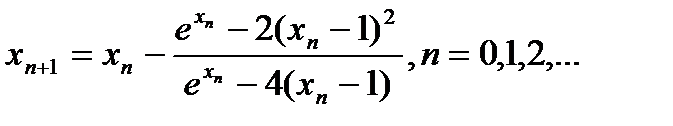
Условия выхода итерационного процесса аналогичны условиям метода простых итераци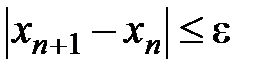й:

и 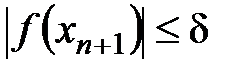., где ε=0,001, δ=0,01.

Модифицированный метод Ньютона.

Начальное приближение 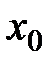выбирается аналогично методу Ньютона, т.е. 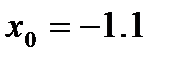. Рабочая формула модифицированного метода Ньютона 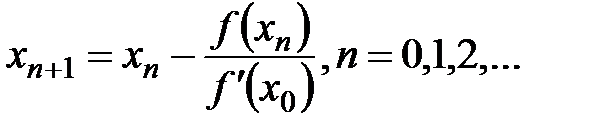для данного примера запишется так:

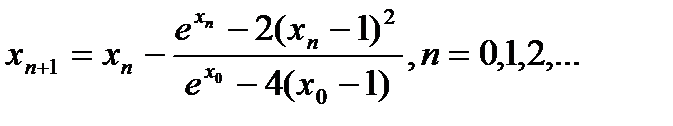
Условия выхода итерационного процесса аналогичны условиям метода простых итераци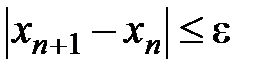й:

и 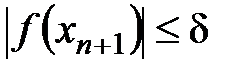., где ε=0,001, δ=0,01.

Блок-схема метода простых итераций, метода Ньютона и модифицированного метода Ньютона приведена на рисунке 3.

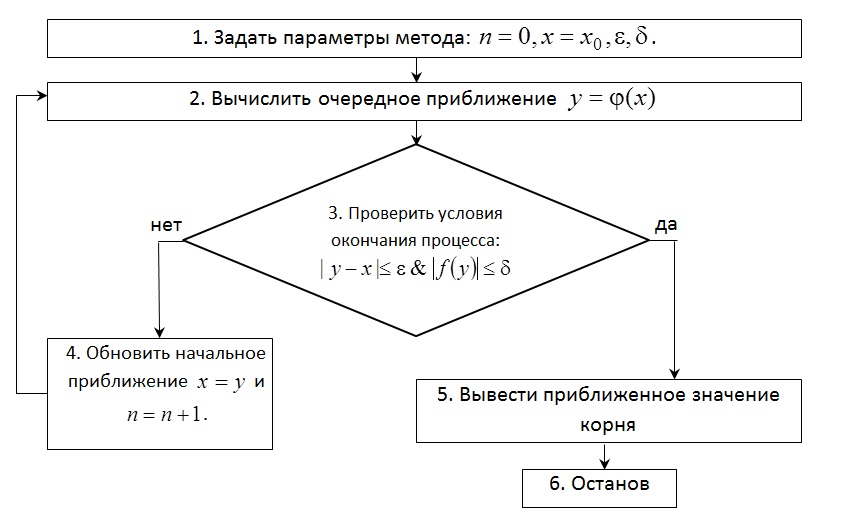
Рис.3 Схема итерационных методов.

Тексты программ:

1) Метод простых итераций:

Program P1_2;

uses Crt;

var n: integer;

x0,x,eps,z,d,y,c:real;

begin

clrscr;

n:=0; x0:=-1.1; c:=-0.1; x:=x0; eps:=0.001; d:=0.01;

writeln (' n xi xi+1 xi+1-xi f(xi+1) ');

repeat

{Метод простых итераций}

y:=x+c*(exp(x)-2*exp(ln(abs(x-1))*2));

writeln (n:3, x:9:5, y:9:5, abs(y-x):9:5, abs(exp(y)-2*(y-1)*(y-1)):9:5);

z:=x;

x:=y;

n:=n+1;

until (abs(x-z)<=eps) and (abs(exp(x)-2*(x-1)*(x-1))<=d);

readln;

end.

2) Метод Ньютона:

Program P1_2_N;

uses Crt;

var n: integer;

x0,x,eps,z,d,y,c:real;

begin

clrscr;

n:=0; x0:=-1.1; c:=-0.1; x:=x0; eps:=0.001; d:=0.01;

writeln (' n xi xi+1 xi+1-xi f(xi+1) ');

repeat

{Метод Ньютона}

y:=x-(exp(x)-2*(x-1)*(x-1))/(exp(x)-4*(x-1));

writeln (n:3, x:9:5, y:9:5, abs(y-x):9:5, abs(exp(y)-2*(y-1)*(y-1)):9:5);

z:=x;

x:=y;

n:=n+1;

until (abs(x-z)<=eps) and (abs(exp(x)-2*(x-1)*(x-1))<=d);

readln;

end.

3) Модифицированный метод Ньютона:

Program P1_2_NM;

uses Crt;

var n: integer;

x0,x,eps,z,d,y,c:real;

begin

clrscr;

n:=0; x0:=-1.1; c:=-0.1; x:=x0; eps:=0.001; d:=0.01;

writeln (' n xi xi+1 xi+1-xi f(xi+1) ');

repeat

{Метод Ньютона Модифицированный}

y:=x-(exp(x)-2*(x-1)*(x-1))/(exp(x0)-4*(x0-1));

writeln (n:3, x:9:5, y:9:5, abs(y-x):9:5, abs(exp(y)-2*(y-1)*(y-1)):9:5);

z:=x;

x:=y;

n:=n+1;

until (abs(x-z)<=eps) and (abs(exp(x)-2*(x-1)*(x-1))<=d);

readln;

end.

Результаты отработки программы:

Рис.4 – программы, работающей по методу простых итераций;

Рис.5 – программы, работающей по методу Ньютона;

Рис.6 – программы, работающей по модифицированному методу Ньютона.

Рис.4 Ответ – х(11)≈0,21219

Рис.5 Ответ – х(4)≈0,21331

Рис.6 Ответ – х(10)≈0,21279