Изучение законов движения материальной точки и системы материальных точек
Лабораторные работы № 7
М и н с к 2 0 0 9
ИЗУЧЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
Основные цели и задачи. Изучение основных понятий кинематики (перемещение, скорость, ускорение) и динамики (сила, масса, импульс, механическая работа и энергия), основных законов динамики (законов Ньютона) и законов сохранения в механике.
Изучить методы измерения кинематических величин – ускорения и скорости быстродвижущихся тел. Экспериментально определить ускорение свободного падения и скорость пули из пружинного пистолета.
Механическим движением называют изменение положения в пространстве материальных тел или их частей относительно друг друга с течением времени. Одно из этих тел выделяют в качестве тела отсчета.
При описании механического движения материального тела для широкого круга задач применима модель материальной точки (МТ).
Материальная точка – это макроскопическое тело, размеры которого пренебрежимо малы по сравнению с масштабом его движения.
Если в условиях некоторой задачи протяженностью тела нельзя пренебречь, то тело можно мысленно разбить на отдельные малые элементы, каждый из которых можно рассматривать как материальную точку, т.е. представить тело как систему материальных точек. Движение такой системы в принципе может быть описано, если известен закон взаимодействия между отдельными ее элементами. В простейшем (идеальном) случае эти элементы жестко связаны между собой так, что при движении тела расстояние между любыми двумя элементами остается неизменным. Такая модель недеформируемого тела представляет собой абсолютно твердое тело и также применяется для решения широкого круга механических задач.
Движение твердого тела, при котором жестко связанная с ним прямая перемещается параллельно самой себе, называется поступательным. При поступательном движении все материальные точки, из которых состоит твердое тело, движутся одинаковым образом, и поэтому достаточно изучить движение только одной из них. Другими словами, в рамках модели материальной точки можно полностью описать поступательное движение твердого тела.
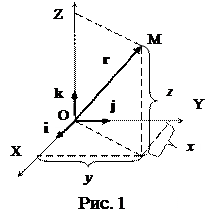
Для описания механического движения материальной точки выбирают систему отсчета, которая включает в себя тело отсчета, жестко связанную с ним систему пространственных координат[1] и часы для измерения времени. Положение материальной точки в пространстве задается с помощью ее радиуса-вектора r, который соединяет начало выбранной системы координат О с той точкой М, где в данный момент времени находится тело (рис. 1). Проекции радиуса-вектора на координатные оси есть координаты МТ:
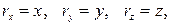 или
или  (1)
(1)
где i, j, k – орты координатных осей (векторы единичной длины вдоль осей OX, OY и OZ соответственно). При движении материальной точки ее радиус-вектор изменяется, т.е. он является функцией времени r = r (t) или в проекциях:

 x = x(t),
x = x(t),
y = y(t),
z = z(t).
Если зависимость координат от времени известна, то говорят, что задан закон движения МТ.
 Совокупность положений, последовательно
Совокупность положений, последовательно
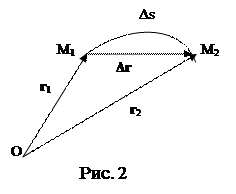
занимаемых точкой М в процессе ее движения, образует в пространстве линию, называемую траекторией движущейся точки. В общем случае траектория представляет собой некоторую кривую линию (рис. 2). Пусть в момент времени t1 точка занимает положение М1, а в момент времени t2, т.е. через промежуток времени Δt = t2 – t1 – положение М2. Расстояние Δs, которое проходит точка за время Δt, двигаясь вдоль траектории, называется путем, пройденным материальной точкой. Путь – скалярная неотрицательная величина.
Вектор Δ r, проведенный из начального положения М1 в конечное положение М2, называется перемещением точки: Δ r = r 2 − r 1. В общем случае модуль перемещения | Δ r | ипуть Δs не равны. Они совпадают лишь при прямолинейном невозвратном движении. Однако в пределе для бесконечно малого промежутка времени Δt → 0, когда Δ r → 0:
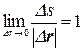 или ds = | d r |, (2)
или ds = | d r |, (2)
где знак d перед символом физической величины указывает на ее бесконечно малое изменение.
В Международной системе единиц (СИ) путь и модуль перемещения измеряются в метрах (м).
Скорость и ускорение материальной точки
Быстроту движения материальной точки характеризуют средняя скорость 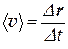 (векторная величина), (3) средняя путевая скорость
(векторная величина), (3) средняя путевая скорость 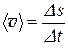 (скалярная неотрицательная величина) (4)
(скалярная неотрицательная величина) (4)
и истинная или мгновенная скорость в точке М (скорость в данный момент времени)
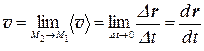 (5)
(5)
Так как единицей измерения времени в СИ является секунда (с), то скорость выражается в метрах в секунду (м/с).
Учитывая (1), для мгновенной скорости можем записать
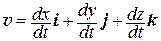 , т.е.
, т.е. 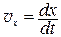 ,
, 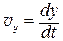 ,
, 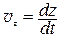 . (6)
. (6)
Мгновенная скорость v при равномерном прямолинейном движении равна средней скорости ‹ v ›, поскольку v = const. В общем случае ‹ v › характеризует движение лишь в среднем, средняя скорость эквивалентна скорости такого равномерного движения, при котором за все затраченное время тело совершило бы то же полное перемещение, как при реальном неравномерном движении. Если мгновенная скорость не изменяется по модулю (хотя может изменяться по направлению), то | v | = ‹ v ›. В любом другом случае ‹ v › характеризует скорость прохождения пути лишь в среднем.

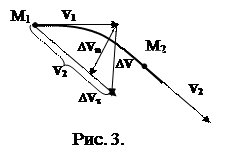 Вектор мгновенной скорости v в каждой точке траектории направлен по касательной к траектории (рис. 3). Изменение скорости за промежуток времени Δt Δ v = v 2 – v 1можно представить в виде суммы двух составляющих
Вектор мгновенной скорости v в каждой точке траектории направлен по касательной к траектории (рис. 3). Изменение скорости за промежуток времени Δt Δ v = v 2 – v 1можно представить в виде суммы двух составляющих
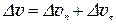 ,(7)
,(7)
первая из которых характеризует изменение мгновенной скорости по направлению (направлена перпендикулярно траектории к центру кривизны – нормальная составляющая), а вторая показывает изменение скорости по модулю (направлена по касательной к траектории по или против направления самой скорости – тангенциальная составляющая).
Величина 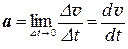 характеризует быстроту изменения скорости и носит название ускорения. В соответствии с (7) ускорение в общем случае имеет две составляющие – нормальную a n и тангенциальную a τ
характеризует быстроту изменения скорости и носит название ускорения. В соответствии с (7) ускорение в общем случае имеет две составляющие – нормальную a n и тангенциальную a τ
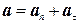 . (8)
. (8)
Так как 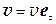 , то
, то 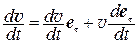 , (9)
, (9)
где v – модуль скорости, e τ – единичный вектор тангенциального направления. Последний постоянен по модулю (| e τ | = 1), но изменяется по направлению при криволинейном движении. Можно показать, что
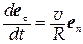 , (10) где R –радиус кривизны траектории в данной точке траектории, e n – единичный вектор нормального направления.
, (10) где R –радиус кривизны траектории в данной точке траектории, e n – единичный вектор нормального направления.
Сравнивая (8) и (9) с учетом (10), можем заключить, что
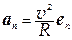 ,
, 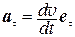 .(11)
.(11)
Из (11) видно, что нормальное ускорение отсутствует (a n = 0) при любом прямолинейном движении (R = ∞), а тангенциальное ускорение отсутствует при движении с постоянной по модулю скоростью.
Единицей измерения ускорения в СИ является метр на секунду в квадрате (м/с2).
Описание движения материальной точки с помощью введенных выше величин без выяснения причин, влияющих на это движение, составляет предмет кинематики.
Для установления закона движения материальной точки r = r (t) необходимо знать ее ускорение 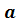 , являющееся в общем случае функцией времени, координат и скорости, а также начальные условия движения – v 0 (v при t = 0) и r 0 (r при t = 0). Закон движения находят путем интегрирования векторного дифференциального уравнения второго порядка, связывающего в общем случае ускорение, скорость, координаты и время (прямая задача). Во многих случаях бывает необходимо по известному закону движения найти скорость и ускорение материальной точки, нормальную и тангенциальную составляющие ускорения (обратная задача). Примеры решения типовых задач приведены в Приложении.
, являющееся в общем случае функцией времени, координат и скорости, а также начальные условия движения – v 0 (v при t = 0) и r 0 (r при t = 0). Закон движения находят путем интегрирования векторного дифференциального уравнения второго порядка, связывающего в общем случае ускорение, скорость, координаты и время (прямая задача). Во многих случаях бывает необходимо по известному закону движения найти скорость и ускорение материальной точки, нормальную и тангенциальную составляющие ускорения (обратная задача). Примеры решения типовых задач приведены в Приложении.
Динамика материальной точки
Если кинематика описывает то, как движется материальная точка, то динамика отвечает на вопрос, почему именно так, а не иначе, она движется, то есть рассматривает причины, определяющие характер конкретного движения. В основе динамики материальной точки лежат три закона Ньютона. Эти законы получены как результат обобщения большого числа опытных фактов и не могут быть выведены из каких-либо более общих исходных теоретических предпосылок.
 Первый закон Ньютона постулирует существование инерциальных систем отсчета – таких, относительно которых любое тело, не подверженное воздействию со стороны других тел, движется равномерно и прямолинейно. Свойство материальных тел сохранять состояние равномерного и прямолинейного движения называется инерцией. Первый закон Ньютона иначе называют законом инерции.
Первый закон Ньютона постулирует существование инерциальных систем отсчета – таких, относительно которых любое тело, не подверженное воздействию со стороны других тел, движется равномерно и прямолинейно. Свойство материальных тел сохранять состояние равномерного и прямолинейного движения называется инерцией. Первый закон Ньютона иначе называют законом инерции.
Количественной мерой инертности тела является физическая величина, носящая название массы. Единица массы в СИ – килограмм (кг), которая наряду с метром (м) и секундой (с)является основной механической единицей СИ. Единицы других механических величин являются производными от трех названных основных единиц. Заметим, что модель материальной точки в механике абстрагируется от всех других характеристик реальных тел кроме их массы. Произведение массы МТ на ее скорость называется импульсом: p = m v. Импульс, как и скорость, есть величина векторная. Импульс системы материальных точек равен векторной сумме импульсов отдельных материальных точек.
Чтобы описывать воздействия тел друг на друга вводят понятие силы. Сила – векторная величина, являющаяся мерой механического действия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет форму и размеры (деформируется). Сила F полностью задана, если указаны ее модуль F, направление в пространстве и точка приложения. Прямая, вдоль которой направлена сила, называется линией действия силы. Одновременное действие на материальную точку нескольких сил эквивалентно действию одной силы, называемой равнодействующей, или результирующей, силой и равной их геометрической сумме. Единица силы – ньютон (Н): 1 Н – сила, которая массе в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы.
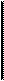 Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело силе F (при одновременном действии нескольких сил – их равнодействующей):
Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело силе F (при одновременном действии нескольких сил – их равнодействующей):
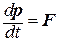 .(12)
.(12)
Это уравнение называется уравнением движения тела.
В частном случае, если масса тела в процессе движения остается постоянной, уравнение движения принимает вид:
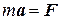 .(13)
.(13)
Уравнение движения позволяет нам выразить ускорение как функцию времени, координат и скорости, если известен характер приложенных к МТ сил, то есть получить необходимое дифференциальное уравнение для решения прямой задачи динамики.
 Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки,
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки,
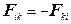 . (14)
. (14)
Силы взаимодействия всегда имеют одинаковую физическую природу.
Третий закон Ньютона позволяет перейти от динамики отдельной материальной точки к динамике произвольной системы материальных точек, поскольку позволяет свести любое взаимодействие к силам парного взаимодействия между материальными точками.
ЧАСТЬ А. Определение ускорения свободного падения с помощью машины Атвуда.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
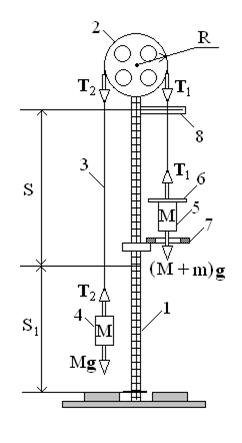
 Принципиальная схема машины А твуда показана на рис. 4. Машина состоит из вертикальной колонны 1 с линейкой с миллиметровой шкалой. В верхней части колонны укреплен легкий блок 2, свободно вращающийся вокруг горизонтальной оси. Через блок перекинута тонкая нерастяжимая нить 3, на концах которой закреплены цилиндрические грузы 4 и 5 одинаковой массы М. На правом грузе 5 устанавливается перегрузок 6 массой m, имеющий форму кольца. На колонне установлен кронштейн со съемным кольцом 7, внутренний диаметр которого больше, чем диаметр груза 5, но меньше диаметра перегрузка 6. При движении вниз груз 5 свободно проходит сквозь кольцо 7, а перегрузок 6 снимается. До снятия перегрузка система грузов движется равноускоренно, а после снятия – с постоянной скоростью. Кронштейн со съемным кольцом можно перемещать вдоль колонны, тем самым изменяя пути равноускоренного (S) и равномерного (S 1) движений груза 5, проходимых им до и после съема перегрузка. По указателю 8 устанавливают нижний срез груза 5 в исходное состояние, в котором система удерживается благодаря электромагнитному тормозу. Тормоз приводится в действие при отжатой кнопке «Пуск» на электронном приборе (на схеме не показана), блокировка снимается при ее нажатии. Прибор оснащен электронным секундомером для измерения времени равномерного движения груза 5 на отрезке пути S 1. Секундомер автоматически запускается в момент съема перегрузка благодаря тому, что в этот же момент нижний край груза перекрывает световой пучок в фотореле, выдающего на секундомер запускающий импульс, и так же автоматически останавливается при достижении грузом 5 нижней точки пути (фотореле на схеме не показаны). Предварительно до нажатия кнопки «Пуск» необходимо обнулить на табло секундомера показания предыдущего измерения кнопкой «Сброс».
Принципиальная схема машины А твуда показана на рис. 4. Машина состоит из вертикальной колонны 1 с линейкой с миллиметровой шкалой. В верхней части колонны укреплен легкий блок 2, свободно вращающийся вокруг горизонтальной оси. Через блок перекинута тонкая нерастяжимая нить 3, на концах которой закреплены цилиндрические грузы 4 и 5 одинаковой массы М. На правом грузе 5 устанавливается перегрузок 6 массой m, имеющий форму кольца. На колонне установлен кронштейн со съемным кольцом 7, внутренний диаметр которого больше, чем диаметр груза 5, но меньше диаметра перегрузка 6. При движении вниз груз 5 свободно проходит сквозь кольцо 7, а перегрузок 6 снимается. До снятия перегрузка система грузов движется равноускоренно, а после снятия – с постоянной скоростью. Кронштейн со съемным кольцом можно перемещать вдоль колонны, тем самым изменяя пути равноускоренного (S) и равномерного (S 1) движений груза 5, проходимых им до и после съема перегрузка. По указателю 8 устанавливают нижний срез груза 5 в исходное состояние, в котором система удерживается благодаря электромагнитному тормозу. Тормоз приводится в действие при отжатой кнопке «Пуск» на электронном приборе (на схеме не показана), блокировка снимается при ее нажатии. Прибор оснащен электронным секундомером для измерения времени равномерного движения груза 5 на отрезке пути S 1. Секундомер автоматически запускается в момент съема перегрузка благодаря тому, что в этот же момент нижний край груза перекрывает световой пучок в фотореле, выдающего на секундомер запускающий импульс, и так же автоматически останавливается при достижении грузом 5 нижней точки пути (фотореле на схеме не показаны). Предварительно до нажатия кнопки «Пуск» необходимо обнулить на табло секундомера показания предыдущего измерения кнопкой «Сброс».
Рассмотрим работу установки. Запишем основное уравнение динамики поступательного движения системы грузов. Сразу же учтем, что нить практически невесома и нерастяжима и потому ускорения левой и правой частей системы будут одинаковы по модулю, сила натяжения нити одинакова в любом сечении с одной стороны блока. Для правой части системы (груз 5 с перегрузком 6):
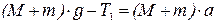 , (15)
, (15)
где Т 1– сила натяжения нити в правой части, a – модуль их ускорения, g – ускорение свободного падения.
Для левого груза 4:
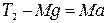 . (16)
. (16)
Запишем для блока основное уравнение динамики вращательного движения твердого тела в проекции на ось блока
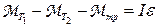 , (17)
, (17)
где 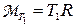 ,
, 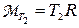 – моменты сил натяжения нити справа и слева от блока, соответственно,
– моменты сил натяжения нити справа и слева от блока, соответственно, 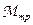 – момент сил трения, I – момент инерции блока, ε – угловое ускорение блока. Учтем, что в отсутствие проскальзывания нити
– момент сил трения, I – момент инерции блока, ε – угловое ускорение блока. Учтем, что в отсутствие проскальзывания нити 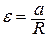 . Таким образом, получим систему уравнений
. Таким образом, получим систему уравнений
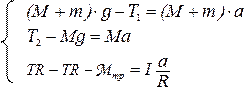 , (15'), (16'). (17')
, (15'), (16'). (17')
Решение этой системы уравнений относительно а имеет вид:
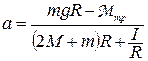 . (18)
. (18)
Поскольку трение на оси блока и момент инерции блока весьма малы
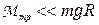 ,
, 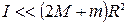 ,то выражение (18) упрощается
,то выражение (18) упрощается
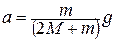 . (18')
. (18')
Следовательно, если измерить ускорение, с которым движется система грузов на участке S, то можно определить ускорение свободного падения 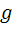 :
:
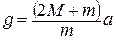 . (19)
. (19)
С целью уменьшения погрешности, которая может возникнуть из-за неточности установки системы в исходное положение ускорение определяют по измеренным пути ускоренного движения и скорости в конце этого пути (формула (П.6) приложения). Эту скорость находят по значениям пути S 1 и времени t 1 равномерного движения после снятия перегрузка. Таким образом,
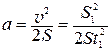
и рабочая формула для нахождения ускорения свободного падения имеет вид:
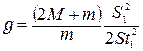 . (20)
. (20)
Значения масс используемых грузов и перегрузков: М = (64,25 ± 0,05) г; m 1 = (7,80 ± 0,05)г; m 2 = (10,50 ± 0,05)г; m 3 = (12,00 ± 0,05)г.
Задание:
1. Измерить ускорение свободного падения для трех различных масс перегрузка при значении S 1 в пределах 15…20 см. Для определения случайной погрешности измерения времени Δ t 1провести измерения 5 раз с каждым перегрузком.
2. Повторить измерения для S 1 = 25…30 см.
3. Определить абсолютную случайную погрешность измерения времени t 1 и рассчитать абсолютную погрешность определения ускорения свободного падения для каждой серии измерений.
ЧАСТЬ Б. Определение скорости полета пули с помощью крутильного баллистического маятника.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Метод баллистического маятника используется для измерения скорости быстродвижущихся тел – пуль или снарядов. В основе метода лежат законы физики абсолютно неупругого удара. Пуля массы m, летящая со скоростью v,попадает в покоящееся массивное тело-мишень массы Mм (m<<Mм) и застревает в нем. Возникающие в течение короткого промежутка времени большие диссипативные силы взаимодействия приводят к превращению большей части начальной кинетической энергии пули в тепловую энергию. Следовательно, полная механическая энергия системы пуля-мишень не сохраняется. Напротив, полный импульс этой системы сохраняется, так как названные силы для нее являются внутренними силами. Поэтому
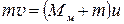 и
и 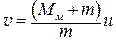 , (21)
, (21)
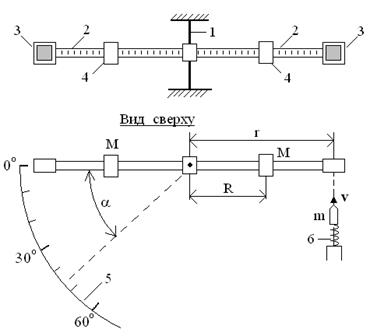 где u – скорость системы непосредственно после удара. Как видно из (21), она значительно меньше скорости пули и легко может быть измерена. Например, мишень может быть подвешена на достаточно длинной нити, т.е. представлять собой математический маятник. В нижней точке (положение равновесия) маятник приобретает скорость u, и тем самым получает запас кинетической энергии, которая при предельном отклонении маятника полностью превращается в потенциальную энергию. Измерив угол отклонения α, определяют скорость u из равенства
где u – скорость системы непосредственно после удара. Как видно из (21), она значительно меньше скорости пули и легко может быть измерена. Например, мишень может быть подвешена на достаточно длинной нити, т.е. представлять собой математический маятник. В нижней точке (положение равновесия) маятник приобретает скорость u, и тем самым получает запас кинетической энергии, которая при предельном отклонении маятника полностью превращается в потенциальную энергию. Измерив угол отклонения α, определяют скорость u из равенства
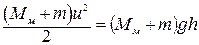 , где высота подъема маятника
, где высота подъема маятника 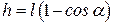 , l – длина маятника.
, l – длина маятника.
 Наибольшей компактностью с обеспечением высокой точности измерений обладает крутильный баллистический маятник. Принципиальная схема этого маятника приведена на рис. 5. На закрепленной в станине стальной струне 1 перпендикулярно к ней укреплены два стержня 2 с нанесенными через равные интервалы засечками. На концах стержней установлены две мисочки 3, заполненные пластилином. На стержнях также крепятся два перемещаемых груза 4, которые располагают симметрично относительно оси. Прибор имеет шкалу 5 для отсчета угла поворота маятника. Пуля выстреливается устройством 6, установленным напротив правой мисочки. Попадая при выстреле в мисочку и застревая в пластилине на расстоянии r от оси маятника, пуля сообщает маятнику момент импульса
Наибольшей компактностью с обеспечением высокой точности измерений обладает крутильный баллистический маятник. Принципиальная схема этого маятника приведена на рис. 5. На закрепленной в станине стальной струне 1 перпендикулярно к ней укреплены два стержня 2 с нанесенными через равные интервалы засечками. На концах стержней установлены две мисочки 3, заполненные пластилином. На стержнях также крепятся два перемещаемых груза 4, которые располагают симметрично относительно оси. Прибор имеет шкалу 5 для отсчета угла поворота маятника. Пуля выстреливается устройством 6, установленным напротив правой мисочки. Попадая при выстреле в мисочку и застревая в пластилине на расстоянии r от оси маятника, пуля сообщает маятнику момент импульса
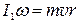 , (22) где I 1 – момент инерции маятника относительно оси вращения при положении грузов 4 на расстоянии R 1 от оси; ω – угловая скорость маятника после удара. По мере вращения маятника происходит закручивание струны и под действием момента упругих сил, возрастающего с увеличением угла закручивания, угловая скорость уменьшается до нуля. При предельном угле закручивания α потенциальная энергия достигает максимального значения.
, (22) где I 1 – момент инерции маятника относительно оси вращения при положении грузов 4 на расстоянии R 1 от оси; ω – угловая скорость маятника после удара. По мере вращения маятника происходит закручивание струны и под действием момента упругих сил, возрастающего с увеличением угла закручивания, угловая скорость уменьшается до нуля. При предельном угле закручивания α потенциальная энергия достигает максимального значения.
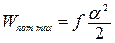 ,
,
где f – модуль кручения струны, а угол α выражен в радианах. При упругой деформации струны выполняется закон сохранения механической энергии
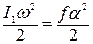 .
.
Отсюда находим начальную угловую скорость
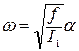 . (23)
. (23)
Подставляя выражение (23) в уравнение (22), получаем:
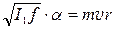 . (24)
. (24)
Расстояние r и максимальный угол отклонения маятника α легко измерить на опыте. Напротив, величины I1 и f необходимо выразить через другие величины, определенные путем прямых измерений. Если отклонить маятник на угол α и отпустить, то он будет совершать колебания с периодом
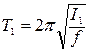 . (25)
. (25)
Умножая уравнения (24) и (25), исключим модуль кручения
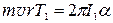 . (26)
. (26)
Момент инерции маятника можно представить следующим образом:
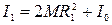 , (27) где M – масса каждого из перемещаемых грузов 4; R 1 – установленное перед стрельбой расстояние от их центров масс до оси маятника; I 0 – момент инерции не смещаемой части (стержни, мисочки, зажим).
, (27) где M – масса каждого из перемещаемых грузов 4; R 1 – установленное перед стрельбой расстояние от их центров масс до оси маятника; I 0 – момент инерции не смещаемой части (стержни, мисочки, зажим).
Чтобы исключить I 0, передвинем грузы 4 на расстояние R 2 от оси и измерим период колебаний T 2 в этом случае. При новом положении грузов момент инерции маятника равен
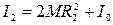 . (28) Вычитая из равенства (28) равенство (27), получаем:
. (28) Вычитая из равенства (28) равенство (27), получаем:
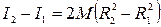 . (29) Как видно из (25):
. (29) Как видно из (25):
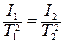
Выражая отсюда I2 через I1 и подставляя в (43), найдем:
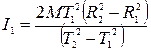 . (30) Теперь, подставляя (30) в (26), получим расчетную формулу для определения скорости полета пули
. (30) Теперь, подставляя (30) в (26), получим расчетную формулу для определения скорости полета пули
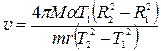 (31) Для уменьшения погрешности результата необходимо, чтобы R 1 и R 2, а, следовательно, и T 1 и T 2 отличались как можно больше, т.е. следует брать крайние положения грузов. По той же причине угол α должен быть по возможности больше. Поэтому стрельбу следует производить при минимальном расстоянии от грузов до оси вращения (т.е. при наименьшем моменте инерции маятника в целом).
(31) Для уменьшения погрешности результата необходимо, чтобы R 1 и R 2, а, следовательно, и T 1 и T 2 отличались как можно больше, т.е. следует брать крайние положения грузов. По той же причине угол α должен быть по возможности больше. Поэтому стрельбу следует производить при минимальном расстоянии от грузов до оси вращения (т.е. при наименьшем моменте инерции маятника в целом).
Значения параметров: M = (200,00±0,05)г; m =(2,00±0,05) г.
Задание:
1. Определите скорость полёта пули по серии из 5 выстрелов и рассчитайте ее абсолютную погрешность. Внимание: перед выстрелом проверяйте установку коромысла маятника на нулевую отметку угломера.
2. Повторите серию измерений при максимальном удалении грузов от оси вращения. Рассчитайте абсолютную погрешность определения скорости в этом случае и сравните ее значения в п. 1 и п. 2.
Контрольные вопросы к лабораторной работе № 7
1. Что такое средняя и мгновенная скорость?
2. Что такое ускорение? Что такое нормальное и тангенциальное ускорение?
3. Сформулировать три закона Ньютона.
4. В чем суть рассмотренного в работе метода измерения ускорения свободного падения?
5. Как создается равномерное движение двух грузов на машине Атвуда?
6. Какие упрощения были сделаны при выводе расчетной формулы для ускорения свободного падения?
7. Почему ускорение свободного падения не зависит от массы падающего тела?
8. Что представляет собой крутильный баллистический маятник?
9. В чем суть рассмотренного в работе метода определения скорости быстролетящего тела (пули)?
10. Какие законы сохранения лежат в основе работы крутильного баллистического маятника?
11. Чему равен период колебаний крутильного маятника?
12. Как рассчитывается момент инерции маятника? Какое при этом делается упрощение?
Литература
1. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. М.: Высш. шк., 2003. -541 с.
2. Савельев И.В. Курс общей физики. Учеб. пособие. В 3-х т. Т.1 Механика. Молекулярная физика. М.: Наука. Гл.ред. физ.мат. лит., 1987. – 432 с.
3. Петровский И.И. Механика. Мн.: Изд-во Белорус. ун-та, 1973.– 352 с.
4. Сивухин Д.В. Механика: Учеб. пособие для вузов. М.: Наука. Гл.ред. физ.мат. лит., 1989. – 576 с. – (Общий курс физики; Т. I)
ПРИЛОЖЕНИЕ
Действующая на материальную точку результирующая сила в общем случае может быть функцией времени, координат и скорости материальной точки – 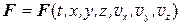 . Соответственно, функцией этих переменных является и ускорение МТ:
. Соответственно, функцией этих переменных является и ускорение МТ: 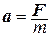 .Уравнение движения в векторном виде имеет вид
.Уравнение движения в векторном виде имеет вид
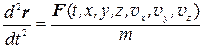 ,
,
что равносильно трем скалярным уравнениям:
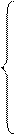
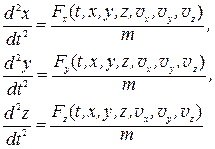 (П.1)
(П.1)
Для решения этих дифференциальных уравнений необходимо также знать начальные условия, т.е. значения координат и проекций скорости при t = 0: x 0, y 0, z 0, v x 0, v y 0, v z 0. Решение системы (П.1) в общем случае представляет сложную задачу и может быть осуществлено приближенно только численными методами с помощью компьютера. Точное аналитическое решение получается лишь в наиболее простых, но часто встречающихся на практике случаях. Рассмотрим их в порядке возрастания сложности.
1. На МТ не действуют силы либо равнодействующая приложенных сил равна нулю: F = 0 и 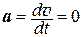 . Следовательно, v = v 0 = const, т.е. имеет место равномерное прямолинейное движение материальной точки. В этом случае наиболее рационально выбрать систему отсчета так, чтобы движение осуществлялось вдоль одной координатной оси, например, оси Oх. Тогда
. Следовательно, v = v 0 = const, т.е. имеет место равномерное прямолинейное движение материальной точки. В этом случае наиболее рационально выбрать систему отсчета так, чтобы движение осуществлялось вдоль одной координатной оси, например, оси Oх. Тогда
vх = v 0 х = v 0,а vy = vz = 0 и y = z = 0 – задача одномерная. Поскольку 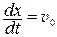 , закон движения имеет вид:
, закон движения имеет вид:
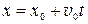 . (П.2)
. (П.2)
2. На МТ действует постоянная сила (равнодействующая сил) и потому: а = const. В этом случае возможны два варианта задачи:
2.1 Векторы а и v 0 коллинеарные. В этом случае изменение вектора скорости возможно только вдоль его начального направления и мы опять имеем одномерное (прямолинейное) движение. За положительное направление оси Oх выбираем направление вектора v 0, тогда v 0 х = v 0, vy= vz= 0, а также принимаем y = z = 0. Проекция ускорения ах на эту осьможет быть как положительной (a ↑↑ v, ах = а – ускоренное движение), так и отрицательной (a ↑↓ v, ах = – а – замедленное движение). Интегрируем:
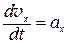 →
→ 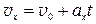 , если
, если 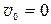 , то
, то 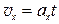 ; (П.3)
; (П.3) 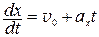 → закон движения –
→ закон движения – 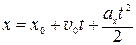 . (П.4) Если движение происходит без начальной скорости (
. (П.4) Если движение происходит без начальной скорости (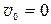 , ах = а – тело может только разгоняться), то, согласно (П.4), путь, пройденный телом за время t, равен
, ах = а – тело может только разгоняться), то, согласно (П.4), путь, пройденный телом за время t, равен 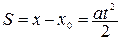 . (П.5)
. (П.5)
Отсюда ускорение а можно определить по измеренному пути и времени ускоренного движения. Если же определить скорость 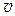 в конце равноускоренного движения, то, выразив из (П.3) время и подставив в (П.5), получим равенство
в конце равноускоренного движения, то, выразив из (П.3) время и подставив в (П.5), получим равенство 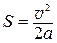 , откуда
, откуда 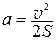 (П.6)
(П.6)
2.2 Векторы а и v 0 не коллинеарные. Векторы а и v 0 задают плоскость, в которой происходит движение тела. Выберем оси координат так, чтобы движение происходило в плоскости хOу. Ось Oу, например, направим вдоль вектора а. Тогда ах = 0, ау = а, аz = 0, т.е. а = а j, а 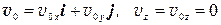 . Интегрируем:
. Интегрируем:
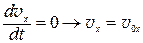
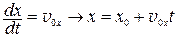 (П.7)
(П.7)
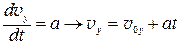 ;
; 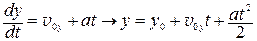 ; (П.8)
; (П.8)
z = 0
Уравнение движения получим, выразив из (П.7) время t через 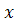 ,
, 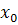 ,
, 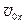 и подставив в (П.8):
и подставив в (П.8):
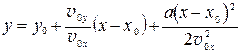 . (П.9)
. (П.9)
Траекторией является парабола. Пример – движение тела, брошенного под углом к горизонту.
[1] Чаще всего используют декартову прямоугольную систему координат
 2015-05-10
2015-05-10 546
546






