Поскольку синусоидальные токи и напряжения изображаются векторами, то, совместив начало каждого вектора с началом координат 0 комплексной плоскости, можно утверждать, что конец вектора (точка) является комплексным числом, а длина вектора (модуль комплексного числа) с учетом масштаба представляет собой величину соответствующего тока или напряжения.
Принято обозначать комплексы токов, напряжений и мощностей соответствующими буквами с точками наверху ( ), а комплексы сопротивлений и проводимостей, которые не являются гармоническими функциями времени, – подчеркиванием внизу (Z, Y).
), а комплексы сопротивлений и проводимостей, которые не являются гармоническими функциями времени, – подчеркиванием внизу (Z, Y).
Рассмотрим переход от параметрического метода расчета к символическому на примере закона Ома для цепи с последовательным соединением активного r, индуктивного xL и емкостного xC сопротивлений. Закон Ома в параметрическом методе (43) записывается в виде:
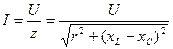 ,
,
где 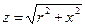 – полное сопротивление цепи (гипотенуза треугольника сопротивлений), r и соответственно x = xL − xC – активное и реактивное сопротивления цепи как катеты треугольника сопротивлений (рис.23б).
– полное сопротивление цепи (гипотенуза треугольника сопротивлений), r и соответственно x = xL − xC – активное и реактивное сопротивления цепи как катеты треугольника сопротивлений (рис.23б).
|
|
|
Угол j в треугольнике сопротивлений 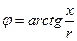 – угол сдвига по фазе между током I и напряжением U на входе цепи (рис. 23б).
– угол сдвига по фазе между током I и напряжением U на входе цепи (рис. 23б).
Предположим, что цепь имеет индуктивный характер (xL > xC) и перенесем векторную диаграмму напряжения и тока в комплексную плоскость, совместив начала векторов напряжения 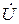 и тока
и тока  с началом 0 координат +1, +j. Очевидно концы векторов
с началом 0 координат +1, +j. Очевидно концы векторов 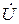 и
и  (точки) представляют собой комплексы действующих значений напряжения и тока (рис. 33).
(точки) представляют собой комплексы действующих значений напряжения и тока (рис. 33).
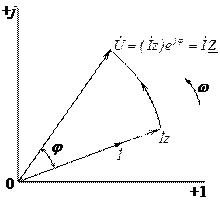
Рис. 33
Умножив вектор тока  на вещественное число (скаляр) z, получим вектор
на вещественное число (скаляр) z, получим вектор 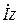 , равный по длине вектору
, равный по длине вектору 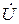 , но сонаправленный с вектором тока
, но сонаправленный с вектором тока  . Чтобы получить истинное положение вектора
. Чтобы получить истинное положение вектора 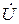 на диаграмме (рис. 33), необходимо умножить вектор
на диаграмме (рис. 33), необходимо умножить вектор 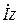 на оператор поворота ejj на угол j в положительном направлении (против часовой стрелки). Таким образом можно записать:
на оператор поворота ejj на угол j в положительном направлении (против часовой стрелки). Таким образом можно записать:
|
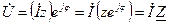 ,
,
|
– комплексное сопротивление цепи,
r = zcosj = Re Z – активное сопротивление;
x = zsinj = Im Z – реактивное сопротивления цепи.
Из равенства (68) следует: 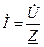 – закон Ома для последовательной цепи.
– закон Ома для последовательной цепи.
Введем понятие об эквивалентной комплексной проводимости, устранив мнимую единицу j в знаменателе
|
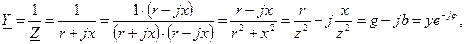
где 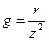 – активная проводимость;
– активная проводимость;
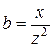 – реактивная проводимость;
– реактивная проводимость;
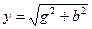 – полная (кажущаяся) проводимость эквивалентной параллель-
– полная (кажущаяся) проводимость эквивалентной параллель-
ной цепи.
Очевидно закон Ома для разветвленной (параллельной) цепи имеет вид:
|
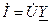 .
.
Сделаем обратный эквивалентный переход от параллельной цепи к последовательной
|
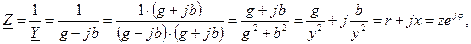
где 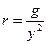 – активное сопротивление;
– активное сопротивление;
 – реактивное сопротивление;
– реактивное сопротивление;
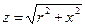 – полное (кажущееся) сопротивление эквивалентной последо-
– полное (кажущееся) сопротивление эквивалентной последо-
|
|
|
вательной цепи.
Следует обратить внимание, что при эквивалентных переходах от последовательной цепи к параллельной и наоборот знак реактивной составляющей изменяется на противоположный.
 2015-05-26
2015-05-26 1394
1394








