Число A’ называется пределом слева функции f(x) в точке a:
A’ =  ,
,
если |A’ – f(x)| < ε при 0 < a – x < δ(ε).
Аналогично, число A’’ называется пределом справа функции f(x) в точке a:
A’' = 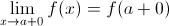 ,
,
если |A’’ – f(x)| < ε при 0 < x – a < δ(ε).
Для существования предела функции f(x) в точке a необходимо и достаточно, чтобы
f(a – 0) = f(a + 0).
17. Предел функции при стремлении аргумента к бесконечности.
Число А называется пределом функции f(x) при х ¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство
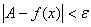
При этом предполагается, что функция f(x) определена в окрестности бесконечности.
Записывают: 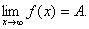
18. Основные теоремы о пределах.
А) функция не может иметь более одного предела
Б) Если функции f(x) и g(x) имеют пределы в точке 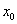 , то:
, то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
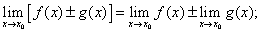
2) предел произведения функций равен произведению пределов сомножителей, т.е.


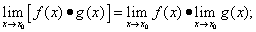
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
|
|
|
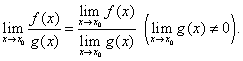
В) Если существует конечный предел, то для непрерывных функций символы предела и функции можно поменять местами.
19. Замечательные пределы.
· Первый замечательный предел:
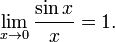
· Второй замечательный предел:
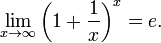
20. Бесконечно малые функции. Свойства бесконечно малых функций.
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если 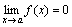 или
или 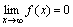 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Свойства:
· Если функции 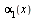 и
и 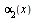 являются бесконечно малыми, то функция
являются бесконечно малыми, то функция 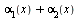 также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых.
· Произведение ограниченной при 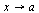 функции на бесконечно малую есть функция бесконечно малая.
функции на бесконечно малую есть функция бесконечно малая.
· Произведение постоянной на бесконечно малую есть бесконечно малая.
· Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
21. Бесконечно большие функции и их связь с бесконечно малыми.
Бесконечно большая функция - функция переменного х, которая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Функция f(x), определенная в окрестности точки х0, называется бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой:
|
|
|
Если f(x) 0 при х а (если х ¥) и не обращается в ноль, то
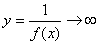
22. Сравнение бесконечно малых функций.
Пусть 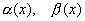 бесконечно малые функции при
бесконечно малые функции при 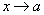 . Предположим, что существует предел их отношения и он равен l.
. Предположим, что существует предел их отношения и он равен l.
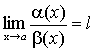 .
.
Тогда если:
1) l= 1, то функции 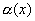 и
и 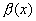 называются эквивалентными бесконечно малыми
называются эквивалентными бесконечно малыми
2) l - число, l ¹0, то функции 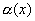 и
и 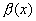 называются бесконечно малыми одинакового порядка;
называются бесконечно малыми одинакового порядка;
3) l =0, то функция 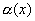 называется бесконечно малыми более высокого порядка, чем
называется бесконечно малыми более высокого порядка, чем 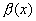 ;
;
4) l = ±¥, то функция 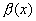 называется бесконечно малыми более высокого порядка, чем
называется бесконечно малыми более высокого порядка, чем 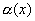 .
.
23. Свойства эквивалентных бесконечно малых. Главная часть бесконечно малой функции.
а) a ~ a, 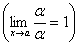
б) Если a ~ b и b ~ g, то a ~ g, 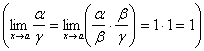
в) Если a ~ b, то b ~ a, 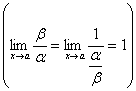
г) Если a ~ a1 и b ~ b1 и 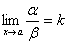 , то и
, то и 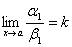 или
или 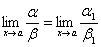 .
.
Если a и b - бесконечно малые при х а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Тогда говорят, что a - главная часть бесконечно малой функции g.
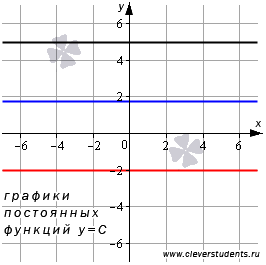
24. Свойства и графики основных элементарных функций.
а) Постоянная функция 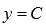
 2015-05-30
2015-05-30 4689
4689








