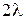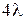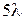11.1. Система случайных величин имеет равномерное распределение внутри квадрата со стороной a. Диагонали квадрата совпадают с осями координат. Определить: а) плотность совместного распределения вероятностей системы (X,Y);
б) плотность распределения вероятностей каждой из случайных величин, входящих в систему.
11.2. Система трех случайных величин (X, Y, Z) распределена равномерно внутри цилиндра, ось которого совпадает с осью OZ и точкой O делится пополам. Радиус цилиндра равен R, а высота 2h. Определить: а) плотность совместного распределения вероятностей системы (X, Y, Z); б) плотность распределения каждой из случайных величин, входящих в систему.
11.3. Система случайных величин (X, Y) подчинена закону распределения с плотностью распределения вероятностей 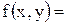
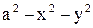 , если
, если 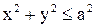 и
и 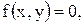 если
если 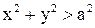 . Найти: 1) a; 2)
. Найти: 1) a; 2) 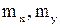 ; 3)дисперсии
; 3)дисперсии 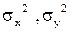 ;
;
11.4. Система двух случайных величин (X,Y) подчинена нормальному закону распределения. Рассеивание круговое. Найти вероятность попадания случайной точки (X, Y) в круг, центр которого cовпадает с центром рассеивания, а радиус равен двум вероятным отклонениям (Вероятное отклонение 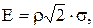 где
где
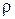 = 0,476936).
= 0,476936).
11.5. Плотность совместного распределения вероятностей системы случайных величин X,Y имеет вид: 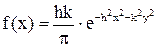 , где
, где 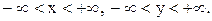 Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
Определить параметры распределения. Выяснить, зависимы или независимы случайные величины X, Y.
11.6. Плотность совместного распределения системы случайных величин X, Y:
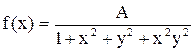 . Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
. Найти коэффициент A. Найти законы распределения случайных величин X, Y. Установить, зависимы или нет случайные величины X, Y.
11.7. Система двух случайных величин (X, Y) подчинена закону распределения с плотностью совместного распределения: 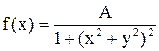 . Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
. Определить коэффициент A и найти радиус круга с центром в начале координат, вероятность попадания в который равна P.
11.8. Система случайных величин (X,Y) имеет плотность совместного распределения
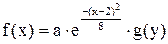 , где
, где 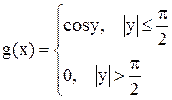 . Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
. Найти a. Написать выражение плотностей распределения случайных величин X и Y. Определить математические ожидания и дисперсии случайных величин X и Y.
11.9. Производится единичное бомбометание по прямоугольной наземной цели. Ширина цели равна 20 м, а длина 100 м. Прицеливание по центру цели. Оси рассеивания совпадают с направлением полета и с перпендикуляром к этому направлению. Вероятное отклонение в направлении полета равно 60 м, в направлении, перпендикулярном полету – 40 м. Систематические ошибки отсут-ствуют. Вероятность попадания в цель при сбрасывании одной бомбы. Указание: Вероятное отклонение 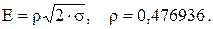
11.10. Плотность совместного распределения системы случайных величин X, Y равна 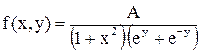 . Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
. Определить A. Найти функции распределения и плотности распределения случайных величин, входящих в систему. Определить, зависимы или независимы случайные величины: X, Y.
11.11. Дана плотность совместного распределения случайных величин X, Y:
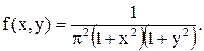 Определить вероятность попадания в прямоугольник:
Определить вероятность попадания в прямоугольник:
 y
y
 (2;1,5)
(2;1,5)
 (0;-1) (2;-1) х
(0;-1) (2;-1) х
11.12. Система случайных величин (X, Y) распределена с постоянной плот-ностью внутри квадрата. Найти плотности распределения случайных величин X, Y входящих в систему:
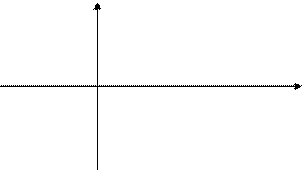 y
y
 1
1
-1 1 x
-1
11.13. Система случайных величин (X, Y) подчинена закону распределения с плотностью:
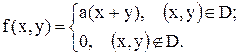
Область D - квадрат, ограниченный линиями x = 0; x = 3; y = 0; y = 3.
Найти: а) Коэффициент a; б) вероятность попадания случайной точки (x, y) в квадрат, ограниченный прямыми x = 1, x = 2, y = 1, y = 2; в) 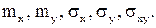
11.14. Определить плотность распределения вероятностей, математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если 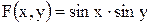 ,
, 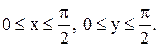
11.15. Плотность совместного распределения случайных величин (X,Y): 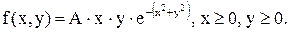 Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
Определить: 1) коэффициент A; 2) законы распределения каждой из случайных величин, входящих в систему; 3) математичес-
кие ожидания каждой из случайных величин.
11.16. Плотность совместного распределения системы случайных величин X, Y равна 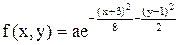 . Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
. Найти коэффициент a. Установить, являются ли величины зависимыми. Определить вероятность совместного выполнения двух неравенств x < -3; y < 4.
11.17. Координаты случайной точки (X,Y) раcпределены равномерно внутри прямоугольника, ограниченного прямыми x = 0, x = a, y = 0, y = b. Определить вероятность попадания случайной точки в круг радиуса R = a,если a > b, а центр круга совпадает с началом координат.
11.18. Координаты (X, Y) случайной точки распределены равномерно внутри прямоугольника, ограниченного прямыми x = a, x = b, y = c, y = d (в > a, d > c). Найти плотность распределения вероятностей и функцию распределения системы случайных величин X, Y. Выяснить, являются ли X, Yнезависимыми величинами.
11.19. Плотность совместного распределения случайных величин X, Y равна:
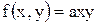 в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми
в области D и f(x,y)=0 вне этой области. Область D- треугольник, ограниченный прямыми 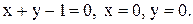 Найти а)
Найти а) 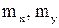 ; б) коэффициент корреляции
; б) коэффициент корреляции 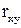 , дисперсии
, дисперсии 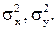
11.20. Плотность совместного распределения системы случайные величины
(X, Y), заданной внутри круга радиуса R, равна 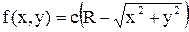 . Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
. Опреде-лить: 1) постоянную C; 2) вероятность попадания в круг радиуса a < R, если центры обоих кругов совпадают с началом координат.
11.21. Плотность совместного распределения системы случайных величин
(X, Y): 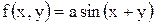 в области D и
в области D и 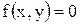 вне этой области. Область D определяется неравенствами
вне этой области. Область D определяется неравенствами 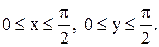 Определить: a) постоянную a;
Определить: a) постоянную a;
б) 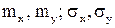 ; в) определить коэффициент корреляции r xy.
; в) определить коэффициент корреляции r xy.
11.22. Дана плотность совместного распределения системы случайных величин 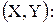
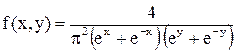 . Определить вероятность попадания случайной точки (x, y)в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
. Определить вероятность попадания случайной точки (x, y)в прямоугольник с вершинами в точках (0; 0), (1; 0), (0; 1), (1; 1).
11.23. Плотность распределения вероятностей двумерного случайного вектора (X, Y)имеет следующий вид: 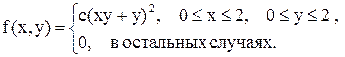 .
.
Вычислить: а) значение постоянной c; б) вероятность 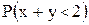 ); в) центр рассеивания.
); в) центр рассеивания.
11.24. Случайные величины X и Y независимы и распределены каждая по показательному закону с параметрами соответственно l1 и l2. Найти вероятность 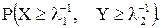
11.25. Функция совместного распределения двух случайных величин X и Y имеет следующий вид:
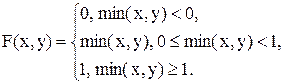
Найти одномерные законы распределения компонент и решить вопрос об их зависимости или независимости.
11.26. Случайные величины X и Y независимы и распределены следующим образом: X - по закону N(1; 2), Y - по равномерному закону на отрезке [0; 2].
Найти вероятность следующих событий: 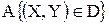 , где область
, где область
D = {(x,y) / (0 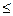 x
x 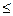 2, 0
2, 0 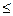 y
y 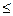 1); B = {X > Y}.
1); B = {X > Y}.
11.27. Случайная точка на плотности (X,Y) распределена по круговому нормальному закону (rxy = 0, sx = sy = s = 1,) с центром рассеивания в начале координат. Вычислить вероятности следующих событий: A = {Y > X},
B = {çYç> X}, C = {Y < 3X}, D = {çXç < 1}, E = {X < 1, Y < 2}.
11.28. Заданы следующие характеристики двумерного нормального вектора:
mx = -2; my = 3 и ковариационная матрица 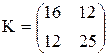 . Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2sx, b = 2sy.
. Записать выражение для плотности распределения вероятностей f(x, y) и вычислить вероятность попадания в эллипс рассеивания с полуосями a = 2sx, b = 2sy.
11.29. Определить вероятность попадания точки с координатами (X, Y) в область, определяемую неравенствами (1 £ X £ 2, 1 £ Y £ 2), если функция распреде-ления 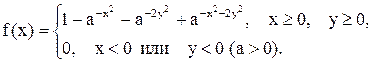
11.30. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения вероятностей 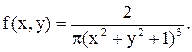
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ
Задача 1. На рис. 1 и 2 изображены электрические схемы. Выключатели изображены кружками, в которых указан номер выключателя. Записать через события 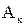 - «включен выключатель с номером
- «включен выключатель с номером 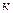 » для каждой схемы следующие события:
» для каждой схемы следующие события: 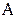 - «ток идет» и
- «ток идет» и 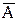 - «ток не идет».
- «ток не идет».
 |
Рис. 1 Рис. 2
Решение. В схеме, приведенной на рис. 1, ток идет, если включены или 1 и 3 выключатели, или выключатель 2. Эти события соответственно равны 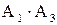 и
и 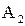 . Поэтому событие
. Поэтому событие 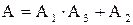 . В схеме (рис. 1) ток не идет, если выключены выключатель 2 и хотя бы один из выключателей 1 или 3. Эти события соответственно равны
. В схеме (рис. 1) ток не идет, если выключены выключатель 2 и хотя бы один из выключателей 1 или 3. Эти события соответственно равны 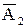 и
и 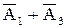 . Поэтому событие
. Поэтому событие 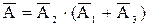 . Иначе, используя свойства операций над событиями,
. Иначе, используя свойства операций над событиями,
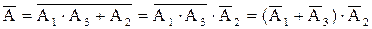 .
.
Для схемы (рис. 2) 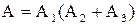 ,
, 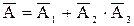 .
.
Задача 2. Наудачу взятый телефонный номер состоит из пяти цифр. Как велика вероятность, что в нем: а) все цифры различные; б) все цифры нечетные?
Решение. а) Событие 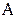 - все цифры различные.
- все цифры различные. 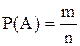 , где
, где 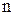 - число всех элементарных равновозможных событий, m - число элементарных равновозможных событий, благоприятных наступлению события
- число всех элементарных равновозможных событий, m - число элементарных равновозможных событий, благоприятных наступлению события 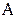 . Пусть
. Пусть 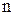 - число всевозможных способов выбора 5 цифр из 10 возможных, причем цифры могут повторяться, поэтому
- число всевозможных способов выбора 5 цифр из 10 возможных, причем цифры могут повторяться, поэтому 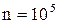 . m - число всевозможных способов выбора 5 цифр из 10 возможных, но цифры должны быть различными, поэтому
. m - число всевозможных способов выбора 5 цифр из 10 возможных, но цифры должны быть различными, поэтому 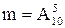 (порядок для телефонного номера важен). Таким образом,
(порядок для телефонного номера важен). Таким образом, 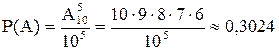 .
.
б) Событие 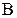 - все цифры нечетные.
- все цифры нечетные. 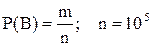 ,
, 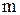 - число всевозможных способов выбора 5 цифр из 5 нечетных, причем цифры могут повторяться, поэтому
- число всевозможных способов выбора 5 цифр из 5 нечетных, причем цифры могут повторяться, поэтому 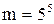 . Таким образом,
. Таким образом, 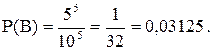
Задача 3. Некто написал 3 письма, запечатал их в конверты, а затем наудачу на каждом из них написал различные адреса. Определить вероятность того, что хотя бы на одном из конвертов написан правильный адрес.
Решение. Пусть событие 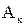 состоит в том, что на k-м конверте написан правильный адрес (
состоит в том, что на k-м конверте написан правильный адрес (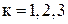 ). Искомая вероятность
). Искомая вероятность 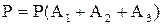 , так как события А1, А2, А3 совместны, то
, так как события А1, А2, А3 совместны, то
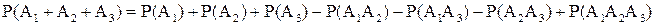 .
.
Для всех 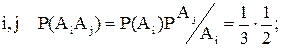
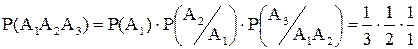 . Таким образом,
. Таким образом,
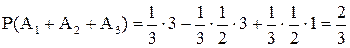 .
.
Задача 4. Три станка подают детали в общий бункер. Вероятность выпуска бракованной детали для первого станка равна 0,03, для второго – 0,02 и для третьего – 0,01. Производительность первого станка в три раза больше производительности второго, а производительность третьего станка в два раза больше производительности второго. Какова вероятность того, что взятая наудачу из бункера деталь будет бракованной?
Решение. Пусть событие 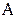 - деталь, взятая наудачу из бункера, бракованная. Событие
- деталь, взятая наудачу из бункера, бракованная. Событие 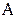 может произойти только совместно с одним из следующих событий:
может произойти только совместно с одним из следующих событий: 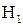 - деталь изготовлена на 1-м станке,
- деталь изготовлена на 1-м станке, 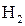 - на 2-м станке,
- на 2-м станке, 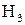 - на 3-м станке. События
- на 3-м станке. События 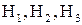 образуют полную группу несовместных событий, поэтому
образуют полную группу несовместных событий, поэтому
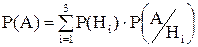 . Если принять производительность второго станка за k, то производительность первого станка - 3k, третьего – 2k. Тогда
. Если принять производительность второго станка за k, то производительность первого станка - 3k, третьего – 2k. Тогда 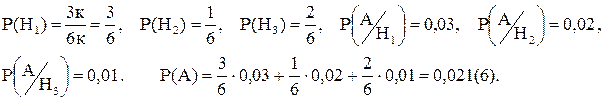

Задача 5. Найти вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%.
Решение. Пусть событие 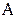 - бракованных изделий окажется более трех.
- бракованных изделий окажется более трех.
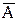 - бракованных изделий не более трех.
- бракованных изделий не более трех.
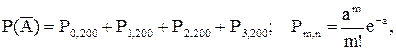 где
где 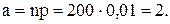
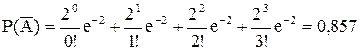 .
.
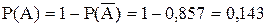 .
.
Задача 6. Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 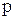 . Рассматриваются случайные величины:
. Рассматриваются случайные величины:
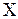 - разность между числом попаданий и числом промахов;
- разность между числом попаданий и числом промахов; 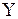 - сумма числа попаданий и числа промахов. Построить для каждой из случайных величин
- сумма числа попаданий и числа промахов. Построить для каждой из случайных величин 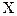 ,
, 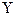 ряд распределения. Найти их характеристики
ряд распределения. Найти их характеристики 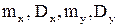 .
.
Решение. Случайная величина 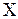 может принимать следующие значения:
может принимать следующие значения: 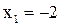 (0 попаданий, 2 промаха),
(0 попаданий, 2 промаха), 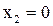 (1 попадание, 1 промах),
(1 попадание, 1 промах), 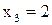 (2 по-падания, 0 промахов). Вероятности значений случайной величины
(2 по-падания, 0 промахов). Вероятности значений случайной величины 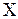 находятся по формуле Бернулли:
находятся по формуле Бернулли: 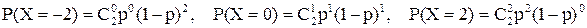 .
.
Ряд распределения будет иметь вид
| Х | -2 | ||
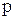 | 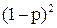 | 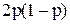 | 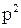 |
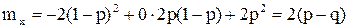 ,
,
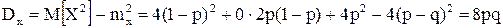 .
.
 Случайная величина
Случайная величина 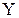 может принимать только одно значение: два с вероятностью, равной единице
может принимать только одно значение: два с вероятностью, равной единице 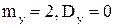 .
.

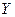 2
2
 1
1
Задача 7. Дана функция 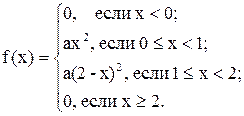
При каком значении 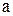 функция
функция 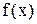 является плотностью распределения случайной величины
является плотностью распределения случайной величины 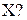 Найти функцию распределения случайной величины
Найти функцию распределения случайной величины 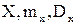 .
.
Решение. Из основного свойства плотности следует
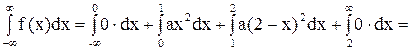
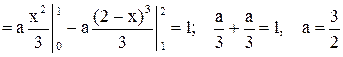 .
.
Для 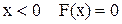 .
.
Для 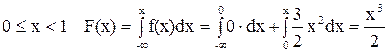 .
.
Для 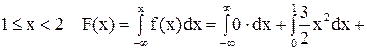
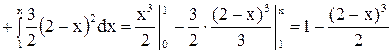 .
.
Для 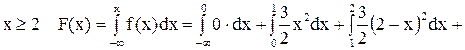
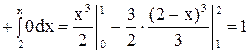 .
.
Таким образом, 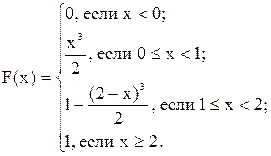
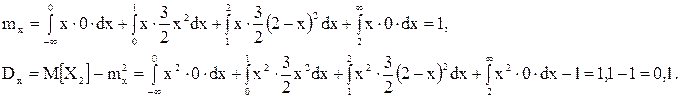
Задача 8. Время T между двумя сбоями ЭВМ распределено по показательному закону с параметром 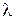 :
: 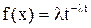 при
при 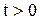 . Решение определенной задачи требует безотказной работы машины в течение времени
. Решение определенной задачи требует безотказной работы машины в течение времени 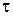 . Если за время
. Если за время 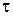 произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время
произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время 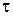 после начала решения задачи. Рассматривается случайная величина
после начала решения задачи. Рассматривается случайная величина 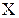 - время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи).
- время, за которое задача будет решена. Найти ее закон распределения и математическое ожидание (среднее время решения задачи).
Решение. Случайная величина 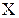 может принимать следующие значения:
может принимать следующие значения: 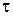 (за время
(за время 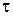 не произошло сбоя), 2
не произошло сбоя), 2 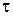 (на первом промежутке
(на первом промежутке 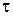 сбой произошел, на втором промежутке
сбой произошел, на втором промежутке 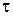 сбоя не было), 3
сбоя не было), 3 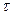 (на первых двух промежутках длины
(на первых двух промежутках длины 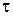 сбои происходили, на третьем сбоя не было) и т. д.
сбои происходили, на третьем сбоя не было) и т. д.
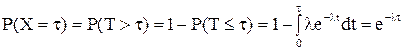 .
.
Обозначим 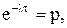 тогда
тогда 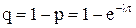 - вероятность того, что за время
- вероятность того, что за время 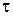 сбой произошел;
сбой произошел; 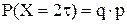 ,
, 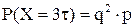 и т. д.
и т. д.



 Ряд распределения случайной величины
Ряд распределения случайной величины 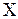

 Х
Х 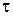 2
2 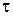 ...
... 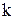
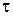 ...
...
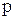
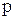
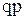 ...
... 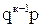 ...
...
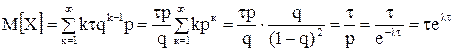 (вычисление суммы ряда
(вычисление суммы ряда 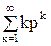 смотри методические указания к проведению практических занятий по теории вероятностей, часть 2, стр. 15).
смотри методические указания к проведению практических занятий по теории вероятностей, часть 2, стр. 15).
Задача 9. Известно, что детали, выпускаемые по размерам диаметра, распре-деляются по нормальному закону. Параметры этого закона 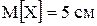 ,
, 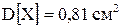 . Найти вероятность того, что диаметр наудачу взятой детали имеет размеры в пределах от 4 до 7 см.
. Найти вероятность того, что диаметр наудачу взятой детали имеет размеры в пределах от 4 до 7 см.
Решение. 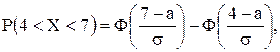 где
где 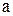 - математическое ожидание,
- математическое ожидание, 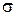 - среднее квадратическое отклонение. Таким образом,
- среднее квадратическое отклонение. Таким образом, 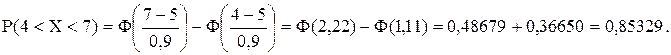



|
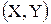
 задан таблицей:
задан таблицей:

 |
Найти: а) 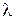 ; б) частные законы распределения случайных величин
; б) частные законы распределения случайных величин 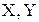 ;
;
в) 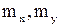 ,
, 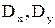 ; г) коэффициент корреляции
; г) коэффициент корреляции 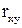 ; д) вероятность попаданий
; д) вероятность попаданий
двумерной случайной величины в область 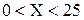 ;
; 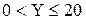 .
.
Решение: так как 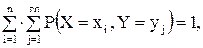
то 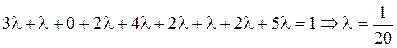 .
.
Закон распределения случайной величины X

 Х 10 20 30
Х 10 20 30
Р 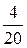
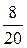
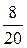 , т. к.
, т. к. 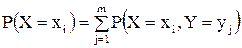 .
.
Закон распределения случайной величины Y
 Y 20 40 60
Y 20 40 60
P 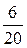
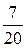
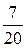 .
.
Отсюда:
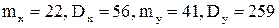
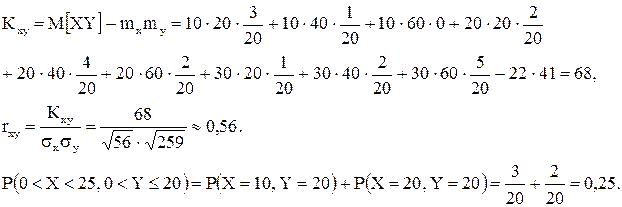
Задача 11. Плотность совместного распределения системы двух случайных величин 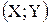 задана выражением
задана выражением 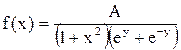 .
.
Найти: а) коэффициент А; б) плотности распределения случайных величин 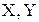 , входящих в систему; в) определить зависимы или независимы случайные величины.
, входящих в систему; в) определить зависимы или независимы случайные величины.
Решение. Из основного свойства плотности
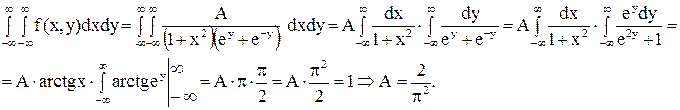
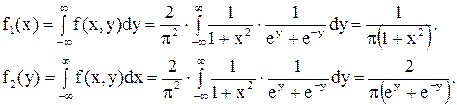
Т.к. 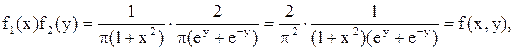
случайные величины 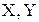 - независимы.
- независимы.
 2015-06-10
2015-06-10 6125
6125
 0 20
0 20