Гидростатическое давление обладает двумя основными свойствами.
1-ое свойство. Силы гидростатического давления в покоящейся жидкости всегда направлены внутрь по нормали к площадке действия, т.е. являются сжимающими.
Это свойство доказывается от противного. Если предположить, что силы направлены по нормали наружу, то это равносильно появлению в жидкости растягивающих напряжений, которых она воспринимать не может (это вытекает из свойств жидкости).
2-ое свойство. Величина гидростатического давления в любой точке жидкости по всем направлениям одинаково, т.е. не зависит от ориентации в пространстве площадки, на которую оно действует
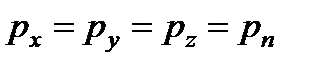 ,
,
где 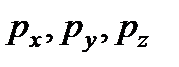 - гидростатические давления по направлению координатных осей;
- гидростатические давления по направлению координатных осей;
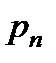 - то же по произвольному направлению
- то же по произвольному направлению 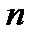 .
.
Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными 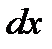 ,
, 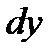 и
и 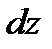 (рис. 2.3).
(рис. 2.3).
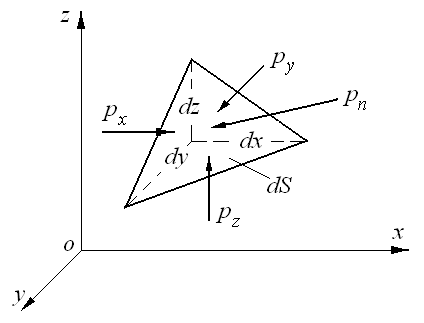
Рис. 2.3. Схема для доказательства свойства
о независимости гидростатического давления от направления
Введем обозначения: 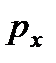 -гидростатическое давление, действующее на грань, нормальную к оси
-гидростатическое давление, действующее на грань, нормальную к оси 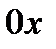 ;
;
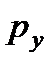 - давление на грань, нормальную к оси
- давление на грань, нормальную к оси 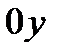 ;
;
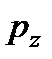 - давление на грань, нормальную к оси
- давление на грань, нормальную к оси 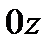 ;
;
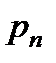 - давление, действующее на наклонную грань;
- давление, действующее на наклонную грань;
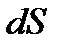 - площадь этой грани;
- площадь этой грани;
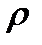 - плотность жидкости.
- плотность жидкости.
Запишем условия равновесия для тетраэдра (как для твердого тела) в виде трех уравнений проекций сил и трех уравнений моментов:
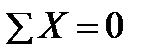 ,
, 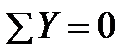 ,
, 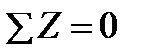 ;
;
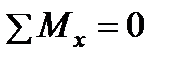 ,
, 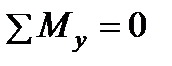 ,
, 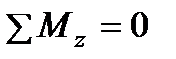 .
.
При уменьшении в пределе объема тетраэдра до нуля система действующих сил преобразуется в систему сил проходящих через одну точку, и, таким образом, уравнения моментов теряют смысл.
Таким образом, внутри выделенного объема на жидкость действует единичная массовая сила, проекции ускорений которой равны 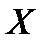 ,
, 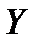 ,и
,и 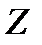 . В гидравлике принято массовые силы относить к единице массы, а так как
. В гидравлике принято массовые силы относить к единице массы, а так как 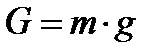 , то проекция единичной массовой силы численно будет равна ускорению.
, то проекция единичной массовой силы численно будет равна ускорению.
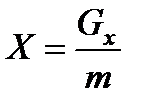 ;
; 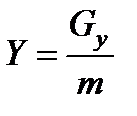 ;
; 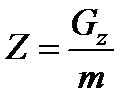 ,
,
где 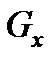 ,
, 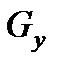 ,
, 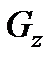 - проекции единичной массовой силы на оси координат;
- проекции единичной массовой силы на оси координат;
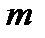 - масса жидкости;
- масса жидкости;
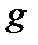 - ускорение.
- ускорение.
Составим уравнение равновесия выделенного объема жидкости в направлении оси 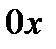 , учитывая при этом, что все силы направлены по нормалям к соответствующим площадкам внутрь объема жидкости:
, учитывая при этом, что все силы направлены по нормалям к соответствующим площадкам внутрь объема жидкости:
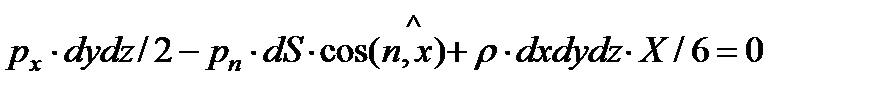 , (2.4)
, (2.4)
где 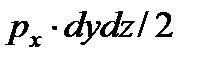 - проекция силы от гидростатического давления
- проекция силы от гидростатического давления 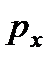 ;
;
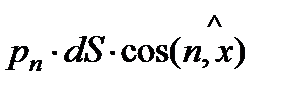 - проекция силы от давления
- проекция силы от давления 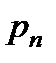 ;
;
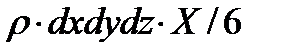 - проекция массовой силы, действующей на тетраэдр.
- проекция массовой силы, действующей на тетраэдр.
Разделив уравнение (2.2) на площадь 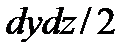 , которая равна площади проекции наклонной грани
, которая равна площади проекции наклонной грани 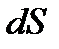 на плоскость
на плоскость 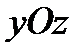 , т. е.
, т. е. 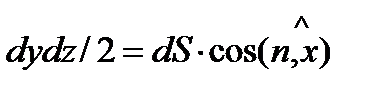 , получим
, получим
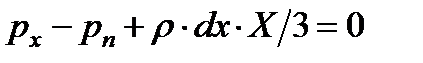 .
.
При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель 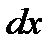 , также стремится к нулю
, также стремится к нулю 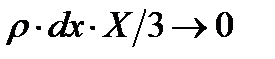 , а давления
, а давления 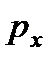 и
и 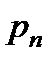 остаются величинами конечными.
остаются величинами конечными.
Следовательно, в пределе получим
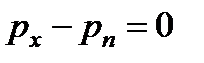 или
или 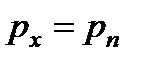 .
.
Аналогично составляя уравнения равновесия вдоль осей 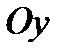 и
и 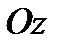 , находим
, находим
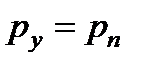 ,
, 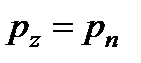 ,
,
или 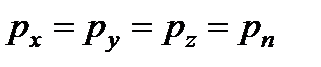 .
.
Так как размеры тетраэдра 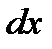 ,
, 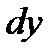 и
и 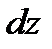 и наклон площадки
и наклон площадки 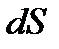 взяты произвольно, то, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Что и требовалось доказать.
взяты произвольно, то, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково. Что и требовалось доказать.
Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой (идеальной) жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.
В общем случае давление в точке зависит от координат рассматриваемой точки, а при неустановившемся движении жидкости может изменяться в каждой данной точке с течением времени: 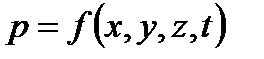 .
.
 2015-06-04
2015-06-04 2492
2492








