Предположим, что проведены диагностические испытания умственного развития у школьников шестых классов городской и сельской школ: можно ли в дальнейшем рассматривать обе школьные выборки как принадлежащие одной совокупности? По поводу неодинаковых условий обучения в городской и сельской школах высказано немало противоречивых суждений. Психолог в данном случае намерен опираться на экспериментальные факты. Чтобы прийти к какому-то решению, целесообразно проанализировать полученный экспериментальный материал. Это достаточно часто встречающаяся задача, но есть и такие, где приходится отвечать на один и тот же вопрос относительно нескольких, а не двух выборок. Именно в таком случае мы имеем дело с задачей второго типа.
Перед психологом два ряда численностей. Положим, что оба ряда имеют распределение, близкое к нормальному. Сравнение величин центральных тенденций – в данном случае их представляют средние арифметические – не даст ответа на вопрос о том, относятся ли выборки к одной совокупности. Почти безошибочно можно утверждать, что средние арифметические не будут тождественными, но этого явно недостаточно для ответа на поставленный вопрос, ответ не будет получен, даже если средние арифметические окажутся равными. Для данного случая более всего подходит сравнение выборок по t-критерию Стъюдента.
|
|
|
Перед тем как ознакомиться с техникой вычислений и интерпретацией результатов, получаемых при работе с t-критерием Стьюдента, необходимо остановиться на некоторых статистических терминах; они постоянно встречаются в прикладной статистике,
В том разделе статистики, где заходит речь о проверке гипотез, постоянно приходится иметь дело с нуль-гипотезой, или нулевой гипотезой. При сравнении двух выборок нуль-гипотеза формулируется следующим образом:между изучаемыми выборками нет различия или, иначе, различие между ними несущественно. Все дальнейшие расчеты направлены на то, чтобы прийти к заключению: верна ли нуль-гипотеза или от нее нужно отказаться, и в действительности существенная разница между выборками имеется, В других случаях, в зависимости от содержания материала, меняются формулировки, но вычисления показываю, какова вероятность нуль-гипотезы. Для обозначения нуль-гипотезы используется символ Н0.
Допустим, что разница между выборками имеется. Исследователь встает перед вопросом: насколько существенна эта разница, как часто будет обнаруживаться она в последующем, когда придется работать с подобными выборками. Самые общие соображения при этом таковы: если разница получена на небольшом материале (числе случаев, охваченных той или другой выборкой), то при повторном изучении таких же выборок разницу, возможно, найти и не удастся. Другое дело, если изучаемые выборки немалы. Далее важно, оказалась ли обнаруженная разница значительной. Это рассуждение и следует иметь в виду, когда в статистике речь идет об уровне значимости полученного коэффициента, параметра и пр. Уровни значимости представлены в специальных таблицах, которые обычно даются в учебниках статистики, есть такие таблицы и в конце этой книги (см. Приложение 3).
|
|
|
Какой уровень значимости можно признать удовлетворительным?
В психологии и педагогике минимально допустимым для отказа от Н0 уровнем значимости признается 0,95. Это значит; что расчеты, основанные на математической теории вероятности, дают основание утверждать, что при проведении таких же исследований, по крайней мере в 95%, будет получен такой же результат; возможно, лишь с несущественными отклонениями. В некоторых работах удается получить и более высокие уровни значимости – 0,99 и даже 0,999 (эти же уровни значимости можно записать в виде 0,05; 0,01; 0,001. Записывая уровень 0,95, имеют в виду, что полученные параметры повторяются в 95% случаев, а записывая 0,05, что в 5% случаев они не повторяются, смысл в том и другом случае один и тот же).
А если не получен уровень значимости 0,95?
Тогда нужно признать, что нуль-гипотезу не следует отвергать. Впрочем, иногда по задачам исследования признается достаточным и более низкий уровень. В некоторых исследованиях цель состоит в том, чтобы прийти к утверждению нуль-гипотезы.
Обращаясь к таблицам уровней значимости, исследователь обнаруживает во многих из них специальный столбец с указанием степеней свободы, относящихся к полученному параметру или коэффициенту. Уровень значимости прямо зависит от того, каким числом степеней свободы обладает данный коэффициент или параметр. Число независимых величин, участвующих в образовании того или другого параметра, называется числом степеней свободы этого параметра. Оно равно общему числу величин, по которым вычисляется параметр, минус число условий, связывающих эти величины. Числа степеней свободы и способы его определения всегда даются в окончательных формулах, которыми пользуется исследователь при статистической обработке своих материалов.
Рассмотрим пример с двумя выборками (см. табл. 3 и 4), которые, по мнению исследователя, можно рассматривать как подлежащие обработке параметрическим методом.
Двум группам шестиклассников по 6 человек в каждой было дано задание бросать мяч в корзину. Группы обучались по разным программам.
Можно ли считать, что разница в программах сказалась на конечной результативности школьников?
Для сравнения было взято число попаданий в корзину. Всего было дано по 10 проб. Формула вычисления t:
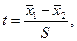 где
где 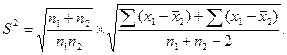
Материал, подлежащий обработке, приведен в табл. 3 и 4.
Таблица 3
Данные 1-й выборки, n = 6
| Исп. | x | x – 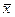
| (x – 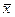 )2 )2
|
| А | –1 | ||
| Б | |||
| В | |||
| Г | |||
| Д | –2 | ||
| Е | –2 |
Σx=18; Σ(x- 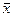 )2=20;
)2=20; 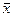 =3
=3
Таблица 4
Данные 2-й выборки, n = 6
| Исп. | x | x – 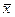
| (x – 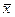 )2 )2
|
| Ж | – | – | |
| З | –1 | ||
| И | –3 | ||
| К | |||
| Л | |||
| М | – | – |
Σx=30; Σ(x- 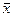 )2=20;
)2=20; 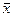 =5
=5
Ход вычислений показывает:
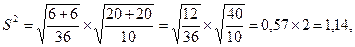
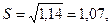
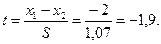
число степеней свободы fd = n1+n2-2=10.
По таблице уровней значимости t-распределения Стьюдента (см. Приложение 3, табл. 1) находим при 10 степенях свободы t0,05 =2,228.
Существенность различия не доказана, хотя полученное значение t=1,9 близко к требуемому уровню. Принимается Н0.
Нельзя утверждать, что выборки существенно отличаются одна от другой. Для вычисления t существует несколько формул, различающихся только техникой расчетов.
Нужно заметить, что сравниваемые выборки могут быть неодинаковыми по объему. Применять параметрические методы можно лишь к материалу, обладающему определенными свойствами, о которых говорилось ранее. В других случаях следует обращаться к непараметрическим методам.
|
|
|
Ниже будет рассмотрена техника применения критерия Манна – Уитни, непараметрического метода, часто используемого в психологических исследованиях.
Предположим, что психологу нужно решить такую задачу: есть ли различия между выборками школьников одного и того же класса; одна выборка включает школьников, которые до контрольной работы проходили дополнительное обучение по коррекционным программам, другая – школьников, такого обучения не проходивших. Обе выборки малы, поэтому для проверки гипотез о существовании различия между выборками следует взять мощный критерий; мощность критерия – это вероятность принятия при его применении правильного решения для отклонения Н0; чем выше эта вероятность, тем больше мощность критерия. Мощность любого критерия увеличивается вместе с увеличением объема сравниваемых выборок, а также со снижением того уровня значимости, на который ориентируется исследователь. Другими словами, если выборки велики, то принятие правильного решения относительно Н0 увеличивается. Ориентация на высокий уровень значимости, например 0,99 или 0,999, предполагает применение достаточно мощного критерия. В рассматриваемом примере выборки малы, а при установлении существенной разницы между ними, т.е. при отказе от Н0, желательно, чтобы уровень значимости был как можно выше, но не ниже 0,95. Формула вычисления критерия Манна – Уитни такова:
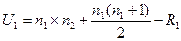 и
и 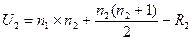
В примере сравнению подлежат результаты контрольной работы выборки А, состоящей из четырех школьников, проходивших обучение по коррекционным программам, и выборки Б, состоящей из семи школьников, никакого коррекционного обучения не проходивших (см. табл. 5 и 6). Последовательность действий, предусматриваемых вычислением всех нужных для решения задачи величин, такова:
- выписать в любом порядке число успешно решенных заданий школьниками сначала выборки А, затем выборки Б;
- проранжировать число успешно решенных заданий, объединив обе выборки;
- найти сумму рангов выборок А и Б раздельно. Эти три действия дадут все необходимые для вычисления критерия данные.
Таблица 5
|
|
|
 2015-06-14
2015-06-14 867
867








