Как правило, при изготовлении продукции на процесс её производства оказывает влияние множество различных факторов, в результате чего наблюдается разброс значений показателей качества продукцию. Таким образом, показатели качества изготовляемой продукции или оказываемых услуг следует рассматривать как случайные величины.
Случайной величиной называется такая величина, которая в результате испытаний в границах определенного интервала может принимать различные числовые значения (согласно СТБ ГОСТ Р 50779.10 случайная величина - переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей).
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные значения и не могут принимать значения промежуточные между ними. Например, количество негодных деталей в партии может быть только целым положительным числом 1, 2, 3 и т.д., но не может быть 1,3; 1,7 и т.п.
|
|
|
Непрерывной случайной величиной называется такая величина, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.
Например, действительные размеры деталей, обработанных на станке, являются случайными величинами непрерывного типа, так как они могут принять любое численное значение в определенных границах.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей.
Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей для каждого из значений, называется распределением случайных величин (согласно СТБ ГОСТ Р 50779.10 распределение – это функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений).
Распределение случайной величины можно представить в табличном, графическом виде и при помощи статистических оценок.
При представлении распределения случайной величины в табличном виде каждому номеру исследуемой единицы продукции (номеру измерения) соответствует значение показателя качества для данной единицы продукции (результат измерения).
При представлении распределения случайной величины в графическом виде строят график распределения в координатах значение случайной величины – вероятность (частота, частость) значения случайной величины.
На рисунке ниже показаны графики распределения дискретной и непрерывной случайных величин.
|
|
|
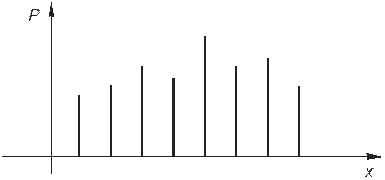
Рисунок - График распределения дискретной случайной величины
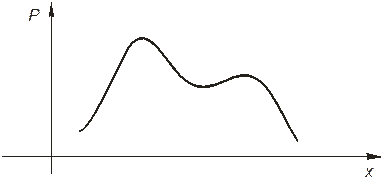
Рисунок - График распределения непрерывной случайной величины
Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате испытаний.
Следовательно, эмпирическим распределением случайной величины называется совокупность экспериментальных ее значений, расположенных в порядке возрастания, с указанием частот или частостей для каждого из значений (согласно СТБ ГОСТ Р 50779.10 распределение частот – это эмпирическое отношение между значениями признака и его частотами или его относительными частотами).
Таблица. Пример табличного представления теоретического распределения дискретной случайной величины
| X | X1 | X2 | X3 | X4 | X5 | |
| P(X) | P(X1) | P(X2) | P(X3) | P(X4) | P(X5) | SP(Xi)=1 |
Таблица. Пример табличного представления эмпирического распределения дискретной случайной величины
| X | X1 | X2 | X3 | X4 | X5 | |
| mx | 1/30 | 3/30 | 15/30 | 6/30 | 5/30 | Smxi=1 |
Графически эмпирическое распределение дискретной случайной величины можно представить в виде столбиковой диаграммы, образуемой набором столбцов равной ширины, высоты которых пропорциональны частотам дискретных значений случайной величины.
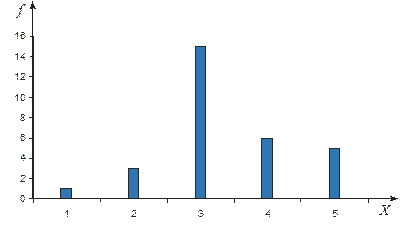
Рисунок - Столбиковая диаграмма дискретной случайной величины.
Если случайная величина является непрерывной, то возникают некоторые сложности с представлением ее распределения в виде таблицы или графика. Поэтому на практике при изучении случайных величин непрерывного типа полученные значения разбивают на равные интервалы с таким расчетом, чтобы значение интервала было несколько больше погрешности измерения исследуемой величины. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь следующий вид.
Таблица. Эмпирическое распределение случайной величины непрерывного типа.
| Интервал значений Х | Среднее арифметическое значение 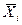
| Частота fi | Частость mi |
| 160,031 - 160,033 | 160,032 | 0,03 | |
| 160,033 - 160,035 | 160,034 | 0,03 | |
| 160,035 - 160,037 | 160,036 | 0,05 | |
| 160,037 - 160,039 | 160,038 | 0,26 | |
| 160,039 - 160,041 | 160,040 | 0,31 | |
| 160,041 - 160,043 | 160,042 | 0,19 | |
| 160,043 - 160,045 | 160,044 | 0,08 | |
| 160,045 - 160,047 | 160,046 | 0,05 | |
| Sfi = 100 | Smi = 1 |
Эмпирическое распределение случайной непрерывной величины графически может быть представлено в виде гистограммы распределения, полигона частот или полигона кумулятивных частот.
Гистограмма распределения представляет собой совокупность соприкасающихся прямоугольников, основания которых равны интервалам разбиения непрерывной случайной величины, а площади пропорциональны частотам, с которыми значения случайной величины попадают в эти интервалы (согласно СТБ ГОСТ Р 50779.10 гистограмма (распределения) – это графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов).
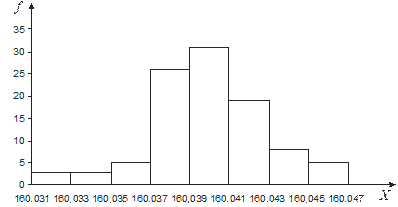
Рисунок - Гистограмма распределения случайной непрерывной величины.
Полигон частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны серединам интервалов разбиения, а ординаты – соответствующим частотам.
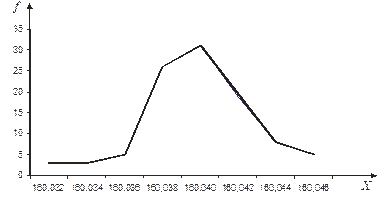
Рисунок - Полигон частот случайной непрерывной величины.
Полигон кумулятивныхчастот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам интервалов разбиения, а ординаты – либо кумулятивным частотам, либо кумулятивным частостям (кумулятивным относительным частотам).
|
|
|
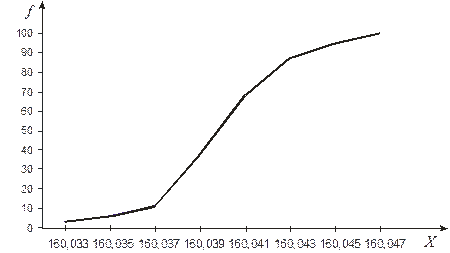
Рисунок - Полигон кумулятивных частот случайной непрерывной величины.
При теоретических описаниях случайных величин непрерывного типа используется функция распределения. Теоретическое распределение случайной непрерывной величины графически может быть представлено в виде интегральной, обратной интегральной, дифференциальной функций распределения и функции интенсивности.
Пусть Х — случайная величина, а х — какое-либо действительное число (при этом Х < х). Событию Х < х отвечает вероятность Р(Х < х), которая является функцией F(х), т.е.
Р(Х < х) = F(х)
F(Х) называется функцией распределениявероятностей случайной величины или интегральной функцией распределения.
Для дискретной случайной величины интегральная функция распределения F(Х) легко определяется по таблице или графику.
Таким образом, для приведенного выше примера распределения дискретной случайной величины (при Х < 4):
F(X) = Р(Х<4) = P(Х=1) + P(Х=2) + P(Х=3) = 1/30 + 4/30 +15/30 = 19/30
График интегральной функции распределения дискретной случайной величины будет иметь вид ступенчатой кривой. Ординаты кривой для любого значения Х будут представлять сумму вероятностей предшествующих значений.
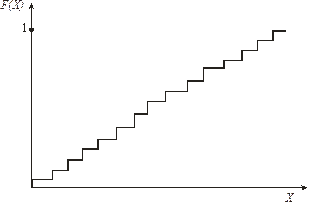
Рисунок - Интегральная функция распределения дискретной случайной величины
Вероятность того, что случайная величина при испытаниях окажется в границах двух заданных значений х1 и х2 (х2 > х1) равна приращению интегральной функции на этом участке, т.е.
Р(х1 ≤ Х ≤ х2) = Р(Х < х2) — Р(Х < х1) = F(Х2) — F(Х1)
Если обратиться к выше приведенному примеру распределения дискретной случайной величины, то при х1= 2 и х2 = 3:
Р(2≤Х≤3) = Р(Х < 3) — Р(Х < 2)= F(Х2) — F(Х1)= 4/30—1/30 = 3/30
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид монотонно возрастающей кривой. На практике с помощью интегральной функции распределения определяют теоретические частоты распределения.
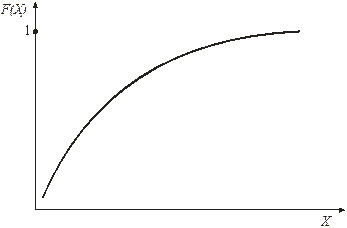
Рисунок - Интегральная функция распределения
непрерывной случайной величины
|
|
|
Обратная интегральная функция распределения равна разности между единицей и интегральной функции распределения.
Плотностью распределения (дифференциальной функцией распределения) случайной величины называют первую производную от интегральной функции распределения:
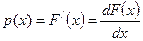
Для аналитического описания непрерывной случайной величины в теории надежности используют функцию интенсивности, равную отношению дифференциальной функции распределения к обратной интегральной функции распределения:
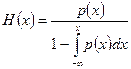
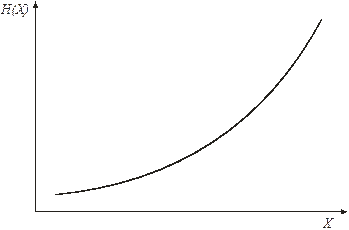
Рисунок - Функция интенсивности непрерывной случайной величины.
 2015-06-04
2015-06-04 3563
3563








