П.4. Подход различных авторов к формуле Шеннона

Интересно и поучительно проследить, как различные авторы подходили к знаменитой формуле Шеннона.

К. Шеннон (в 1940 г.) пишет ([46], с. 446):

«Если сигнал имеет мощность P, то сигнал, изменённый наложенной помехой, будет иметь мощность P + N. Число хорошо различимых значений есть

, (*)

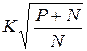где K – небольшая константа порядка единицы, зависящая от того, как истолковывается термин “хорошо различимый”».

Затем, при вычислении пропускной способности канала передачи двоичных цифр ([46], с. 448-449), коэффициент K «по умолчанию» приравнивается Шенноном к единице. Доказательство формулы (*) не очень убедительное, поскольку оно основано на теореме Котельникова-Шеннона, которая относится не к сигналам с ограниченной мощностью P, а к сигналам с ограниченной энергией: .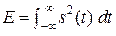

В 1949 г. В. Таллер в статье [57] рассмотрел передачу информации при наличии шума и пришёл к выводу ([57], с. 69):

«Пусть S будет среднее квадратичное значение наибольшего сигнала, который может быть получен в данной системе связи. Предположим, что близко к действительности, что изменение амплитуды сигнала, меньшее, чем амплитуда шума, не может быть обнаружено, но что изменение амплитуды [курсив Таллера – Г. Х.], равное шуму, уже обнаруживается.

Тогда, если N есть среднее квадратичное значение шума, смешанного с сигналом, то имеется 1 + S / N определяющих значений сигнала. Этим определяется s в выражении (1*)…». То есть H = k log s, где k – коэффициент пропорциональности ([57], с. 62), по поводу которого автор статьи ничего не говорит в её тексте; однако из аннотации к статье [57] следует, что k = 1.

В работе [10] 1948 г. Н. Винер, решая задачу оптимальной фильтрации стационарного случайного сигнала ξ(t) на фоне шума n (t) по критерию минимальной дисперсии отклонения выходного колебания оптимального стационарного линейного фильтра от сигнала на его входе (критерий Р. Фишера – [10], с. 153), для распределения по спектру максимального значения отношения «сигнал/шум» получает выражение Q (ω) = [ W _ξ(ω) + W_n (ω)]/ W_n (ω), где W _ξ(ω) и W_n (ω) – спектральные плотности мощности стационарного сигнала ξ(t) и шума n (t) соответственно.

А поскольку Винер, по совету Дж. фон Неймана, ввёл информационную меру количества информации, связанную с плотностью вероятности p (x), не по Фишеру, а соотношением + 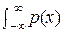log p (x) dx, то при гауссовских стационарных сигналах ξ(t) и помехах n (t) для скорости передачи информации он получает формулу (3.922), в которой нужно считать показатели степени не двойками, а единицами, и которая эквивалентна выражению:

C = .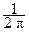

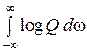Н. Винер добавляет ([10], с. 153):

«Именно этот результат и был получен автором [то есть Н. Винером – Г. Х.] и Шенноном …»

Если W _ξ(ω) = P, W_n (ω) = N, а канал передачи имеет верхнюю частоту среза W, то C = W log 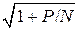, что действительно соответствует формуле Шеннона 1940 г.

В 1948 г. К. Шеннон ([46], с. 243-332) возвращается к формуле (*) уже «во-оружённый» понятиями энтропии дискретных и «непрерывных» сообщений (с. 308):

«Т е о р е м а 17. Пропускная способность канала с полосой частот W, в котором имеется белый тепловой шум мощности N, при условии, что средняя мощность передаваемых сигналов ограничена величиной P, равна

C = W log ».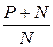

Поскольку максимальный темп передачи сигналов соответствует интервалу Найквиста Δ t = 1/(2 W ), это значит, что количество «чётко различимых уровней» есть .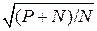

Гауссовские «непрерывные сигналы» и «помехи» соответствуют формуле Шеннона: H (Q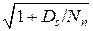) = log = log .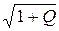

Доказательство теоремы 17, так же как и некоторых других, не очень убедительно. А. Н. Колмогоров по поводу доказательств Шенноном своих теорем заметил ([46], с. 14):

«При необычайном богатстве идей, данных в работах самого Шеннона, изложение в них обычно крайне туманно».