Оптимальные параметры для стратегии

ПЛАНИРОВАНИЯ НЕ ПОКРЫВАЕМОГО ДЕФИЦИТА

Избавляясь от q, S и t₁ в выражении для F (с учетом указанных выше равенств), после несложных преобразований (они опускаются из-за ограниченности объема работы) интересующая нас целевая функция F = F(Т,γ) как функция переменных Т и γ приводится к виду

F(Т, γ) = (1-g)×D × (Р_П – С_0П) – С₀ × 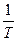– 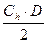∙Т× (1 –γ)² – 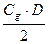×Т∙γ²–

– (C_П + P_П) ×D ∙Т× (1 – γ)² ×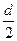

(*)

Обратим внимание на следующий граничный случай (вырожденный случай для стратегии управления, когда γ =1 и соответственно товар не поставляется). При γ → 1 значение F(Т, γ) в предельном случае будет отрицательным при любом Т >0 (если, по крайней мере, учитываются накладные расходы C₀ >0 и тем более, если учитываются издержки дефицита С_g >0). Поэтому в указанном граничном случае, если для параметра γ анализируется это граничное значение, то наилучшим решением будет:

q в случае C₀ >0 и С_g =0 (штрафные санкции дефицита отсутствуют) - Т → ∞,

т.е. товар не поставляется (при этом интенсивность потока доходов будет нулевой, а не отрицательной);

q в случае C₀ >0 и С_g >0 (штрафные санкции дефицита имеются) -

Т = ,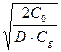

причем в этом случае оптимизируются именно процедуры выплаты издержек дефицита, а C₀ представляет соответствующие накладные расходы таких процедур, т.к. товар не поставляется (γ =1), причем интенсивность потока доходов будет, естественно, отрицательной.

Возвратимся к решению задачи оптимизации функции F = F(Т, γ), представленной выражением (*). Далее, меняя знак целевой функции на противоположный и умножая при этом для удобства записи на 2/ D, перепишем задачу оптимизации в виде

f(Т,g) ® min,

где функция f(Т,g) определяется равенством

f(Т,g) = 2 C₀ / Т × D + Т ×(1 – γ)²∙[ C_h + d(C_П+Р_П) ] +

+ Т × γ ²∙ С_g – 2 (1-g)×(Р_П – С_ОП).

Разумеется, при этом (из-за указанного выше «перехода» к противоположному знаку целевой функции) f(Т,g) уже характеризует соответствующие потери в интенсивности потока доходов при конкретном выборе интервала повторного заказа и параметра g, характеризующего «баланс» для промежутков времени дефицита и наличия запасов на таком интервале

Замечание. Легко видеть, что при Т→0 имеем f(Т,g)→∞ при любом 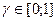. Кроме того, если Т→∞, то также f(Т,g)→∞ (кроме отмеченного выше граничного случая g=1, причем применительно к вырожденной ситуации, когда C_g = 0). Следовательно, при любом 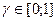интересующий нас минимум f(Т,g) как функции переменной Т существует. Кроме того, при любом фиксированном значении Т > 0 функция f(Т,g) (как функция переменной g ) представляет собой параболу, причем “ветвями вверх”. Следовательно, при любом значении Т > 0 минимум f(Т,g) как функции переменной g также существует. Таким образом, поставленная задача оптимизации будет иметь решение (естественно, при его нахождении требуется учитывать ограничение 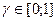, а также отдельно анализировать указанный выше граничный случай).