Закон розподілу ймовірностей
дискретної випадкової величини.
Закони біноміальний та Пуассона
Дискретною називають випадкову величину, можливі значення якої є окремі ізольовані числа (тобто між двома сусідніми можливими значеннями немає можливих значень), які ця величина приймає з певними ймовірностями. Іншими словами, можливі значення дискретної випадкової величини можна перенумерувати. Число можливих значень дискретної випадкової величини може бути скінченним або нескінченним (в останньому випадку множину всіх можливих значень називають зліченною).
Законом розподілу (рядом розподілу) дискретної випадкової величини називають перелік її можливих значень та відповідних їм ймовірностей. Закон розподілу дискретної випадкової величини  може бути заданий у вигляді таблиці, перший рядок якої містить можливі значення
може бути заданий у вигляді таблиці, перший рядок якої містить можливі значення 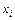 , а другий – імовірності
, а другий – імовірності 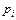 :
:
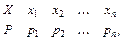
де 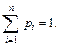
Закон розподілу дискретної випадкової величини  може бути також заданий аналітично (у вигляді формули):
може бути також заданий аналітично (у вигляді формули):
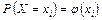
або за допомогою інтегральної функції.
Закон розподілу дискретної випадкової величини можна зобразити графічно, для чого в прямокутній системі координат будують точки 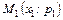 ,
, 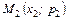 ,
, 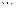 ,
, 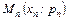 (
(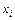 – можливі значення
– можливі значення  ,
, 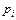 – відповідні ймовірності) та з'єднують їх відрізками прямих. Отриману фігуру називають багатокутником розподілу.
– відповідні ймовірності) та з'єднують їх відрізками прямих. Отриману фігуру називають багатокутником розподілу.
Біноміальним називають закон розподілу дискретної випадкової величини  – числа появ події в
– числа появ події в 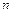 незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює
незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює 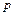 ; ймовірність можливого значення
; ймовірність можливого значення 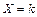 (числа
(числа 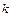 появ події) обчислюють за формулою Бернуллі:
появ події) обчислюють за формулою Бернуллі:
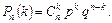
Якщо число випробувань велике, а ймовірність появи події 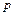 у кожному випробуванні дуже мала, то користуються наближеною формулою
у кожному випробуванні дуже мала, то користуються наближеною формулою
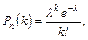
де 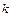 – число появ події в
– число появ події в 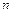 незалежних випробуваннях,
незалежних випробуваннях, 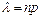 (середнє число появ події в
(середнє число появ події в 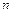 випробуваннях) і кажуть, що випадкова величина розподілена за законом Пуассона.
випробуваннях) і кажуть, що випадкова величина розподілена за законом Пуассона.
Числові характеристики
дискретних випадкових величин
Характеристикою середнього значення випадкової величини є математичне сподівання.
Математичним сподіванням дискретної випадкової величини називають суму добутків усіх її можливих значень на їх ймовірності:
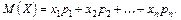
Якщо випадкова величина приймає зліченну множину можливих значень, то
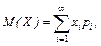
причому передбачається, що ряд, котрий знаходиться в правій частині рівності збігається абсолютно та сума всіх ймовірностей 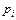 дорівнює одиниці.
дорівнює одиниці.
Математичне сподівання має наступні властивості.
В л а с т и в і с т ь 1. Математичне сподівання сталої величини дорівнює самій сталій:
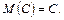
В л а с т и в і с т ь 2. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань доданків:
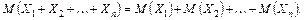
В л а с т и в і с т ь 3. Математичне сподівання добутку взаємно незалежних випадкових величин дорівнює добутку математичних сподівань співмножників:
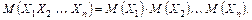
В л а с т и в і с т ь 4. Математичне сподівання біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи події в одному випробуванні:
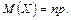
Характеристиками розсіяння можливих значень випадкової величини навколо математичного сподівання є, зокрема, дисперсія та середнє квадратичне відхилення.
Дисперсією випадкової величини  називають математичне сподівання квадрата відхилення:
називають математичне сподівання квадрата відхилення:
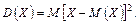
Дисперсію зручно обчислювати за формулою:
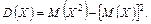
Дисперсія має наступні властивості.
В л а с т и в і с т ь 1. Дисперсія сталої дорівнює нулю:
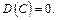
В л а с т и в і с т ь 2. Сталий множник можна виносити за знак дисперсії, попередньо піднісши його до квадрата:
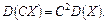
В л а с т и в і с т ь 3. Дисперсія суми незалежних випадкових величин дорівнює сумі дисперсій доданків:
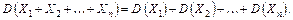
Дисперсія біноміального розподілу дорівнює добутку числа випробувань на ймовірності появи та непояви події в одному випробуванні
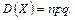
Середнім квадратичним відхиленням випадкової величини називають квадратний корінь із дисперсії:
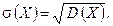
 2015-06-26
2015-06-26 979
979








