Если события А 1, А 2, …, Аn попарно несовместные, то вероятность суммы этих событий равна сумме их вероятностей, т. е.
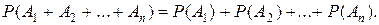
Пример 6.1. В урне 40 шариков: 15 голубых, 5 зеленых и 20 белых. Какова вероятность того, что из урны будет извлечен цветной шарик?
Извлечение цветного шарика означает появление либо голубого, либо зеленого шарика. Вероятность извлечения голубого шарика (событие А): Р (А) = 15/40 = 3/8. Вероятность извлечения зеленого шарика (событие В): Р (В) = 5/40 = 1/8. Так как события А и В несовместны, то Р (А + В) = Р (А) +
Р (В) =3/8 + 1/8 = ½.
Тот же результат получается и непосредственно по формуле 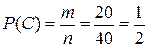 , где С – появление цветного шара; этому событию благоприятствует 20 элементарных исходов.
, где С – появление цветного шара; этому событию благоприятствует 20 элементарных исходов.
В общем случае
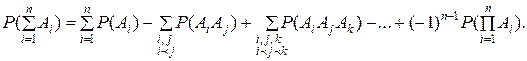
При n=2 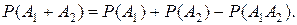
Таким образом, вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
При n =3 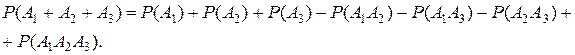
Сумма вероятностей событий A 1, A 2, …, An, образующих полную группу событий, равна единице:
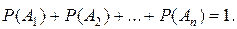
Сумма вероятностей противоположных событий равна единице:
|
|
|
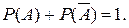
Пример 6.2. Вероятность того, что день будет дождливым, р =0,7. Найти вероятность того, что день будет ясным.
События – «день дождливый» и «день ясный» – противоположные, поэтому искомая вероятность q = 1 – 0,7 = 0,3.
Вероятность наступления события А при условии, что событие В уже произошло, называется условной и обозначается Р (А / В).
Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло, т. е.
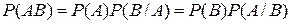 (теорема умножения вероятностей).
(теорема умножения вероятностей).
Если Р (А/В) = Р (А), то говорят, что событие А не зависит от события В. Свойство независимости событий взаимное – если Р (А / В) = Р (А), то и
Р (В /А) = Р (В).
Для независимых событий А и В теорема умножения вероятностей записывается так:
Р (АВ) = Р (А) Р (В).
Пример 6.3. Вероятность попадания в мишень для первого стрелка 0,85, а для второго – 0,8 Стрелки независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один стрелок.
Пусть события А, В, С – «попадание первого стрелка», «попадание второго», «попадание хотя бы одного» соответственно. Очевидно,
А + В = С, причем А и В совместны.
Тогда Р (С) = Р (А) + Р (В) – Р (АВ).
Так как А и В независимые события, то Р (АВ) = Р (А) Р (В). Тогда искомая вероятность
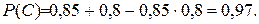
Пример 6.4. В урне 5 белых и 4 черных шара. Из нее вынимают подряд два шара. Найти вероятность того, что оба шара белые.
Путь А 1 – появление белого шара при первом вынимании, А 2 – появление белого шара при втором вынимании. Нас интересует событие А 1 А 2. По теореме умножения вероятностей
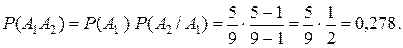
В случае трех событий А, В и С
|
|
|
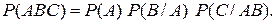
Если А, В и С – взаимно независимые события, то
Р (АВС) = Р (А) Р (В) Р (С).
Путь в результате опыта могут произойти независимые события А 1, А 2, …, Аm. Тогда вероятность того, что произойдет по крайней мере одно из этих событий, определяется по формуле
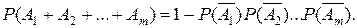
Пример 6.5. Вероятности попадания в цель при стрельбе из трех орудий таковы: 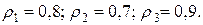 Найти вероятность хотя бы одного попадания (события А) при одном залпе из всех орудий.
Найти вероятность хотя бы одного попадания (события А) при одном залпе из всех орудий.
Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события Ai (попадание i- того орудия, i= 1, 2, 3) независимы в совокупности. Вероятности событий, противоположных событиям A 1, A 2, A 3 (т. е. вероятности промахов), соответственно равны
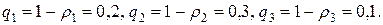
Искомая вероятность
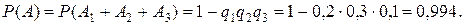
Если независимые события А 1, А 2, …, Аm имеют одинаковую вероятность, то вероятность появления хотя бы одного из этих событий выражается формулой
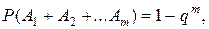 где q =1–
где q =1– 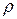 .
.
Пример 6.6. Имеется 4 станка. Для каждого из них вероятность того, что он работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы один станок.
События «станок работает» и «станок не работает» (в данный момент) – противоположные, поэтому сумма их вероятностей равна единице. Тогда вероятность того, что станок в данный момент не работал, равна
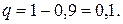 Искомая вероятность
Искомая вероятность 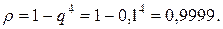
Пример 6.7. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Обозначим через А событие «при п выстрелах стрелок попадает в цель хотя бы один раз». События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому 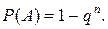 По условию
По условию 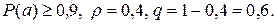 Тогда
Тогда 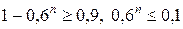 или
или 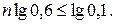 Окончательно
Окончательно 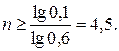
Итак, 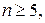 т. е. стрелок должен произвести не менее 5 выстрелов.
т. е. стрелок должен произвести не менее 5 выстрелов.
Вопросы для самопроверки
1. Чему равна вероятность суммы двух событий?
2. Чему равна вероятность суммы трех событий?
3. Чему равна вероятность суммы п несовместных событий?
4. Чему равна сумма вероятностей событий, образующих полную группу?
5. Чему равна сумма вероятностей противоположных событий?
6. Чему равна вероятность произведения двух событий?
7. Как определяется независимость двух событий?
8. Чему равна вероятность произведения двух независимых событий?
9. Чему равна вероятность появления хотя бы одного из m независимых событий, имеющих одинаковые вероятности?
 2015-06-24
2015-06-24 2732
2732
