Теорія графів бере свій початок з рішення видатним математиком Ейлером у 1736 р. задачі про кенігсбергські мости. Вона виникла в пруськом містечку Кенігсберг на річці Прегал. Жителі Кенігсберга полюбляли гуляти по доріжках, які включають сім мостів через річку. Людей цікавило питання, чи можуть вони, почавши шлях з однієї ділянки суши, обійти всі мости по черзі за одну ходу, і повернутися в початок шляху, не перепливаючи річку. План розташування семи мостів у Кенігсберзі наведений на рис. 6.32.

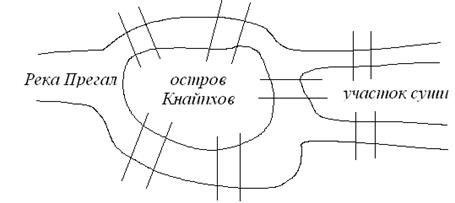
Рис. 6.32.
Ейлер замінив план міста графом (рис. 6.33), у якому ділянки суші зобразив як вершини, а мости, їх з'єднуючі – як ребра.
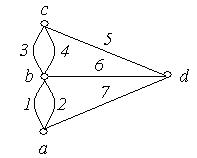
Рис. 6.33.
Для того, щоб відповістити на поставлене запитання, дамо ряд визначень.
Визначення 6.42. Ейлеровим циклом називається цикл, що містить всі ребра графа.
Ейлеров цикл можна вважати як слід олівця, що вичерчує граф, не відриваючись від паперу.
Відшукання ейлерових циклів пов'язане з рядом прикладних задач. Наприклад, при перевірці дорожньої мережі необхідно по кожній дорозі досліджуваної мережі проїхати тільки один раз і повернутися у вихідний пункт. Очевидно, що такі цикли існують не на будь-якому графі.
|
|
|
Визначення 6.43. Ейлеровим графом називається граф, що містить ейлеров цикл.
Теорема Ейлера. Кінцевий неорієнтований граф ейлеров тоді і тільки тоді, коли він зв'язний, і степінь всіх його вершин парна (при підрахунку степеня вершини, будь-яку інцидентну їй петлю вважати двічі).
Доведення:
Необхідність. Якщо граф  містить ейлеров цикл
містить ейлеров цикл 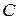 , то будь-які дві його вершини належать цьому циклу; граф зв'язний. Якщо при обході циклу
, то будь-які дві його вершини належать цьому циклу; граф зв'язний. Якщо при обході циклу 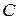 деяка вершина
деяка вершина 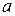 зустрічається
зустрічається 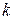 разів, то ми
разів, то ми 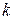 разів входимо і виходимо з неї (щораз по різних ребрах). Отже, степінь вершини
разів входимо і виходимо з неї (щораз по різних ребрах). Отже, степінь вершини 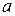 дорівнює
дорівнює 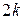 .
.
Достатність. Нехай граф  зв'язний і степінь будь-якої його вершини парна (рис. 6.34). Нехай
зв'язний і степінь будь-якої його вершини парна (рис. 6.34). Нехай 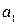 ‑ деяка вершина графа,
‑ деяка вершина графа, 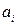 ‑ суміжна їй вершина. Цій вершині
‑ суміжна їй вершина. Цій вершині 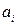 інцидентно хоча б одне ребро
інцидентно хоча б одне ребро 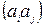 , відмінне від
, відмінне від 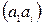 , вершині
, вершині 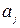 ‑ ребро, відмінне від
‑ ребро, відмінне від 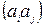 , і т.д.
, і т.д.
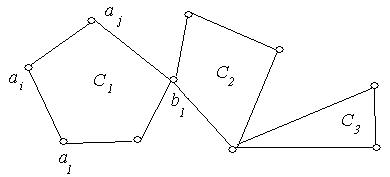
Рис. 6.34.
Побудуємо із цих ребер ланцюг, відзначаючи їх і не повторюючи вже пройдені. Граф  кінцевий, то цей ланцюг повинен закінчитися в деякій вершині
кінцевий, то цей ланцюг повинен закінчитися в деякій вершині 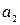 . Число ребер, інцидентных вершині
. Число ребер, інцидентных вершині 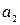 парне. Якби
парне. Якби 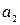 була відмінною від
була відмінною від 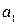 , ланцюг необхідно було би продовжити. Отже,
, ланцюг необхідно було би продовжити. Отже, 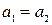 . Ми побудували цикл
. Ми побудували цикл 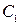 . Якщо в графі
. Якщо в графі  залишилися невідмічені ребра, то оскільки
залишилися невідмічені ребра, то оскільки  зв'язний, серед них найдеться хоча б одне, інцидентне якій-небудь вершині
зв'язний, серед них найдеться хоча б одне, інцидентне якій-небудь вершині 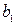 на циклі
на циклі 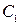 . Починаючи з вершини
. Починаючи з вершини 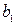 , ми можемо побудувати, як і раніше, цикл
, ми можемо побудувати, як і раніше, цикл 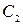 із ребер, що не ввійшли в
із ребер, що не ввійшли в 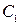 . З
. З 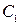 і
і 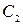 можна скласти новий цикл, що проходить із
можна скласти новий цикл, що проходить із 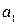 у
у 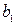 по
по 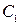 , потім уздовж усього циклу
, потім уздовж усього циклу 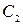 , і по частині циклу
, і по частині циклу 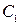 , що залишилася від
, що залишилася від 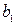 до
до 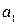 . Оскільки граф
. Оскільки граф  кінцевий, то після кінцевого числа кроків, ми одержимо ейлеров цикл.
кінцевий, то після кінцевого числа кроків, ми одержимо ейлеров цикл.
|
|
|
Отже, ми готові відповістити на запитання жителів Кенігсберга. Для цього підрахуємо степіні вершин графа, побудованого Ейлером (рис. 6.33): 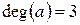 ;
; 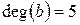 ;
; 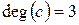 ;
; 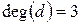 . Цей граф має непарні степені вершин. Отже, цей граф не має ейлерова цикла. Тобто, неможливо пройти кожен міст по черзі за одну ходу і повернутися у вихідну точку шляху.
. Цей граф має непарні степені вершин. Отже, цей граф не має ейлерова цикла. Тобто, неможливо пройти кожен міст по черзі за одну ходу і повернутися у вихідну точку шляху.
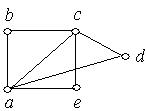
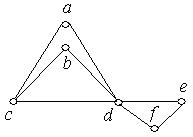
Приклад 6.22. Чи мають графи, зображені на рис. 6.35 (а, б), ейлеров цикл.
(а) (б)
Рис. 6.35.
Рішення:
Щоб відповістити на поставлене запитання, порахуємо степені вершин графа: а) 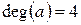 ;
; 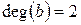 ;
; 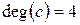 ;
; 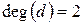 ;
; 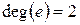 .
.
Степені всіх вершин графа, зображеного на рис. 6.35,а, парні, отже, граф, має ейлеров цикл;
б) 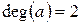 ;
; 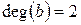 ;
; 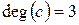 ;
; 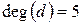 ;
; 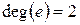 ;
; 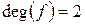 .
.
Степені вершин  і
і  графа, зображеного на рис. 6.35,б, непарні, отже, граф не має ейлеров цикл.
графа, зображеного на рис. 6.35,б, непарні, отже, граф не має ейлеров цикл.
Що стосується кенігсбергських мостів, можна задати інше питання: “ чи можливо пройти кожен міст по одному разі і не обов'язково повертатися у вихідну точку маршруту?” Відповідь на це питання жадає від нас знання наступного визначення і теореми.
Визначення 6.44. Шлях, що включає кожне ребро графа  тільки один раз, називається е йлеровим шляхом. У тому випадку, якщо ейлеров шлях не є ейлеровим циклом, він називається власним ейлеровим шляхом.
тільки один раз, називається е йлеровим шляхом. У тому випадку, якщо ейлеров шлях не є ейлеровим циклом, він називається власним ейлеровим шляхом.
Теорема 6.4. Граф  має власний ейлеров шлях тоді і тільки тоді, коли він зв'язний і рівно дві його вершини мають непарний степінь.
має власний ейлеров шлях тоді і тільки тоді, коли він зв'язний і рівно дві його вершини мають непарний степінь.
Тому що граф для задачі про кенігсбергські мости має чотири вершини з непарними степенями, то можна зробити висновок про те, що даний граф не має власного ейлерова шляху, а отже, неможливо пройти кожен міст по одному разі, навіть якщо не потрібно повертатися у вихідну точку маршруту.
Так, наприклад, граф, зображений на рис. 6.35,б, не має ейлерова циклу, але має власний ейлеров шлях, тому що дві його вершини мають непарний степінь.
Вправи:
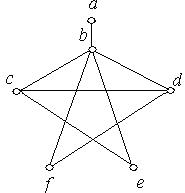
1. Серед наведених нижче графів знайти ті, які мають ейлеров цикл. Обґрунтувати відповідь.
а) б) в)
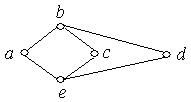
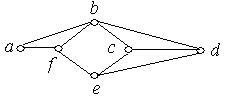
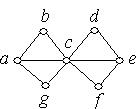
г) д) е)
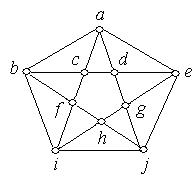
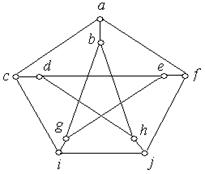
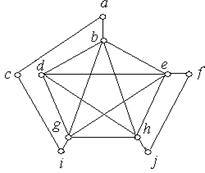
ж) з) і)
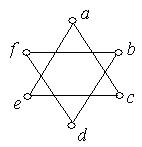
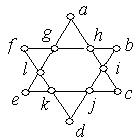
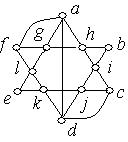
Рис. 6.36.
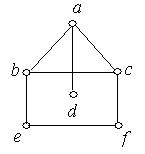
2. Серед наведених нижче графів знайти ті, які мають власний эйлеров шлях. Обґрунтувати відповідь.
а) б) в)
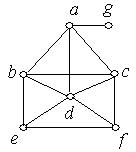
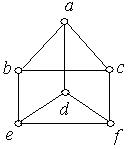
г) д) е)
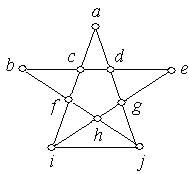
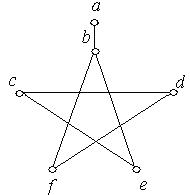
ж) з) і)
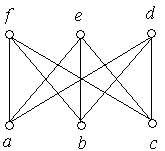
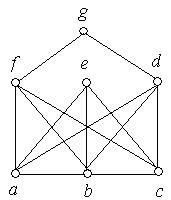
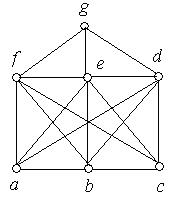
Рис. 6.37.
3. Придумати і побудувати графи, що містять ейлеров цикл. Обґрунтувати рішення.
4. Придумати і побудувати графи, що містять власний ейлеров шлях. Обґрунтувати рішення.
 2015-06-28
2015-06-28 1525
1525








