Рассмотрим два вектора 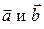 , обозначим буквой
, обозначим буквой 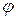 угол между ними. Скалярное произведение двух векторов
угол между ними. Скалярное произведение двух векторов 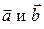 – это число, обозначаемое
– это число, обозначаемое 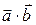 (точка может отсутствовать), или
(точка может отсутствовать), или 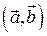 , и сопоставляемое указанной паре векторов по формуле
, и сопоставляемое указанной паре векторов по формуле 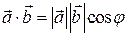 .
.
Скалярное умножение, очевидно, коммутативно: 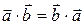 .
.
Непосредственно из определения вытекает, что
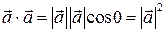
Будем обозначать скалярный квадрат 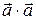 вектора
вектора 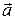 записью
записью 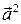 . Таким образом:
. Таким образом: 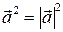 , и
, и 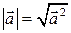 .
.
Также из определения скалярного произведения вытекает условие перпендикулярности: два вектора будут перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
Заметим, что если 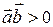 , то угол между векторами острый, если
, то угол между векторами острый, если 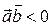 – угол тупой.
– угол тупой.
Косинус угла между векторами может быть выражен через скалярное произведение:
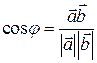
Определим проекции векторов друг на друга равенствами:
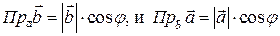
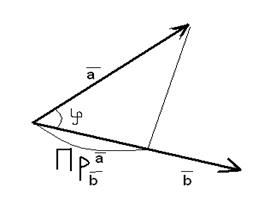
Теперь скалярное произведение может быть выражено через проекции, а именно:
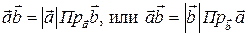 .
.
Также и проекции могут быть выражены через скалярное произведение:
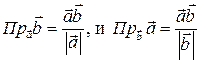
Нетрудно проверить свойства проекций:
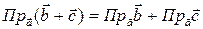 ,
,
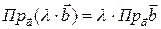 .
.
Эти свойства выполнены для любых векторов 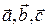 и для любого числа
и для любого числа 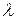 .
.
Из свойств проекций вытекают свойства скалярного произведения:
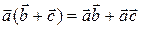 ,
,
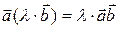
Докажем первое равенство: 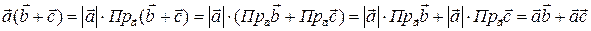 .
.
 2015-06-28
2015-06-28 459
459








