П. 14.2 Поверхности второго порядка

Если у поверхности вращения заменить 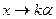, т.е. сжать все эти поверхности вдоль оси 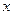, то получаются общие поверхности второго порядка. Исследовать их легко с помощью метода сечений (некоторые поверхности второго порядка не являются поверхностями вращения).

1. Эллипсоид: 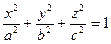, 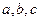– полуоси эллипсоида. Из 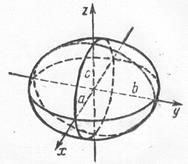уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида. Пересечём поверхность плоскостью 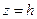, параллельной плоскости 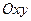. Тогда уравнение линии, полученной в сечении, имеет вид

.

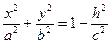Полагая 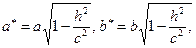получим уравнение эллипса 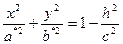с полуосям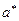и и .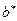

Аналогичная ситуация возникает при пересечении эллипсоида плоскостями, параллельными плоскостям 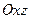и 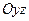. Заметим, что эллипсоид с равными полуосями: 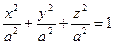называют сферой.

Из уравнения вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии эллипсоида.

2. Однополостной гиперболоид.

Из уравнения следует, что координатные плоскости являются плоскостями симметрии однополостного гиперболоида. Пересечение поверхности плоскостью 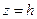есть эллипс: 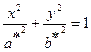, где 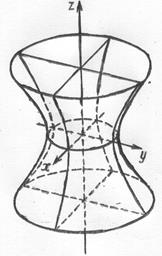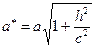, 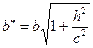. Сечения однополосного гиперболоида координатными плоскостям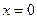и и 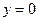представляют собой гиперболы, определяемые уравнениями соответственно

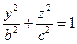и .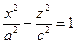

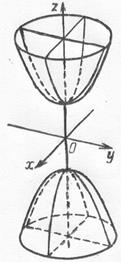
3. Двуполостной гиперболоид:

.

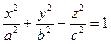Из уравнения видно, что координатные плоскости являются плоскостями симметрии, а начало координат центром симметрии двух полосного гиперболоида.

Сечение поверхности плоскостью 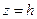(при 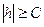) представляет собой эллипс 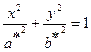с полуосями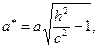 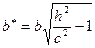. Сечения двуполостного гиперболоида плоскостям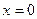и и 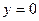представляют собой гиперболы

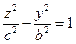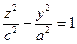и соответственно.

4. Эллиптический параболоид: .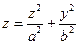

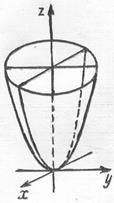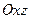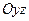Заметим, что координатные плоскости и являются плоскостями симметрии эллиптического параболоида. Ось 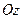называют осью данной поверхности. Сечение поверхности плоскостью 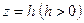, представляет собой эллипс 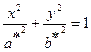, где .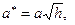

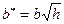Сечения эллиптического параболоида плоскостям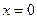и и 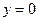являются параболам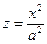и и .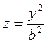

5. Конус: .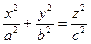

Отметим, что координатные плоскости являются плоскостями симметрии, я начало координат – центром симметрии конуса. Сечение 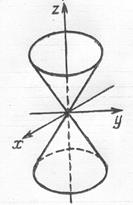конуса плоскостью 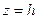представляет собой эллипс: 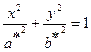с полуосям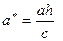и и .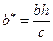

При пересечении конуса плоскостям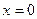и и 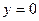получаются пары пересекающихся прямых

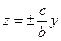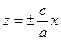и , соответственно, проходящих через начало координат.