Рассмотрим уравнение (4.1). Пусть 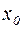 - некоторое приближение к его решению. Разложим левую часть уравнения по формуле Тейлора в точке
- некоторое приближение к его решению. Разложим левую часть уравнения по формуле Тейлора в точке 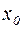
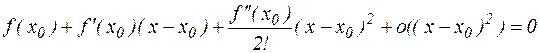 . (4.2)
. (4.2)
Метод Ньютона. Ограничимся в разложении (4.2) первыми двумя слагаемыми
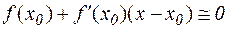
и разрешим полученное выражение относительно х
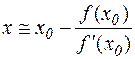 .
.
Последнее соотношение принимается в качестве базового для формирования вычислительного процесса. Он описывается формулой
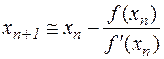
| (4.3) |
и называется методом Ньютона. Заметим, что правило (4.3) имеет вполне определённый геометрический смысл.
Действительно, рассмотрим уравнение касательной к графику функции 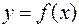 в точке
в точке 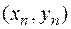
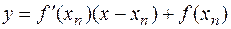
и определим её точку пересечения с осью ох. Имеем 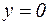 , откуда
, откуда
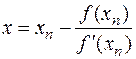 .
.
Из сравнения полученного выражения с (4.2) следует вывод, что
абсцисса точки пересечения касательной, проведённой к графику функции в точке 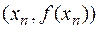 и представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.2). и представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.2).
|
 |
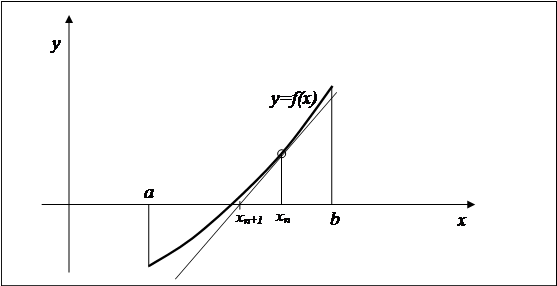
Рисунок 4.2. Метод Ньютона
По этой причине метод Ньютона называют ещё методом касательных.
|
|
|
Метод хорд. Рассмотрим (4.3). Заменим в нём
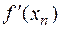 на
на 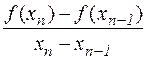 .
.
В результате этого получим новое вычислительное правило
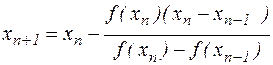
| (4.4) |
называемое методом хорд.
Выясним его геометрический смысл.
Рассмотрим точки кривой 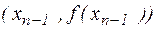 ,
, 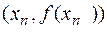 и проведем через них прямую
и проведем через них прямую
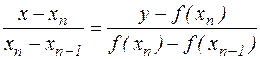 .
.
Найдем, далее, ее точку пересечения с осью абсцисс. Имеем
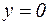 ,
, 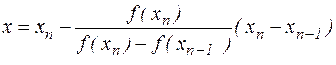 .
.
Сравнивая полученные выражения с соотношением (4.4), приходим к выводу, что
| абсцисса точки пересечения прямой, проходящей через точки кривой, определяемые двумя последними приближениями, представляет собой следующее приближение к решению уравнения (4.1) (Рисунок 4.3). |
 |
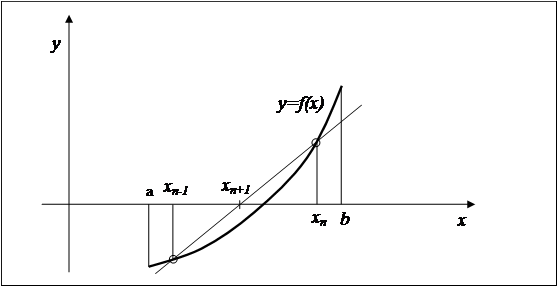
Рисунок 4.3. Метод хорд
 Сходимость, оценка погрешности. Рассмотрим эти вопросы на примере метода Ньютона.
Сходимость, оценка погрешности. Рассмотрим эти вопросы на примере метода Ньютона.
Рассмотрим отображение
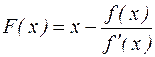 ,
,
где 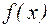 , - левая часть уравнения (4.1),
, - левая часть уравнения (4.1), 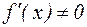 .
.
Заметим, что неподвижная точка отображения 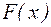 , если она есть, является и решением уравнения (4.1). Действительно, пусть существует значение х такое, что
, если она есть, является и решением уравнения (4.1). Действительно, пусть существует значение х такое, что 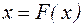 . Отсюда
. Отсюда
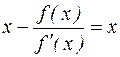 ,
,
откуда 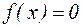 , что и требовалось.
, что и требовалось.
Далее, пусть 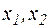 , - произвольные значения х, оценим величину
, - произвольные значения х, оценим величину 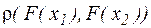 . Имеем
. Имеем
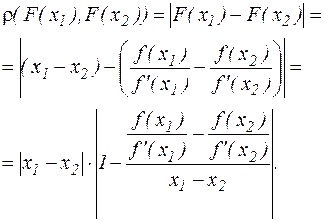
Тогда по теореме Лагранжа
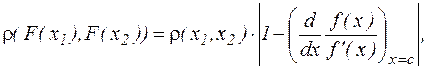
где 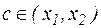 , или
, или
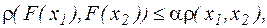
где 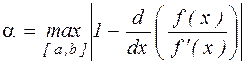 .
.
Отсюда следует утверждение.
Если 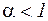 или, что то же или, что то же 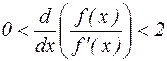 , то отображение , то отображение 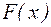 является сжимающим, последовательность (4.3), им формируемая,является сходящейся и, следовательно, метод касательных в этом случае сходится. является сжимающим, последовательность (4.3), им формируемая,является сходящейся и, следовательно, метод касательных в этом случае сходится.
|
Предельная точка х последовательности (4.3) является неподвижной точкой отображения 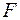 и является искомым решением. Погрешность
и является искомым решением. Погрешность 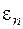 , - n -го приближения к решению, как и ранее, описывается соотношением (3.10).
, - n -го приближения к решению, как и ранее, описывается соотношением (3.10).
 2015-06-24
2015-06-24 316
316








