В данном параграфе главной целью является изучение основ теории групп. Группа – это множество, на котором задана некоторая бинарная (зависящая от двух аргументов) алгебраическая операция, удовлетворяющая определенным условиям. Понятие бинарной алгебраической операции лежит, следовательно, в основе всего задания теории групп.
Каждому ученику средней школы, известно слово «операция» и, одним из первых его значений, приходящих в голову, являются понятия арифметических операций – сложения, умножения, вычитания или деления. Операции можно производить не только над числами, но и над другими объектами: дизъюнкции и конъюнкции высказываний, композиции преобразований и т.д.
Во всех названых примерах операций мы имеем дело с некоторым множеством А (множество чисел, высказываний, преобразований и т.д.). При выполнении операции по двум элементам этого множества находят третий элемент того же множества (по двум заданным числам находят их сумму, по двум заданным высказываниям их конъюнкцию и т.д.). При этом ответ, зависит от порядка этих элементов (например, при вычитании чисел).
|
|
|
Дадим определение бинарной алгебраической операции.
Определение 1. 1. 1. Пусть А – непустое множество, тогда всякое отображение φ: A × A → A называют бинарной алгебраической операцией, заданной на множестве А.
Другими словами, бинарной операцией на А является правило или закон, согласно которому каждой упорядоченной паре элементов a и b из А ставится в соответствие однозначно определенный элемент d из A (φ: (a, b)→ d). Следуя арифметической традиции, результат применения бинарной операции φ к элементам a и b обозначают a φ b и называют композицией элементов a и b. В каждом конкретном случае композиция элементов получает свое название – сумма, произведение и т.п.
Определение 1.1.2. Множество А вместе с заданной на нем бинарной алгебраической операцией * называется группоидом и обозначается < A, *>.
Примеры: < R, +>, < R, *>, < R, - >.
Нетрудно заметить, что вычитание на множестве N не является бинарной операцией. Действительно, по определению бинарной алгебраической операции должно выполнятся условие: ( (а, b)
(а, b)  N 2) (
N 2) (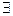 d
d  N 2) d = a – b. Составим отрицание:
N 2) d = a – b. Составим отрицание: 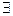 (а, b)
(а, b)  N 2 (
N 2 ( d є N) d ≠ a – b. При a = 2, b = 3 отрицание истинно, значит исходно утверждение – ложное. Следовательно, можно утверждать, что вычитание не является бинарной операцией на множестве N и < N, - > не является группоидом.
d є N) d ≠ a – b. При a = 2, b = 3 отрицание истинно, значит исходно утверждение – ложное. Следовательно, можно утверждать, что вычитание не является бинарной операцией на множестве N и < N, - > не является группоидом.
Таблица Кэли
На конечных множествах, содержащих не слишком много элементов, бинарную алгебраическую операцию удобно задавать с помощью таблицы, которая называется таблицей Кэли (А. Кэли (1821-1895) английский алгебраист). Эта таблица для группоида < A, *>, A = { a 1, a 2, …, an } заполняется следующим образом:
|
|
|
| * | a1 | a 2 | … | an |
| a 1 | a1 *a1 | a1 *a2 | … | a1 *an |
| a 2 | a2 *a1 | a2 *a2 | … | a2 *an |
| … | … | … | … | … |
| an | an *a1 | an | … | an *an |
Например, следующая таблица задает операцию * на множестве A = { a, b }:
| * | a | b |
| a | b | a |
| b | b | b |
Причем a * a = b * b= b* a= b и a* b= b. Поскольку результаты операции
принадлежат А, следовательно, < A, *> - группоид.
Свойства операций. Полугруппы
Известны свойства арифметических действий – переместительный (коммутативный) и сочетательный (ассоциативный) законы сложения и умножения действительных чисел. Сформулируем эти свойства для произвольной бинарной алгебраической операции. Поскольку мы рассматриваем, в определении группоида, операции на определенном множестве, то, чтобы не вводить дополнительных определений, и группоидом будем называть в соответствии с названием свойства операции.
Определение 1. 1. 3. Группоид < A, *> называется коммутативным (а сама операция коммутативной), если для любых двух элементов из A выполняется условие: ( a, b
a, b  А) а * b = b * а.
А) а * b = b * а.
Определение 1. 1. 4. Группоид < А, *> называется ассоциативным или полугруппой (а сама операция ассоциативной), если выполняется условие:
( а, b, с
а, b, с  А) а * (b * с) = (а* b) *с
А) а * (b * с) = (а* b) *с
Пусть < А,? > - полугруппа. Легко доказать следующие свойства.
1. (Обобщённый ассоциативный закон). Для любого конечного семейства элементов a 1 ,...,aк из А произведение a 1? a 2?...? aк не зависит от расстановки скобок, т. е. от последовательности умножений по два сомножителя.
2. Естественным образом вводится понятие степени с натуральным показателем: аn = a? a?...? a (n сомножителей а) для любых а  А и n
А и n  N, причём выполняются обычные свойства степеней:
N, причём выполняются обычные свойства степеней:
ak+n = ak? an и (ak) n = akn (k, n  N).
N).
3. Если полугруппа коммутативна, то имеет место обобщённый коммутативный закон: произведение любого конечного числа элементов из А не зависит от порядка сомножителей.
Можно сформулировать аналогичные свойства для полугруппы < А,+ >.
Моноид
Ещё из школы известны два правила: правило сложения любого числа с нулём и правило умножения любого числа на единицу. 0 и 1 - это нейтральные
элементы для операции сложения и умножения в R.
Определение 1. 1. 5. Элемент е  А группоида < А, * > называется нейтральным элементом, если для любого элемента a
А группоида < А, * > называется нейтральным элементом, если для любого элемента a  A a* e= e* a= a.
A a* e= e* a= a.
Теорема 1. 1. 1. Каждый группоид < А, * > содержит не более одного нейтрального элемента.
Доказательство. Предположим, что в группоиде А существуют два различных нейтральных элемента e 1 и е 2. Дважды воспользовавшись определением нейтрального элемента, получим: e 1 = е 1 ? e 2 = е 2 .
Поэтому, если в группоиде существует нейтральный элемент, то он единственный.
Чтобы установить, имеет ли группоид нейтральный элемент, надо выяснить, является ли группоид коммутативным, если да, то достаточно проверить одно условие: (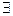 е
е  А) (
А) ( а
а  А) а * е = а. Если же нет, то надо проверять два условия: а * е = а и е * а = а.
А) а * е = а. Если же нет, то надо проверять два условия: а * е = а и е * а = а.
Пример. На множестве R операция * задана правилом: a * b = a + b – 1. Покажем, что < R, *> является группоидом, содержащим нейтральныйэлемент.
1. ( a, b
a, b 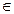 R) (
R) (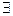 ! (а + b - 1)
! (а + b - 1)  R), следовательно, * - бинарная операция;
R), следовательно, * - бинарная операция;
2. ( a, b
a, b 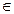 R) a * b = a+b -1= b * а в силу коммутативности сложения в R;
R) a * b = a+b -1= b * а в силу коммутативности сложения в R;
3. Условие 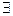 e
e  R
R  a
a  R a* е = а + е - 1= a выполняется при е - 1 = 0, т.к. нейтральным элементом на R относительно сложения является 0. Таким образом, е = 1 является нейтральным элементом относительно операции *.
R a* е = а + е - 1= a выполняется при е - 1 = 0, т.к. нейтральным элементом на R относительно сложения является 0. Таким образом, е = 1 является нейтральным элементом относительно операции *.
Определение 1. 1. 6. Полугруппа с нейтральным элементом называется моноидом.
Равенства а + (- а) = 0 и а? 1 = а напоминают нам о таких понятиях, как
противоположный и обратный элементы соответственно относительно операций сложения и умножения. Эти термины есть конкретизация такого математического понятия, как симметричный элемент. Правомерны следующие вопросы: каждый ли элемент множества имеет симметричный относительно операции в группоиде? При каких условиях элемент множества имеет симметричный?
|
|
|
Понятие симметричного элемента
Определение 1. 1. 7. Пусть группоид < А, * > имеет нейтральный элемент е, тогда элемент a  A называется симметризуемым, если для него существует а'
A называется симметризуемым, если для него существует а'  А такой, что а* а' = а' * а = е. Сам элемент а' называется в этом случае симметричным для а.
А такой, что а* а' = а' * а = е. Сам элемент а' называется в этом случае симметричным для а.
Теорема 1. 2. Если в полугруппе < А, * > элемент а симметризуем, то симметричный для него элемент а' единственный.
Доказательство. Допустим, что для а  А, существуют два симметричных элемента и и v. Тогда, учитывая, что дана полугруппа, получим:
А, существуют два симметричных элемента и и v. Тогда, учитывая, что дана полугруппа, получим:
и - и * е = u*(a*v) = (u* a)* v =e* v = v, т.е. и = v.
Исторически сложились и существуют два языка для выражения различных фактов, касающихся бинарных алгебраических операций: мультипликативный и аддитивный.
Формы записи бинарной операции
| Произвольная | Аддитивная | Мультипликативная |
| * а * b называется композицией a' -симметричный элемент для а е нейтральный элемент | + называется сложением а + b называется суммой -а -противоположный элемент для a нулевой элемент (нуль) | ? называется умножением а • b называется произведением а -1 - обратный элемент для а единичный элемент (единица) |
Далее в качестве основного языка выбран мультипликативный.
 2015-06-24
2015-06-24 17556
17556
