2015-06-24
549
| f | x1Ùx2 | x1Úx2 | x | x | ||
| f* | x1Úx2 | x1Ùx2 | x | x |
Теорема (Принцип двойственности).
Пусть F={f1,…,fm}. Положим F*={f*1,…,f*m}. Тогда, если формула Ф над базисом F реализует функцию f, то формула Ф* над базисом F*, полученная из формулы Ф заменой функций fi на двойственные функции f*i, реализует функцию f*.
Применительно к стандартному базису, двойственная к булевой формуле формула может быть получена из исходной заменой <Ú,Ù,0,1> → <Ù,Ú,1,0> соответственно с сохранением структуры формулы, т.е. с сохранением порядка действий.
Докажем частный случай теоремы (общий случай доказывается индукцией по глубине формулы). Пусть Ф(x1,…,xn) ≡ (F(y1,…,yn))(yi||fi),
тогда Ф*(x1,…,xn) ≡ (F*(y1,…,yn))(yi||fi*)
► Ф*(x1,…,xn) ≡ ((F(y1,…,yn))(yi||fi))* ≡ (F(f1(x1,…xn),…,fn(x1,…xn))* ≡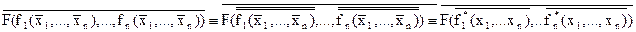 
≡ (F*(y1,…,yn))(yi||fi*) ◄
Следствием принципа двойственности является
Теорема. Любая булева функция, не равная тождественно 1, единственным образом представима в виде СКНФ:
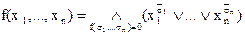
► f(x1,…,xn) ≡ f*(x1,…,xn)* ≡ (СДНФ(f*))*≡
≡ 
◄
|
|
|
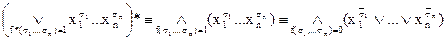Пример. Построим СКНФ для импликации. Имеем: x→y ≡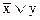 
Заметим, что способ задания функций совершенными формами в общем неэффективен: может потребоваться перечислить все конституенты. Хотя вот пример: х1Ú…Úх20 содержит 39 символов, а для задания её таблицей потребуется не менее миллиона строк.
Пример. Построение СДНФ и СКНФ мажоритарной функции.
Конституентами 1 являются наборы: Nf={011,101,110,111}. Получаем: К(011)=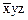 
, К(101)= 
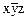, К(110)= 
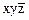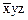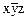, К(111)= xyz, т.ч. СДНФ= Ú Ú 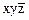Ú xyz.
Конституентами 0 являются наборы: {000,001,010,100}.
СКНФ =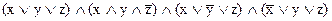 
Для проверки равенства форм надо раскрыть скобки. Сравнивая с ДНФ и КНФ мажоритарной функции, приведенными ранее, мы видим, что совершенные формы намного длиннее – как по числу конституент, так и по числу литералов.
