Формула метода ПГС имеет вид
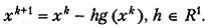 (5.12)
(5.12)
Соответствующая функция релаксации линейна (рис. 5.2):
R (λ) = 1 – λ h. (5.13)
Пусть собственные значения матрицы 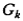 расположены в замкнутом интервале [ т, М ], причем М >> m > 0, так что
расположены в замкнутом интервале [ т, М ], причем М >> m > 0, так что 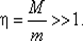 В этом случае условие (5.9), очевидно, выполняется, а неравенства (5.7) сводятся к требованию | R (λ i)| ≤ 1, i ∈ [1: n ], или
В этом случае условие (5.9), очевидно, выполняется, а неравенства (5.7) сводятся к требованию | R (λ i)| ≤ 1, i ∈ [1: n ], или
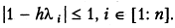 (5.14)
(5.14)
Эти оценки иллюстрируются рис. 5.2. Точка пересечения прямой R (λ) с осью абсцисс есть точка 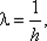 и чтобы при λ ∈ [ т, М ] зависимость R (λ) находилась в разрешенной области, необходимо выполнение неравенства
и чтобы при λ ∈ [ т, М ] зависимость R (λ) находилась в разрешенной области, необходимо выполнение неравенства 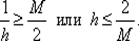 При этом ординаты функции релаксации характеризуют величину соответствующих множителей релаксации, которые в окрестности λ = т будут тем ближе к единице, чем больше величина
При этом ординаты функции релаксации характеризуют величину соответствующих множителей релаксации, которые в окрестности λ = т будут тем ближе к единице, чем больше величина 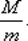 Будем считать, что для собственных чисел матрицы
Будем считать, что для собственных чисел матрицы 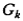 выполняются неравенства
выполняются неравенства
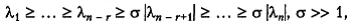
характерные для овражной ситуации. Тогда для точки 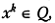 где Q — дно оврага, имеем, согласно (5.10),
где Q — дно оврага, имеем, согласно (5.10),
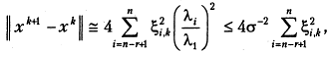
что может быть существенно меньше 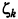 .
.
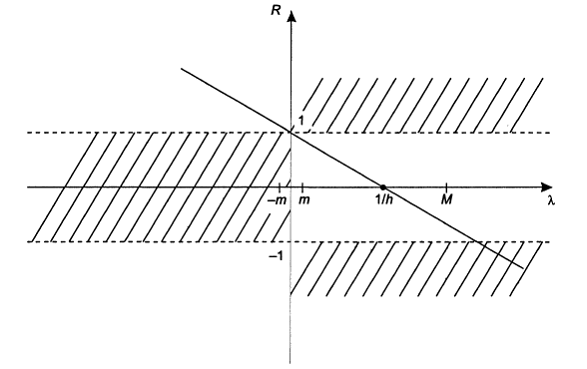
Рис. 5.2. Функция релаксации метода простого градиентного спуска
В результате соответствующие малым собственным значениям из окрестности λ = 0 слагаемые в (5.8) практически не будут убывать, а продвижение будет сильно замедленным. Это и определяет низкую эффективность метода (5.12).
В области λ < 0 функция (5.13) удовлетворяет условиям релаксации при любом значении параметра h. Практически параметр h в методе ПГС выбирается из условия монотонного убывания функционала на каждом шаге итерационного процесса. При отсутствии убывания величина h уменьшается до восстановления релаксационности процесса. Существуют различные стратегии выбора h, однако при больших η все эти методы, включая и метод наискорейшего спуска
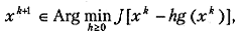
ведут себя приблизительно одинаково плохо даже при минимизации сильно выпуклых функционалов. Так же, как и в методе покоординатного спуска, здесь возможна ситуация заклинивания, представленная на рис. 5.3.
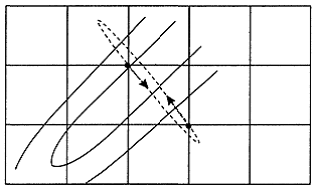
Рис. 5.3. Остановка метода ПГС в овражной ситуации
Метод ПГС представляет определенный интерес как средство оценки локальной степени овражности в окрестности точки замедления алгоритма. Выведем соответствующие соотношения.
Пусть замедление метода ПГС при минимизации некоторого функционала J (x) произошло в окрестности некоторой точки x 0. Тогда можно предположить, что достаточно длинный отрезок последовательности 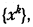 построенной из точки x 0, будет оставаться в области || х – x 0|| ≤ ζ0, и для J (x) справедлива квадратичная аппроксимация
построенной из точки x 0, будет оставаться в области || х – x 0|| ≤ ζ0, и для J (x) справедлива квадратичная аппроксимация
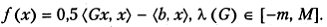 (5.15)
(5.15)
Метод (5.12) для (5.15) примет вид
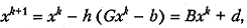 (5.16)
(5.16)
где 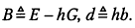
Записывая (5.16) для двух последовательных номеров 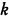 и вычитая полученные равенства, приходим к соотношению
и вычитая полученные равенства, приходим к соотношению
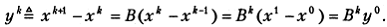 (5.17)
(5.17)
Согласно хорошо известному из курса численного анализа степенному методу определения максимального собственного числа симметричной матрицы, в результате проведения процесса (5.17) может быть получена оценка максимального собственного числа матрицы B:
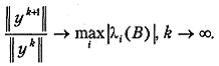 (5.18)
(5.18)
Полагая, что шаг h в итерационном процессе (5.16) выбирается из условия релаксационности (5.7), можно заключить, что 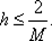 Построив график функции М релаксации 1 – h λ как функции от λ при фиксированном h, легко установить, что при
Построив график функции М релаксации 1 – h λ как функции от λ при фиксированном h, легко установить, что при 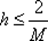 будем иметь
будем иметь
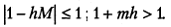
Таким образом,
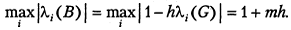
Следовательно, для достаточно больших 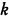 .
.
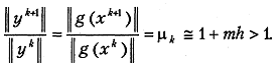 (5.19)
(5.19)
В результате приходим к требуемой оценке степени овражности функционала J (x) в окрестности точки x 0:
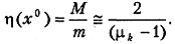
Практически поступают следующим образом. Проводят релаксационный процесс (5.16) до тех пор, пока он не замедлится и отношение 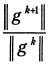 не стабилизируется около некоторого значения
не стабилизируется около некоторого значения  Далее используют полученную оценку степени овражности для выбора последующей стратегии оптимизации.
Далее используют полученную оценку степени овражности для выбора последующей стратегии оптимизации.
Рассуждая аналогично, для случая λ ∈ [ т, М ] из того же графика получим вместо (5.19) равенство 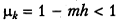 и соответствующую оценку
и соответствующую оценку 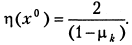 Легко геометрически видеть, что в этом случае для более устойчивого выделения в качестве максимального по модулю собственного числа матрицы В значения 1 – mh достаточно проводить процесс (5.16) с уменьшенным шагом h. Например, на практике удобно в любом случае осуществлять «лишнее» деление шага h на два после получения устойчивой релаксации.
Легко геометрически видеть, что в этом случае для более устойчивого выделения в качестве максимального по модулю собственного числа матрицы В значения 1 – mh достаточно проводить процесс (5.16) с уменьшенным шагом h. Например, на практике удобно в любом случае осуществлять «лишнее» деление шага h на два после получения устойчивой релаксации.
Общая оценка может быть записана в виде
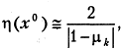
причем, сравнивая 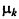 с единицей, можно установить характер выпуклости J (х) в окрестности точки x 0, что дает дополнительную полезную информацию.
с единицей, можно установить характер выпуклости J (х) в окрестности точки x 0, что дает дополнительную полезную информацию.
 2015-06-24
2015-06-24 582
582








