Практическое занятие №7

Наименование занятия: Кривые второго порядка.

Цель занятия: Научиться составлять кривых 2-го порядка, строить их.

Подготовка к занятию: Повторить теоретический материал по теме «Кривые 2-го порядка»

Литература:

1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
2. Дадаян А.А. «Математика», 2004г.

Задание на занятие:

1. Составить уравнение окружности с центром О(3; -2) и радиусом r = 5. Построить ее.
2. Построить окружность х² + у² + 6 х – 4 у – 3 = 0.
3. Составить каноническое уравнение эллипса, у которого малая ось 2b = 6, а расстояние между фокусами 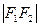= 8.
4. Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением 16 х ² + 25 у ² = 400.
5. Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот гиперболы, заданной уравнением 16 х ² – 25 у ² = 400.
6. Составить каноническое уравнение гиперболы, действительная ось которой 2b = 10, а уравнения асимптот имеют вид: .
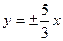7. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у ² = 8 х.
8. Составить уравнение параболы с вершиной в начале координат, если уравнение ее директрисы х + 3 = 0.

Порядок проведения занятия:

1. Получить допуск к работе
2. Выполнить задания
3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;
2. Выполненное задание;
3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Дать определение кривых второго порядка (окружности, эллипса, гиперболы, параболы), записать их канонические уравнения.
2. Что называется эксцентриситетом эллипса, гиперболы? Как его найти?
3. Записать уравнение равносторонней гиперболы

ПРИЛОЖЕНИЕ

Окружностью называется множество всех точек плоскости, равноудаленных от одной точки, называемой центром.

Пусть центром окружности является точка О (a; b), а расстояние до любой точки М (х;у) окружности равно R. Тогда (x – a)² + (y – b)² = R ² – каноническое уравнение окружности с центром О (a; b) и радиусом R.

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде: 2 x ² + 2 y ² – 8x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к каноническому виду. Для этого выделим полные квадраты:

x ² + y ² – 4 x + 2,5 y – 2 = 0

x ² – 4 x + 4 – 4 + y ² + 2,5 y + 25/16 – 25/16 – 2 = 0

(x – 2)² + (y + 5/4)² – 25/16 – 6 = 0

(x – 2)² + (y + 5/4)² = 121/16

Отсюда находим координаты центра О (2; -5/4); радиус R = 11/4.

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная, большая, чем расстояние между фокусами.

Фокусы обозначаются буквами F ₁, F ₂, расстояние между фокусами – 2 с, сумма расстояний от любой точки эллипса до фокусов – 2 а (2 а > 2 c), a – большая полуось; b – малая полуось.

Каноническое уравнение эллипса имеет вид: 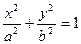, где a, b и c связаны между собой равенствами: a² – b² = c² (или b² – a² = c²).

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к длине большей оси и называется эксцентриситетом. 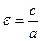или .

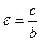Т.к. по определению 2 а > 2 c, то эксцентриситет всегда выражается правильной дробью, т.е. .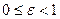

Пример. Составить уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: .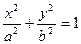

Расстояние между фокусами: 2 c = 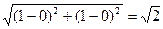, таким образом, a ² – b ² = c ² = 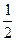. По условию 2 а = 2, следовательно, а = 1, b = 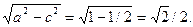Искомое уравнение эллипса примет вид: .

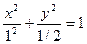Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Каноническое уравнение гиперболы имеет вид: 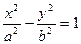или 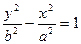, где a, b и c связаны между собой равенством a² + b² = c². Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Фокусы обозначаются буквами F ₁, F ₂, расстояние между фокусами – 2 с, разность расстояний от любой точки гиперболы до фокусов – 2 а (2 а < 2 c). Ось 2 а называется действительной осью гиперболы, ось 2 b – мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых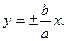

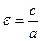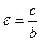Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси: или . Т.к. по определению 2 а < 2 c, то эксцентриситет гиперболы всегда выражается неправильной дробью, т.е. .

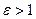Если длина действительной оси равна длине мнимой оси, т.е. а = b, ε = 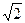, то гипербола называется равносторонней.

Пример. Составить каноническое уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением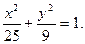

Находим фокусное расстояние c ² = 25 – 9 = 16.

Для гиперболы: c ² = a ² + b ² = 16, ε = c/a = 2; c = 2 a; c ² = 4 a ²; a ² = 4; b ² = 16 – 4 = 12.

Тогда 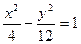- искомое уравнение гиперболы.

Параболой называется множество точек плоскости, равноудаленных от заданной точки, называемой фокусом, и данной прямой, называемой директрисой.

Фокус параболы обозначается буквой F, директриса – d, расстояние от фокуса до директрисы – р.

Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, имеет вид:

y ² = 2 px или y ² = -2 px

Уравнения директрис соответственно x = - p /2, x = p /2

Каноническое уравнение параболы, фокус которой расположен на оси ординат, имеет вид:

х ² = 2 pу или х ² = -2 pу

Уравнения директрис соответственно у = - p /2, у = p /2

Пример. На параболе у ² = 8 х найти точки, расстояние которой от директрисы равно 4.

Из уравнения параболы получаем, что р = 4. r = x + p /2 = 4; следовательно:

x = 2; y ² = 16; y = ±4. Искомые точки: M ₁(2; 4), M ₂(2; -4).