Градиентные методы решения задач

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Предположение о возможности описать зависимости меж­ду управ­ляемыми переменными с помощью линейных функций далёко не всегда адекватно природе моделируемого объекта. Попытки учесть нелинейные факторы приводят к формулировке более общих и сложных оптимиза­ционных за­дач. Изучение методов их решения составляет предмет научной области, получившей названия нелинейного программиро­вания.

Общая задача нелинейного программирования (ЗНП) оп­ределяется как за­дача нахождения максимума (или минимума) целевой функции f (x₁, х₂ ,..., х_п) на множестве D, определяемом системой ограничений равенств и неравенств:

gi (x₁, х₂ ,..., х_п)= 0, i=1: r,

f(x) ® max, D = { x Î R ⁿ, }(1)

gi (x₁, х₂ ,..., х_п)<= 0, i=r+ 1: m

где хотя бы одна из функций f или gi является нелинейной. По аналогии с линейным программированием ЗНП однознач­но определяется парой (D, f).

Как и в ЗЛП, вектор х* =(x₁*, x₂*,..., x_n*) Î D называется допус­тимым планом, а если для любого x Î D выполняется неравен­ство f(x*)>f(x), то х* называют оптимальным планом. В этом случае х* является точкой глобаль­ного максимума.

С точки зрения экономической интерпретации f(x) может рассмат­риваться как доход, который получает фирма (предпри­ятие) при плане выпуска х, a gi(x)<=0 как технологические ог­раничения на возможности выпуска продукции. В данном слу­чае они являются обобщением ресурсных ограничений в ЗЛП

Задача (1) является весьма общей. Набор ограничений, определяющих множество D, при необ­ходимости всегда можно свести либо к системе, состоящей из одних неравенств:

g(x) = 0 ó{ g(x)>=0; -g(x) <=0 }

либо, добавив фиктивные переменные у, к системе уравнений:

g(x)>=0 ó { g(x) – y² = 0 }.

Перечисленные свойства ЗНП существенно усложня­ют процесс их решения по сравнению с задачами линейного про­граммирования.

Градиентные методы решения задач

нелинейного программиро­вания.

Ведущее место среди прямых методов ре­шения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационар­ных точек дифференцируемой функции. Напомним, что стаци­онарной называется точка, в которой Ñ f(x) = 0 и которая в со­ответствии с необходимым условием оптимальности является «подозрительной» на наличие локального экстремума. Таким образом, применяя градиентный метод, находят множество точек локальных максимумов (или минимумов), среди которых определяется максимум (или минимум) глобальный.

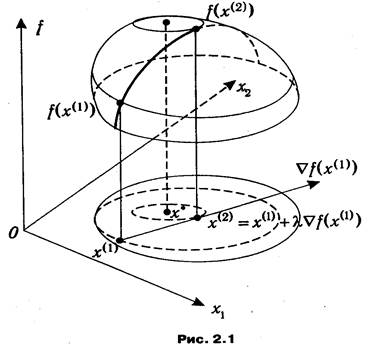
Пусть f(x)=f(x₁ , x₂ ,..., x_n) — дифференцируемая функ­ция, заданная на Rⁿ, а х^(q)=(х₁^(q), х₂^(q),..., х_n^(q)) – неко­торая текущая точка. Идея данного метода основана на том, что градиент функции указывает направление ее наиболее быстрого воз­рас­та­ния в окрестности той точки, в которой он вычислен. Поэтому, если из некоторой текущей точки х⁽¹⁾ переме­щаться в направлении вектора Ñ f(x⁽¹⁾), то функция f будет возрастать, по крайней мере, в некоторой окрестности х⁽¹⁾. Следовательно, для точки

x⁽²⁾ = x⁽¹⁾+ lÑ f(x⁽¹⁾), (l>0),

лежащей в такой окрестности, справедливо неравенство f(х⁽¹⁾)<=f(x⁽²⁾). Про­должая этот про­цесс, мы постепенно будем приближаться к точке некоторого локального максимума (см. рис. 2.1).

Однако как только определяется направление движения, сразу же встает вопрос о том, как далеко следует двигаться в этом направлении или, другими словами, возникает проблема выбора шага l в рекуррентной формуле

x^(q) = x^(q)+ lÑ f(x^(q)),

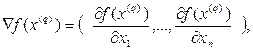
задающей последовательность точек, стремящихся к точке мак­симума. Как уже говори­лось выше, если x^(q) — нестационарная точка (т. е. |Ñ f(x^(q)) |>0), то при движении в направлении Ñ f(x^(q)) функция f(x) на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продол­жалось до тех пор, пока возрастание не прекратится.

Оговоримся, что каких-либо общих рекомендаций, каса­ющихся выбора исходной точки (или, как еще говорят, началь­ного приближения) x^{( 0 )} , не существует, однако по возможно­сти она должна находиться близко от искомого оптимального плана х*.

В зависимости от способа выбора шага l различают различные вари­анты гради­ентного метода.

Процедура «Поиск решения» в MS Excel содержит две разновидности гради­ентного метода – Метод Ньютона и метод спряженных гради­ентов.