Имеем функцию
F(x1, x2, x3)=a1x12 + a1x22 + a1x32 (4.18)
При этом х1+х2+х3=с; х1≥0, х2≥0, х3≥0. (4.19)
а1+а2+а3 – известные положительные величины.
Допустим, что С – ресурсы, которые надо распределить таким образом, чтобы функция (4.18) была минимальной. Иными словами, надо найти
Хi=fi(c, a1, a2, a3); i=1, 2, 3, чтобы F=Fмин.
Решение.
1. Введем дополнительные обозначения:
х1=с1; х1+х2=с2; х1+х2+х3=с3 (4.20)
2. Разделим ресурсы с на две части: х3 и с — х3 =с2
запишем так называемое рекуррентное соотношение:
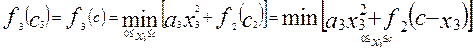 (4.21)
(4.21)
которое можно трактовать таким образом: найти такую функцию от С, которая в пределах 0 ≤ х3 ≤ С достигала бы минимума при выделении части х3 ресурсов для третьей составляющей функции F и части (с х3) ресурсов для оставшихся двух составляющих.
Примечание. В математике рекуррентной формулой называют формулу, выражающую каждый член последовательности через предыдущие члены. Здесь с2=сх3 сумма предыдущих членов.
3. Разделим оставшуюся после выделения х3 часть ресурса с2 = с—х3 на две части: х2 и (с2 х2).
|
|
|
Тогда функция, достигающая минимума в пределах 0≤х2≤с2 имеет выражение
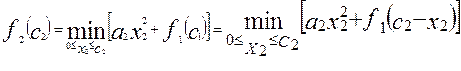 (4.22)
(4.22)
4. Оставшаяся часть ресурсов — это ресурсы, приходящиеся на первую составляющую:
f1(c1)=f1(x1)=f1(c2x2)=a1c12=a1(c2x2)2. (4.23)
теперь эти формулы - (4.21), (4.22), (4.23) - путем подстановок надо «пройти» дважды: снизу вверх (от конца к началу), подставляя последующие формулы в предыдущие, при этом находят условно оптимальные значения хi1, выраженные через сi, и сверху вниз (от начала к концу) — при этом определяются строго оптимальные значения хiопт=fi (с, а1, а2, а3).
5. Подставим (4.23) в (4.22) и найдем х2 =f2(с2, a1, а2), минимизирующее функциюf2 (с2). Имеем
f2(c2)=min [a2x22+a1(c2x2)2] (4.24)
0≤x2≤ C2
Берем производную от выражения в квадратных скобках и приравняем ее кнулю:
[a2x22+a1(c2+x2)2]' =2a2x22a1c2+2a1x2=0.
Тогда
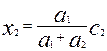 . (4.25)
. (4.25)
(Поскольку вторая производная, 2(а1+а2), положительна, значение (4.25) сообщает функции (4.24) минимум).
Подставляя (4.25) в (4.24), получаем
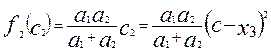 . (4.26)
. (4.26)
После подстановки (4.26) в (4.21) возьмем производную по х3 от выражения в квадратных скобках и. приравнивая ее к нулю, определим оптимальное (уже не условное) значение х3 опт:
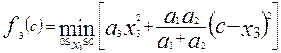 ;
;
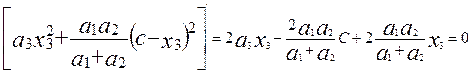 ;
;
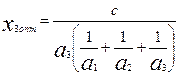 .
.
Подставим в (4.25) вместо С2 значение С2=СХ3 опт тогда
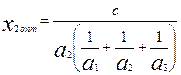 (4.27)
(4.27)
Наконец, определим, Х1 опт=С1=С2Х2 опт=СХ3 оптХ2 опт
 (4.28)
(4.28)
 2015-07-03
2015-07-03 339
339







