Отношение комплекса тока к комплексу напряжения пассивного двухполюсника называется комплексной проводимостью и обозначается 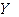 :
:
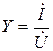 .
.
С комплексной проводимостью связаны следующие величины:
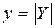 – полная проводимость,
– полная проводимость,
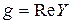 – активная проводимость,
– активная проводимость,
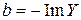 – реактивная проводимость,
– реактивная проводимость,
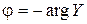 – аргумент комплексного сопротивления.
– аргумент комплексного сопротивления.
Согласно этим определениям, комплексную проводимость можно представить в виде
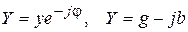 .
.
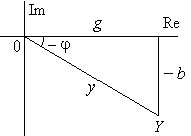 Рис. 13.6.
Рис. 13.6.
|
Из определения комплексной проводимости следуют равенства
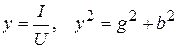 .
.
Комплексную проводимость изображают в виде “треугольника проводимостей” (рис. 13.6).
Реактивная проводимость, в отличие от активной, может быть отрицательной.
Отметим также, что 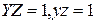 .
.
Пример: параллельное соединение резистора и конденсатора (рис. 13.7 - 13.9).
При параллельном соединении двухполюсников их токи складываются (вследствие 1-го закона Кирхгофа). Поэтому
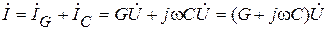 ,
,
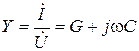 .
.
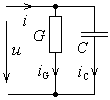 Рис. 13.7. Схема параллельного соединения G, С.
Рис. 13.7. Схема параллельного соединения G, С.
| 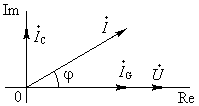 Рис. 13.8. Векторная диаграмма напряжения и
токов параллельного
соединения G, С.
Рис. 13.8. Векторная диаграмма напряжения и
токов параллельного
соединения G, С.
| 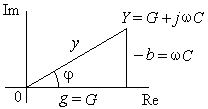 Рис. 13.9. Треугольник проводимостей параллельного соединения G, С.
Рис. 13.9. Треугольник проводимостей параллельного соединения G, С.
|
Из последней формулы видно, что комплексную проводимость параллельного соединения резистора и конденсатора можно получить сложением комплексных проводимостей резистора G и конденсатора j w С.
|
|
|
Ток двухполюсника 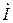 складывается из двух составляющих. Одна из них совпадает по фазе с напряжением и называется активной составляющей тока, а вторая сдвинута относительно напряжения на
складывается из двух составляющих. Одна из них совпадает по фазе с напряжением и называется активной составляющей тока, а вторая сдвинута относительно напряжения на 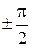 и называется реактивной составляющей тока. В нашем примере
и называется реактивной составляющей тока. В нашем примере 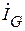 - активная, а
- активная, а 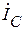 - реактивная составляющая тока.
- реактивная составляющая тока.
 2015-07-03
2015-07-03 3060
3060
