В линейном пространстве можно определить скалярное произведение векторов (х, у).
Свойства скалярного произведения:
1. (х, х) ³ 0, при этом (х, х) = 0 Û х = 0;
2. (х, у) = (у, х);
3. (х1+х2, у) = (х1, у) + (х2, у);
4. (λх, у) = λ (х, у).
Линейное пространство с определенным в нем скалярным произведением называется евклидовым пространством. В евклидовом пространстве норма вводится с помощью формулы
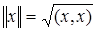 .
.
Из свойств скалярного произведения следует, что все аксиомы нормы при этом выполнены.
Наличие в линейном пространстве скалярного произведения позволяет ввести в этом пространстве не только норму (длину) вектора, но и угол между векторами. Угол между векторами х и у определяется формулой
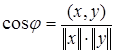 .
.
Если скалярное произведение (х, у) = 0, то вектора х и у называются ортогональными. Система ненулевых векторов называется ортогональной, если любые два из них ортогональны. Если вектора ортогональны, то они линейно независимы. Полная система ортогональных векторов образует в евклидовом пространстве ортогональный базис.
|
|
|
Рассмотрим некоторые примеры евклидовых пространств и ортогональных базисов в них.
1. Пространство R n с элементами 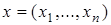 с обычными операциями сложения и умножения и скалярным произведением
с обычными операциями сложения и умножения и скалярным произведением
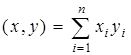
представляет собой хорошо известный пример евклидова пространства. Один из возможных ортогональных базисов в нем образуют векторы
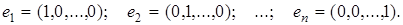
2. Пусть f ÎC[ a; b ] – пространство непрерывных функций. Оно удовлетворяет аксиомам линейного пространства, поэтому функции можно рассматривать как векторы. Определим в этом пространстве скалярное произведение. Положим
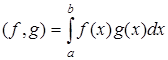 .
.
Нетрудно проверить, что введенное таким образом скалярное произведение удовлетворяет всем требуемым свойствам. Квадратичная метрика, рассмотренная в примере 7 пункта 1, индуцируется нормой, порождаемой этим скалярным произведением
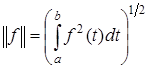 .
.
Рассмотрим системы функций, образующих ортогональный базис в пространстве С[ a, b ]. Среди различных ортогональных базисов важнейшим является тригонометрическая система, состоящая из функций
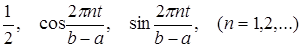
В качестве другого ортогонального базиса можно взять многочлены Лежандра:
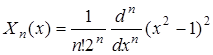 .
.
Все рассмотренные примеры играют важную роль в дальнейшем изложении.
 2015-07-21
2015-07-21 471
471







