2015-07-21
354
Пусть заданы три конечных непустых упорядоченных множества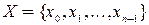 
, 
, 
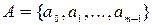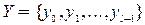, которые называются соответственно входным алфавитом, алфавитом состояний, выходным алфавитом.
Определение: Детерминированным конечным автоматом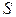 
называется объект 
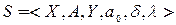, который в дискретные моменты времени (такты) 
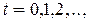может принимать состояния из алфавита 
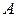(в момент времени 
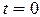он находится в начальном состоянии 
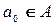), причем в каждом такте 
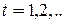. на него воздействует какой-либо символ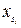 
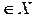, и он переходит из предыдущего состояния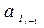 
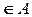, определяемого функцией перехода 
= 
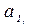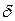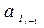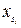(, ) и выдает выходной символ 
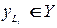, определяемый функцией выходов 
.
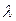Автомат, находящийся в момент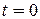 
в состоянии 
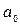, называется инициальным. В зависимости от способа задания функции 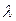различают конечные автоматы следующих видов:
1. 
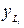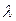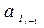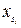= (, ) - автомат 1-го рода (Мили)
2. 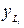= 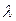(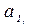, 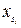) - автомат 2-го рода
3. = (, 
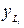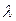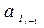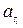) - правильные автоматы
4. 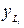= 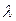(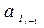) - правильные автоматы 1-го рода
5. 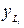= 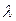(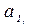) - правильные автоматы 2-го рода (Мура)
6. 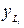= 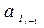- абстрактные автоматы 1-го рода
7. 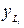= 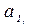- абстрактные автоматы 2-го рода
8. 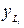= 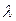(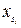) - автоматы без памяти (комбинационные схемы).
|
|
|
Если функци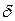и и 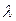определены всюду на множествах совокупностей значений своих аргументов, то конечный автомат 
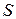называется вполне определенным. В противном случае автомат называется частичным.
