Дифференцируемость функции

Опр. Числовая функция y=f(x) называется дифференцируемой в точке 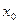, если ее приращение в этой точке можно представить в виде:

,

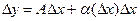где А – некоторое число, 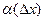- функция от 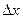, являющаяся бесконечно малой при .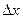

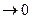Утв. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Теорема1 (о связи между непрерывностью и дифференцируемостью).

Если функция дифференцируема в точке, то она непрерывна в этой точке.

Док-во. Пусть функция y=f(x) дифференцируема в точке 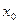. Тогда, по определению, ее приращение можно представить в виде 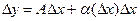. Переходя в этом равенстве к пределу при 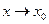, получим:

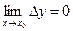, что соответствует определению непрерывности функции.▲

Теорема 1 является необходимым (но не достаточным) признаком дифференцируемости функции в точке. Обратная теорема, вообще говоря, не верна, т.е. если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.

Пример.

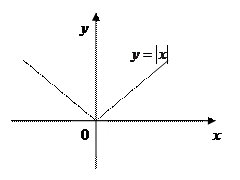Рассмотрим функцию 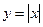, непрерывную в нуле. Докажем, что функция не дифференцируема в т. х=0.

;

.

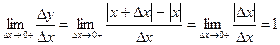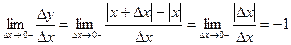Т.к. односторонние пределы в нуле не равны, предел 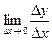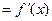не существует.