17.5.1. У лінейнага аператара prx лінейнай прасторы V2 вектар 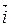 з’яўляецца ўласным з уласным значэннем 1, паколькі
з’яўляецца ўласным з уласным значэннем 1, паколькі 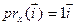 .
.
Так як  , вектар
, вектар 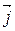 - уласны, якому адпавядае ўласнае значэнне 0.
- уласны, якому адпавядае ўласнае значэнне 0.
17.5.2. Вектар 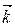 з’яўляецца ўласным вектарам аператара паварота прасторы V3 вакол восі Oz, якому адпавядае уласнае значэнне 1.
з’яўляецца ўласным вектарам аператара паварота прасторы V3 вакол восі Oz, якому адпавядае уласнае значэнне 1.
17.5.3. Ненулявыя паліномы нулявой ступені і толькі яны з’яўляюцца уласнымі вектарамі аператара дыферанцавання D прасторы P [x]. Ім адпавядае ўласнае значэнне 0.
Ул-ць 17.6. Калі 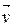 - уласны вектар лінейнага аператара f ÎEnd(V), якому адпавядае ўласнае значэнне
- уласны вектар лінейнага аператара f ÎEnd(V), якому адпавядае ўласнае значэнне 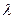 ÎP, тады для адвольнага
ÎP, тады для адвольнага 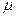 ÎP\{0} вектар
ÎP\{0} вектар 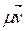 таксама з’яўляецца ўласным вектарам аператара f, якому таксама адпавядае ўласнае значэнне
таксама з’яўляецца ўласным вектарам аператара f, якому таксама адпавядае ўласнае значэнне 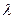 .
.
Доказ. Па ўмове 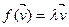 . Тады відавочна, што
. Тады відавочна, што 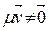 і
і 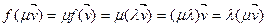 .■
.■
Вынік 17.7 Калі 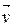 - уласны вектар лінейнага аператара f ÎEnd(V), якому адпавядае уласнае значэнне
- уласны вектар лінейнага аператара f ÎEnd(V), якому адпавядае уласнае значэнне 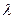 , тады падпрастора P
, тады падпрастора P 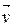 ={
={ 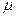
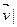
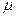 ÎP} з’яўляецца f -інварыянтнай і кожны ненулявы вектар гэтай прасторы з’яўляецца ўласным вектарам гэтай прасторы з’яўляецца ўласным вектарам f, якому адпавядае ўласнае значэнне
ÎP} з’яўляецца f -інварыянтнай і кожны ненулявы вектар гэтай прасторы з’яўляецца ўласным вектарам гэтай прасторы з’яўляецца ўласным вектарам f, якому адпавядае ўласнае значэнне 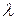 .
.
|
|
|
Доказ. Вынікае з 17.6 і таго, што f 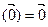 .■
.■
Азн. 17.8 Няхай 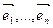 (3) - базіс прасторы V, f ÎEnd(V) і А =
(3) - базіс прасторы V, f ÎEnd(V) і А = 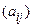 -матрыца аператара f у базісе (3). Характэрыстычным паліномам матрыцы А, а таксама характэрыстычным паліномам f называецца паліном
-матрыца аператара f у базісе (3). Характэрыстычным паліномам матрыцы А, а таксама характэрыстычным паліномам f называецца паліном
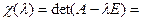
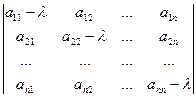 (4)
(4)
Карэктнасць гэтага азначэння вынікае з 17.9.
Ул-ць 17.9 Характэрыстычны паліном лінейнага аператара залежыць ад таго, у яім базісе знаходзіцца яго матрыца.
Доказ. Няхай 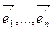 (5)
(5)
таксама базіс прасторы V, f мае ў гэтым базісе матрыцу А’. Калі Т – матрыца пераходу ад базіса (3) да базіса (5), тады па тэарэме 11.8, А’ = Т-1АТ. Адсюль атрымоўваем, што
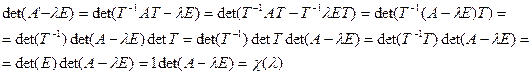 .■
.■
Тэарэма 17.10. Элемент 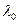 ÎP з’яўляецца ўласным значэннем аператара f тады і толькі тады, калі ён з’яўляецца коранем характэрыстычнага палінома
ÎP з’яўляецца ўласным значэннем аператара f тады і толькі тады, калі ён з’яўляецца коранем характэрыстычнага палінома 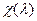 лінейнага аператара f.
лінейнага аператара f.
Доказ. Няхай 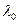 ÎP - уласнае значэнне лінейнага аператара f, якое адпавядае уласнаму вектару
ÎP - уласнае значэнне лінейнага аператара f, якое адпавядае уласнаму вектару 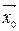 і мае ў базісе (3) ненулявы слупок каардынат X0, а f мае у (3) матрыцу А.
і мае ў базісе (3) ненулявы слупок каардынат X0, а f мае у (3) матрыцу А.
Тады паколькі 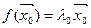 , значыцца AX0 =
, значыцца AX0 = 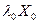 , адкуль вынікае, што AX 0=
, адкуль вынікае, што AX 0= 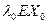 і
і 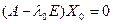 . (6)
. (6)
Разгледзім аднародную сістэму n лінейных раўнанняў адносна n невядомых – кампанент слупка X. З гэтага вынікае, што дэтэрмінант матрыцы каэфіцэнтаў сістэмы – выражэння: 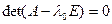 , значыцца
, значыцца 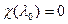 .
.
Няхай 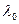 - корань характэрыстычнага палінома
- корань характэрыстычнага палінома 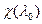 лінейнага аператара f. Фіксуем у V базис (3). Разгледзім аднародную сістэму (7). Дэтэрмінант матрыцы каэфіцэнтаў сістэмы (7) роўны
лінейнага аператара f. Фіксуем у V базис (3). Разгледзім аднародную сістэму (7). Дэтэрмінант матрыцы каэфіцэнтаў сістэмы (7) роўны 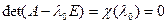 , значыцца ранг матрыцы каэфіцэнтаў меньшы за колькасць невядомых. Паколькі сістэма аднародная, значыцца ранг пашыранай матрыцы сістэмы роўны рангу рангу матрыцы каэфіцыентаў і меньшы за колькасць невядомых, значыцца сістэма (7) мае бясконцае мноства рашэнняў. Няхай X0 – ненулявы слупок яе рашэнняў. Маем, што
, значыцца ранг матрыцы каэфіцэнтаў меньшы за колькасць невядомых. Паколькі сістэма аднародная, значыцца ранг пашыранай матрыцы сістэмы роўны рангу рангу матрыцы каэфіцыентаў і меньшы за колькасць невядомых, значыцца сістэма (7) мае бясконцае мноства рашэнняў. Няхай X0 – ненулявы слупок яе рашэнняў. Маем, што 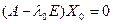 і AX0 =
і AX0 = 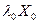 .
.
|
|
|
Разгледзім вектар 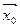 , які ў базісе (3) мае слупок каардынат X0. Так як слупок X0 ненулявы,
, які ў базісе (3) мае слупок каардынат X0. Так як слупок X0 ненулявы, 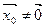 . З (8), згодна з тэарэмай 11.5 і ўласцівасці 5.11, (8) эквівалентна таму, што
. З (8), згодна з тэарэмай 11.5 і ўласцівасці 5.11, (8) эквівалентна таму, што 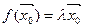 , значыцца,
, значыцца, 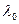 - уласнае значэнне f, якое адпавядае ўласнаму вектару
- уласнае значэнне f, якое адпавядае ўласнаму вектару 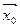 .■
.■
 2015-07-14
2015-07-14 250
250








