Разложение функций в степенной ряд

Определение 1. Говорят, что функция f (x) м о ж е т б ы т ь р а з л о ж е н а в с т е п е н н о й р я д на интервале (- R, R) в предположении, что интервал не вырождается в точку, т.е. R > 0, если существует степенной ряд, сходящийся к функции f (x) на этом интервале.

Если функция f (x) может быть разложена в степенной ряд на интервале (- R, R), то она называется а н а л и т и ч е с к о й функцией переменной х на этом интервале.

Предположим, что f (x) может быть разложена наинтервале (- R, R), R > 0,в степенной ряд f (x) = а_о + а₁х + а₂х² + …+ а_nxⁿ +…, где коэффициенты а_о, а₁, а₂, …, а_n,… - неизвестны.

Утверждение 1 (необходимое условие разложения). Если функция f (x) может быть разложена в степенной ряд на интервале (- R, R), то эта функция имеет на указанном интервале непрерывные производные любого порядка.

Д о к а з а т е л ь с т в о. (см. [1, с.107]).

Степенной ряд можно почленно дифференцировать внутри (– R, R).

Все ряды, полученные таким образом сходятся.

Тогда суммы представляют собой функции, непрерывные внутри указанного промежутка сходимости. Значит существуют производные любого порядка, непрерывные на (– R, R).

Утверждение 2 (единственность разложения). Если функция f (x) может быть разложена в степенной ряд на интервале (- R, R), то лишь единственным образом.

Д о к а з а т е л ь с т в о. (см. [1, с.107]).

Степенной ряд можно почленно дифференцировать внутри (– R, R).

f¢ (x) = а₁ + 2 а₂х + …+ nа_nx^n-1 +…

f¢¢ (x) = 2 а₂ + …+ n (n- 1) а_nx^n-2 +…

Пусть

х = 0, тогда f (0) = а_о, f¢ (0) = а₁, …, f ^{( n )}(0) = n! а_n

То есть коэффициенты однозначно определяются формулой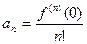

Предположим, что функция f (x) имеет на интервале (- R, R) непрерывные производные любого порядка.

Определение 2. Р я д о м Т е й л о р а функцииf (x) в окрестности точки х_о называется степенной ряд вида

=

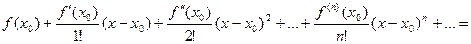
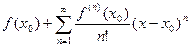
независимо от того сходится этот ряд или нет и чему равна его сумма.

Числа 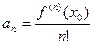, n Î N называются коэффициентами Тейлора функции f (x) в точке х _о.

Р я д М а к л ó р е н а

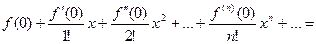
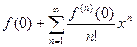
получен из ряда Тейлора при х _о= 0.

Утверждение 3. Если функция f (x) может быть разложена в степенной ряд на интервале (- R, R), то этот ряд является рядом Тейлора функции f (x).

Д о к а з а т е л ь с т в о.

Очевидно из утверждения 2.

Обратно.

Пусть функция f (x) бесконечно дифференцируема в окрестности точки х _о.

Составим формально ряд: .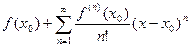

Г О В О Р Я Т, что функция f (x) п о р о ж д а е т ряд Тейлора и п и ш у т f (x) ~ .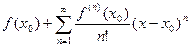

Ряд, порожденный функцией f (x):

1) может сходиться к функции f (x), т.е. S (x) = f (x).

2) может сходиться к другой функции S (x) ¹ f (x).

3) может расходиться.

Пример.

Для произвольной функции f (x) сумма её ряда Тейлора не обязательно совпадает с самой функцией.

Рассмотрим функцию

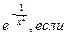х ¹0;

f (x) =

0, если х =0.

Функция f (x) непрерывна на (- ∞,∞).

Функция f (x) бесконечно дифференцируема на (- ∞,∞).

f (0) = f¢ (0) = … = f ^{( n )}(0) = … = 0.

f (x) ~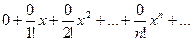

Ряд сходится. Его сумма S (x) = 0 ¹ f (x).

Утверждение 4 (необходимое и достаточное условие разложенияфункции в ряд Тейлора). Для того чтобы функция f (x) была разложимой в ряд Тейлора в некоторой окрестности точки х ₀ , необходимо и достаточно, чтобы в этой окрестности функция f (x) была бесконечно дифференцируемой и остаточный член в формуле Тейлора стремился к нулю при n ® ¥.

Д о к а з а т е л ь с т в о.

Утверждение 5 (достаточное условие разложения). Если в некоторой окрестности точки х ₀ все производные функции f (x) равномерно ограничены в совокупности, то функция f (x) является в этой окрестности суммой своего ряда Тейлора.

Д о к а з а т е л ь с т в о.