Методы функциональной интерполяции
Пусть на множестве 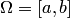 задана сетка
задана сетка 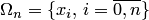 , определяемая
, определяемая 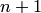 точкой
точкой 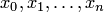 , а на сетке задана сеточная функция
, а на сетке задана сеточная функция 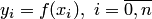
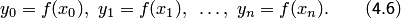
В некоторых случаях 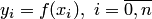 является сеточным представлением заданной формульной функции
является сеточным представлением заданной формульной функции 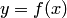 . Сеточная функция может задаваться совокупностью пар:
. Сеточная функция может задаваться совокупностью пар: 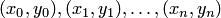 .
.
Требуется найти функцию 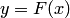 , принимающую в точках
, принимающую в точках 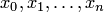 те же значения, что и функция
те же значения, что и функция 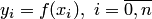 , то есть
, то есть 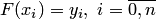 .
.
Точки 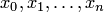 называются узлами интерполяции, а искомая функция
называются узлами интерполяции, а искомая функция 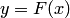 — интерполирующей.
— интерполирующей.
Геометрически это означает, что нужно найти кривую, проходящую через заданное множество точек 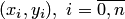 (рис. 4.2).
(рис. 4.2).
Одной из целей задачи интерполяции является вычисление значения функции в произвольной точке 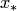 . При этом различаются собственно интерполирование, когда точка
. При этом различаются собственно интерполирование, когда точка 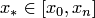 и экстраполирование, когда
и экстраполирование, когда 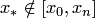 .
.
Заметим, что можно провести бесчисленное множество "плавных" кривых, проходящих через заданное множество точек. Поэтому задача интерполяции в общей постановке не имеет единственного решения.
Если в качестве интерполирующей функции выбрать алгебраический многочлен, степень которого связана с числом заданных узлов интерполяции (на единицу меньше), решение задачи является единственным. Покажем это. Воспользуемся сначала кусочным способом. Выделим из отрезка 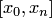 частичный отрезок [x_i,x_{i+k}] и рассмотрим сеточную функцию
частичный отрезок [x_i,x_{i+k}] и рассмотрим сеточную функцию 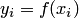 , заданную в (k+1)-м узле
, заданную в (k+1)-м узле 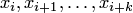 (узлы не совпадают):
(узлы не совпадают):
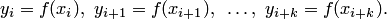
| (4.7) |
В качестве интерполирующей функции выберем алгебраический многочлен k-й степени (степень многочлена на единицу меньше количества узлов):
| (4.8) |
Будем искать неизвестные коэффициенты 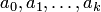 из условия интерполяции (4.3), т.е.
из условия интерполяции (4.3), т.е. 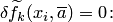
| (4.9) |
Теорема 4.1 (о единственности решения задачи интерполяции). Задача о нахождении интерполяционного многочлена 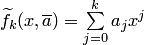 , удовлетворяющего условиям (4.9), на частичном отрезке
, удовлетворяющего условиям (4.9), на частичном отрезке 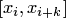 по заданной сеточной функции (4.7) имеет единственное решение.
по заданной сеточной функции (4.7) имеет единственное решение.
Доказательство. Запишем условия интерполяции (4.9) с учетом (4.8) и обозначения 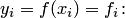
| (4.10) |
Эта система линейных алгебраических уравнений относительно коэффициентов 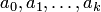 имеет единственное решение, так как определитель матрицы системы
имеет единственное решение, так как определитель матрицы системы
| (4.11) |
не равен нулю (доказательство последнего факта содержится в курсе линейной алгебры, где этот определитель называется определителем Вандермонда). Следовательно, задача интерполяции также имеет единственное решение.
Полагая 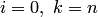 , приходим к глобальному способу решения поставленной задачи. А именно, если задана сеточная функция в (n+1)-м узле
, приходим к глобальному способу решения поставленной задачи. А именно, если задана сеточная функция в (n+1)-м узле 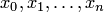 и требуется найти алгебраический многочлен с использованием условий интерполяции, то единственным решением задачи интерполяции является интерполяционный многочлен n-й степени:
и требуется найти алгебраический многочлен с использованием условий интерполяции, то единственным решением задачи интерполяции является интерполяционный многочлен n-й степени:
| (4.12) |
коэффициенты которого находятся из системы (4.10) при 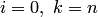 .
.
 2015-07-14
2015-07-14 424
424







