Возрастание и убывание функции

Возрастание и убывание дифференцируемой функции связано со знаком её производной. Напомним, что функция 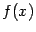называется возрастающей на интервале 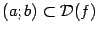, если для любых двух точек 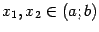из неравенства 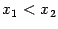следует, что 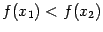; убывающей на интервале 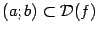, если из неравенства 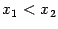следует, что 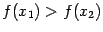; невозрастающей на интервале 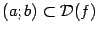, если из неравенства 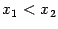следует, что 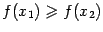, и неубывающей на интервале 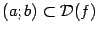, если из неравенства 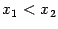следует, что .

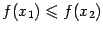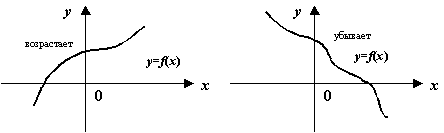
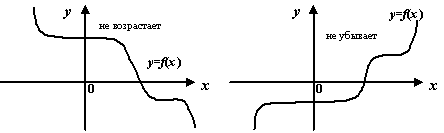
Рис.7.15.Графики возрастающей, убывающей, невозрастающей и неубывающей функций

Очевидно, что функция 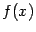возрастает тогда и только тогда, когда убывает функция 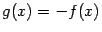; аналогичное утверждение связывает неубывающую функцию с невозрастающей.

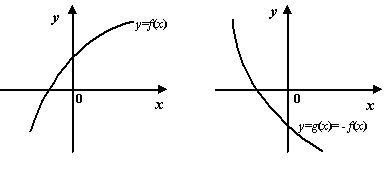
Рис.7.16.Графики функци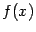й и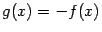

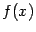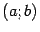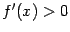Теорема 7.2 Пусть функция дифференцируема на интервале и при всех 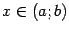. Тогда 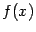возрастает на 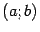. Если же 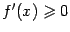при всех 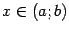, то 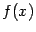не убывает на .

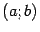Аналогично, если 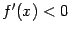при всех 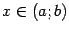, то 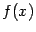убывает на 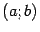, а если 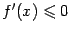при всех 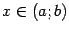, то 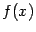не возрастает на .

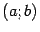Доказательство. В силу предыдущего замечания, теорему достаточно доказывать только для случаев 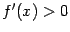и 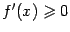. Пусть 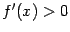при всех 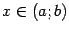и 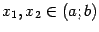, 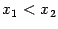. Применим к отрезку 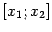формулу конечных приращений:

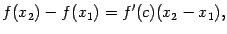
где 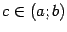. В правой част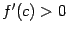и и 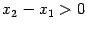, так что 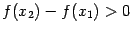, откуда 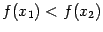, что означает возрастание функции.

Точно так же, если 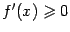, то получаем 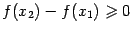, откуда 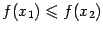, что означает неубывание функции.