Алгоритм выбора из пирамиды

Определение 1. Почти полным двоичным деревом будем называть двоичное дерево, для которого существует такое целое число h ≥ 0, что:

1. каждый лист дерева находится на уровне (h – 1) или h;

2. уровень (h – 1) максимально заполнен узлами;

3. все листья уровня h максимально смещены влево.

Определение 2. Будем называть пирамидой размера n почти полное двоичное дерево с n узлами, для которого содержимое каждого узла не больше содержимого отца этого узла.

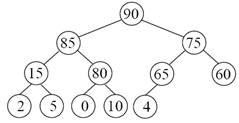
На рис. 3. приведён пример пирамиды размера 12, построенной из последовательности элементов 75, 80, 90, 5, 10, 4, 60, 2, 15, 0, 85, 65.

Определение 3. Кучей называется массив k из n элементов, для которого выполняются условия для всех 1 ≤ j < n. ()((1)/2)kjkj

Если пирамида реализуется с помощью массива, то такой массив является кучей. Элемент k (0) является корнем дерева. Отметим, что значение потомка в куче не превосходит значения предка. Таким образом, наибольший элемент дерева (или любого поддерева) находится в корневой вершине дерева (поддерева).

Движение по дереву осуществляется следующим образом:

1) предком элемента k (i) является k ([(i – 1)/2]);

2) левым сыном k (i) является k (2 i + 1);

3) правым сыном k (i) является k (2 i + 2).

В дереве, составляющем кучу, все уровни (кроме, может быть, последнего) заполнены полностью. Поэтому высота этого дерева равна O (log n), где n – число элементов в куче. Как будет показано ниже, количество основных операций над кучей пропорционально высоте дерева и, следовательно, составляет O (log n).

Алгоритм пирамидальной сортировки состоит из двух этапов:

 построение кучи из произвольного массива k;

 перестроение кучи и формирование отсортированного массива.

Рассмотрим первый этап, для чего создадим некоторую функцию, позволяющую сформировать кучу. Пусть её параметрами являются массив k и i – индекс элемента. Предположим, что поддеревья с корнями k (2 i + 1) и k (2 i + 2) удовлетворяют условиям кучи. Рассмотрим в качестве текущего элемента их отца k (i). Если для него свойство кучи не выполняется, то значение k (i) следует поменять со значением большего из его сыновей (например, с k (2 i + 1)). Теперь текущим узлом становится узел k (2 i + 1). Процесс формирования кучи продолжается до тех пор, пока значение текущего элемента меньше значения максимального из его сыновей и массив не закончится. Реализация восстановления свойства кучи с корнем в k (i) на примере целочисленного массива размера n представлена в листинге 2.