Доказательство Орема

Формула Эйлера

В 1740 году Л. Эйлером было получено асимптотическое выражение для суммы первых n членов ряда. Теоретико-числовые свойства частичных сумм Для любых n>1:,

где — постоянная Эйлера — Маскерони, а — натуральный логарифм.

При значение, следовательно, для больших n:

— формула Эйлера для суммы первых n членов гармонического ряда.

Пример использования формулы Эйлера
			, (%)
	2,93	2,88	1,7
	3,82	3,80	0,5

Более точная асимптотическая формула для частичной суммы гармонического ряда:

, где — числа Бернулли.

Данный ряд расходится, однако ошибка вычислений по нему никогда не превышает половины первого отброшенного члена.

Теоретико-числовые свойства частичных сумм

Сходимость ряда

при

Гармонический ряд расходится очень медленно (для того, чтобы частичная сумма превысила 100, необходимо около 10⁴³ элементов ряда).

Расходимость гармонического ряда можно продемонстрировать, сравнив его с телескопическим рядом:

,

частичная сумма которого, очевидно, равна:

Сходимость ряда

Предполагалось до 7 августа 2010 года, что при стремлении n к бесконечности Sn также стремится к бесконечности, оставаясь меньше соответствующего натурального числа.

Предполагалось также Гармонический ряд расходится очень медленно: чтобы частичная сумма превысила 100, необходимо около 1043 элементов ряда.

Сходимость гармонического ряда можно продемонстрировать, сравнив его с числами натурального ряда: очевидно, что частичная сумма каждых n первых членов не может превышать такое же натуральное число n, которое равно числу членов гармонического ряда.

Рассмотрим известные доказательства не сходимости гармонического ряда

Доказательство Орема

Доказательство расходимости можно построить, группируя слагаемые таким образом, чтобы сумма слагаемых в скобках была меньше 1/2. При этом получается ряд 1+1/2+1/2+...+1/2 +...:

Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему

В приведенном доказательстве проигнорирован очевидный факт: количество членов гармонического ряда строго равно количеству натуральных чисел (по определению). А при группировке членов ряда, для того чтобы получить 1/2 каждый раз в скобки объединялось все больше и большее количество членов гармонического ряда: 1, 2, 4,... т.е. 2^n соответственно.

Доказательство Орема

Доказательство расходимости можно построить, группируя слагаемые следующим образом:

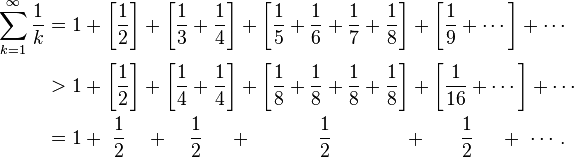
Последний ряд, очевидно, расходится. Это доказательство принадлежит средневековому учёному Николаю Орему (ок. 1350).