2015-08-13
577
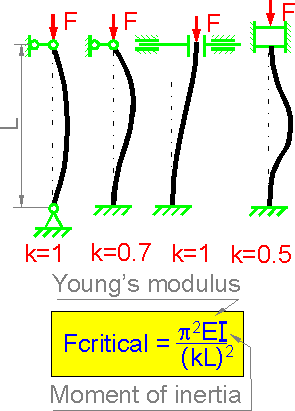
In 1757, Leonard Euler proposed a relationship for the critical load that would produce buckling in a pinned-pinned column. For other supporting schemes (fixed-pinned, fixed-fixed, fixed-free, etc.) engineers use an effective length Le = k*L where k is the effective length constant.
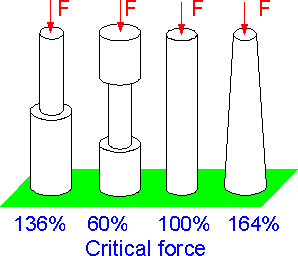The numbers show percents of critical buckling force for each column in comparison with the uniform column. The last case demonstrates the most efficient use of the material.
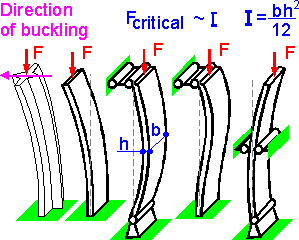There are two extreme directions with maximum and minimum values of the moment of inertia. The buckling occurs in the direction of the minimum moment of inertia.
For a rectangular section buckling occurs perpendicular to the longer side. The resulting deformed shape of the column depends on how the column is supported.
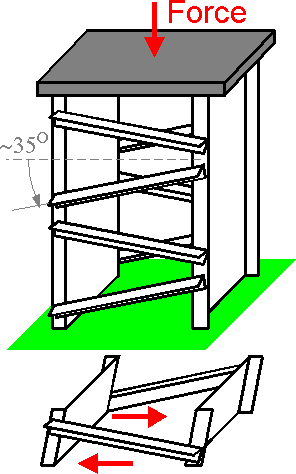The calculation shows that the critical force is the highest for a structure with maximum shear rigidity. This condition corresponds to an optimal angle 35.26 degrees. For smaller or larger angles the shear stiffness is smaller.
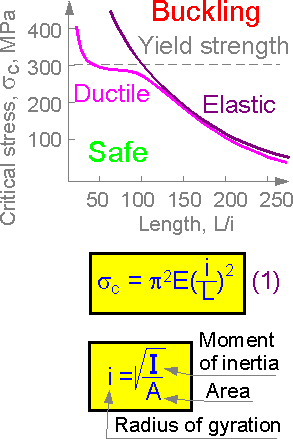The critical stress corresponding to buckling depends on beam length and yield properties of the material. In short columns the critical stress can exceed the yield strength (tension).
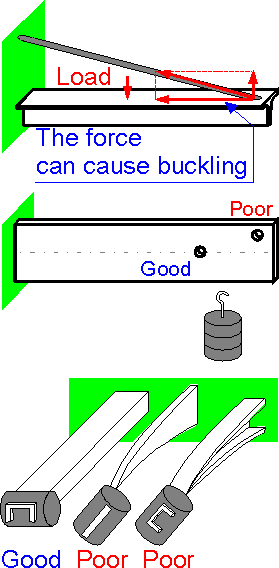A tensile force in the cable compresses the beam. The loading can result in buckling of the beam.
The closer to the fixed end, the smaller the bending moment. The closer to the neutral axis, the smaller the torque under buckling.
The first example of the cantilever beams demonstrates the most efficient use of the material. The last two structures are unstable due to possible buckling and torsion.
