2015-08-13
451
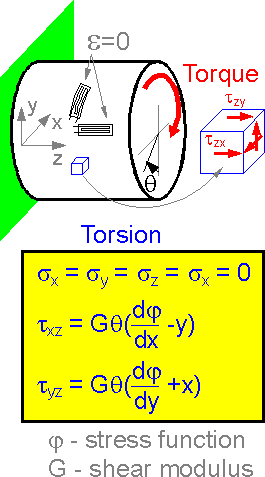
Torsion is related to shear stress. Only two shear stresses are nonzero at planes perpendicular to the shaft axis. All other stress components including all normal stresses in the chosen coordinate axes are equal to zero.
There is no tensile strain in the vertical or horizontal directions for pure shear (torsion). There are no readings on the two strain gauges shown.
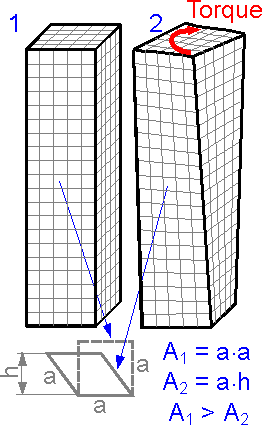The figure shows the results of a finite element analysis for a prismatic bar under torsion. The shear deformation is at a maximum in the center of the bar. The shape of the square mesh at the surface of the bar changes. The height of the rhombus and its area become smaller. This means that the bar becomes a little shorter.
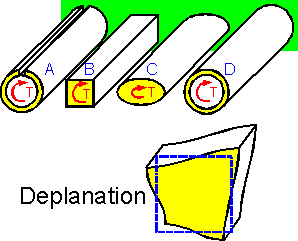The figure shows four specimens with equal cross sections. The thin-walled example A demonstrates the smallest torsional rigidity.
The specimens are shown in increasing order of the torsional rigidity.
Deplanation of a plane section is the out-of-plane deformation of its points. For all examples except cylinder D there is deplanation.
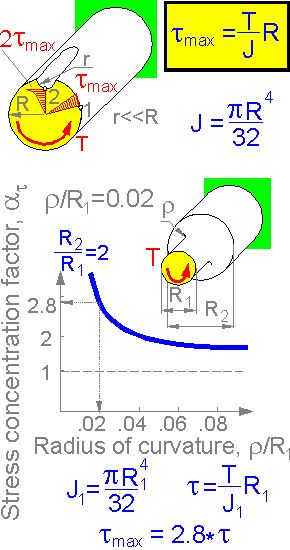Shear stress is doubled near the small keyslot. The stress concentration factor is equal to 2 for the small keyslot.
There is stress concentration near the diameter change. The stress concentration factor depends on radius of curvature.
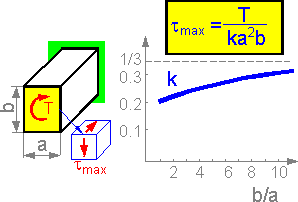The formula defines maximum shear stress for a rectangular section. The maximum shear stress acts at the middle of the longer edge of the rectangle. The coefficient k grows from 0.208 at b/a=1 to 0.333 at infinity.
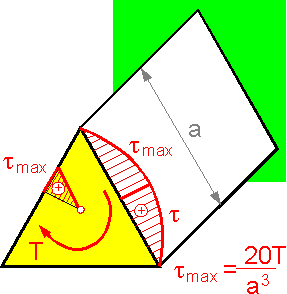Maximum shear stress in the middle of a side of a triangle is inversely proportional to a3. The shear stress is equal to zero in the corners and center.
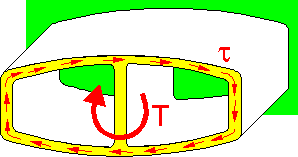For thin-walled symetrical sections the shear stress is approximately zero in the inner wall. All shear stresses tend toward the "external circle".
