If there are a number of possible messages, then each one can be expected to occur a certain fraction of the time. This fraction is called the probability of the message. For example, if an ordinary coin is tossed, the two outcomes, heads or tails, will each occur with probability ½. Similarly, if a card is selected at random from a 52-card deck, each of the four suits will occur with probability ¼.
Shannon determined that the information content of a message is inversely related to its probability of occurrence. The more unlikely a message is, the more information it contains. Based on this concept, the exact information value of a message can be determined mathematically. If the probability of a given outcome is denoted by p, then Shannon defined the information content (I) of that message, measured in bits, to be equal to the base 2 logarithm (log2) of the reciprocal of p. (The log2 of a given number is the exponent that must be given to the number 2 in order to obtain the given number. Log 2 of 8 = 3, for example, because 23 = 8.) The relation between information content and probability can be represented by the equation I = log21/ p
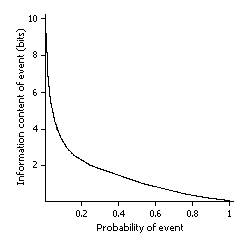
The graph below illustrates a plot of this function. The horizontal axis shows the probability p; p is a number between 0 (an impossible event) and 1 (a certain event). The vertical axis shows the information content.
|
As can be seen in the graph, the less likely or probable an event, the more information it conveys. Here is a short table giving several values of p and the corresponding information content I:

|
The more possibilities a source contains, the more information it contains and, therefore, the more bits needed to represent the information content. For example, if a card is picked at random from a 52-card deck and the exact value of the card is to be communicated, then each possibility has probability 1/52. According to the formula I = log21/ p, each possible outcome has an information content equal to log252, which equals 5.70044.
 2015-08-21
2015-08-21 492
492








