2015-08-21
656
Метод проектирования модифицированных сетей Хопфилда описан в работе [25],
на основе этого метода разработан алгоритм синтеза, который реализован в ППП NT
в виде подфункции solvehop2(t) М-функции newhop.
Если задано множество целевых точек равновесия, представленных матрицей T, то функция newhop возвращает матрицу весов и вектор смещений для рекуррентного слоя сети Хопфилда. При этом гарантируется, что точки устойчивого равновесия будут соответствовать целевым векторам, но могут появиться и так называемые паразитные точки.
В процессе синтеза сети число таких нежелательных точек сводится к минимуму.
Пусть задано Q целевых векторов, образующих матрицу T размера S ´ Q:
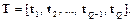(8.5)
Образуем новую матрицу Y размера S ´ Q –1 следующего вида:
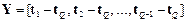(8.6)
Вычислим разложение матрицы Y по сингулярным числам:
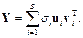(8.7)
Далее образуем матрицы
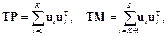(8.8)
где K – ранг матрицы Y.
Построим динамическую систему
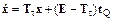, (8.9)
где T t – матрица вида ТР – tТМ; t – динамический параметр (в алгоритме принят равным 10); E – единичная матрица.
|
|
|
Вычислим дискретную модель для системы (8.9):
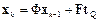, (8.10)
где Ф – переходная матрица вида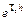 
; F – матрица передачи входа вида 
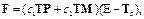с1 = e h –1, c2 = (1–e –th)/t; h – такт дискретности (в алгоритме принят равным 0.15 c).
Соответствующая матрица весов рекуррентного слоя и вектор смещения вычисляются следующим образом:
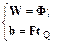(8.11)
Когда сеть спроектирована, она может быть проверена с одним или большим числом векторов входа. Весьма вероятно, что векторы входа, близкие к целевым точкам, равновесия найдут свои цели. Способность модифицированной сети Хопфилда быстро обрабатывать наборы векторов входа позволяет проверить сеть за относительно короткое время. Сначала можно проверить, что точки равновесия целевых векторов действительно принадлежат вершинам гиперкуба, а затем можно определить области притяжения этих точек и обнаружить паразитные точки равновесия, если они имеются.
Рассмотрим следующий пример. Предположим, что требуется создать модифицированную сеть Хопфилда с двумя точками равновесия, заданными в трехмерном пространстве:
T = [–1 –1 1; 1 –1 1]'
T =
–1 1
–1 –1
1 1
Выполним синтез сети, используя М-функцию newhop:
net = newhop(T);
Удостоверимся, что разработанная сеть имеет устойчивые состояния в этих двух точках. Выполним моделирование сети Хопфилда, приняв во внимание, что эта сеть не имеет входов
и содержит рекуррентный слой; в этом случае целевые векторы определяют начальное состояние слоя Ai, а второй аргумент функции sim определяется числом целевых векторов:
Ai = T;
[Y,Pf,Af] = sim(net,2,[],Ai);
Y
Y =
–1 1
–1 –1
1 1
Действительно, устойчивые положения равновесия сети находятся в назначенных точках.
|
|
|
Зададим другое начальное условие в виде массива ячеек:
Ai = {[–0.9; –0.8; 0.7]};
Ai{1,1}
ans =
–0.9000
–0.8000
0.7000
Эта точка расположена вблизи первого положения равновесия, так что можно ожидать, что сеть будет сходиться именно к этой точке. При таком способе вызова функции sim в качестве второго параметра указываются такт дискретности и количество шагов моделирования:
[Y,Pf,Af] = sim(net,{1 5},{},Ai);
Y{1}
Y =
–1
–1
Действительно, из заданного начального состояния сеть вернулась в устойчивое положение равновесия. Желательно, чтобы сеть вела себя аналогичным образом при задании любой начальной точки в пределах куба, вершины которого составлены изо всех комбинаций чисел 1 и –1 в трехмерном пространстве. К сожалению, этого нельзя гарантировать, и достаточно часто сети Хопфилда включают нежелательные паразитные точки равновесия.
Пример:
Рассмотрим сеть Хопфилда с четырьмя нейронами и определим 4 точки равновесия
в виде следующего массива целевых векторов:
T = [1 –1; –1 1; 1 1; –1 –1]'
T =
1 –1 1 –1
–1 1 1 –1
На рис. 8.7 показаны эти 4 точки равновесия на плоскости состояний сети Хопфилда.
plot(T(1,:), T(2,:),'*r') % Рис.8.7
axis([–1.1 1.1 –1.1 1.1])
title('Точки равновесия сети Хопфилда')
xlabel('a(1)'), ylabel('a(2)')
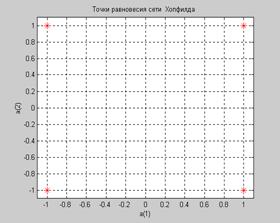Рис. 8.7
Рассчитаем веса и смещения модифицированной сети Хопфилда, использую М-функцию newhop:
net = newhop(T);
W= net.LW{1,1}
b = net.b{1,1}
W =
1.1618 0
0 1.1618
b =
3.5934e–017
3.5934e–017
Проверим, принадлежат ли вершины квадрата к сети Хопфилда:
Ai = T;
[Y,Pf,Af] = sim(net,4,[],Ai)
Y =
1 –1 1 –1
–1 1 1 –1
Pf = []
Af =
1 –1 1 –1
–1 1 1 –1
Как и следовало ожидать, выходы сети равны целевым векторам.
Теперь проверим поведение сети при случайных начальных условиях:
plot(T(1,:), T(2,:),'*r'), hold on
axis([–1.1 1.1 –1.1 1.1])
xlabel('a(1)'), ylabel('a(2)')
new = newhop(T);
[Y,Pf,Af] = sim(net,4,[],T);
for i =1:25
a = {rands(2,1)};
[Y,Pf,Af] = sim(net,{1,20},{},a);
record = [cell2mat(a) cell2mat(Y)];
start = cell2mat(a);
plot(start(1,1), start(2,1), 'kx', record(1,:), record(2,:))
end
Результат представлен на рис. 8.8.
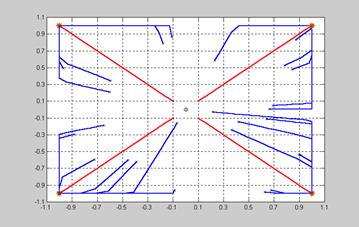Рис. 8.8
Читатель может продолжить изучение модифицированных сетей Хопфилда, обратившись к демонстрационным примерам. Пример двумерной сети можно найти в демонстрации demohop1, пример неустойчивой точки равновесия – в демонстрации demohop2.
Демонстрация demohop3 дает пример трехмерной модифицированной сети Хопфилда. Демонстрация demohop4 иллюстрирует появление устойчивых паразитных точек равновесия.
