2015-08-21
376
В целом ряде экспериментов на токамаках оказывается, что зависимости от малого радиуса температуры и плотности оказываются подобными, то есть температура пропорциональна некоторой степени плотности. Возможно, что это явление связано с температурно-дрейфовой неустойчивостью.
Эту неустойчивость следует рассматривать в двухжидкостной модели. Будем считать, что характерная частота неустойчивости много меньше электронной ленгмюровской частоты,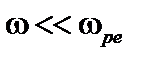 
. В этом случае можно пренебречь инерцией электронов. Будем предполагать также, что продольная теплопроводность достаточно высока, и как ионная, так и электронная температуры вдоль силовой линии не меняются, 
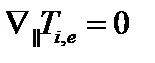. В этом приближении уравнение импульса для электронов упрощается, 
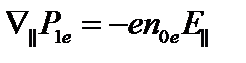, или в фурье-представлении
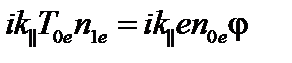. (3.6.1)
Здесь мы положили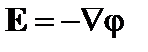 
. Положим также, что невозмущённая плазма квазинейтральна, 
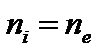. Отсюда мы легко получаем, что электроны распределены по Больцману:
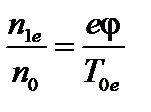. (3.6.2)
При рассмотрении ионов будем полагать, что поперечная длина волны много больше ионного ларморовского радиуса,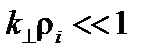 
. Кроме того, положим 
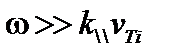. Это позволяет пользоваться МГД-уравнениями, то есть затуханием Ландау можно пренебречь.
Уравнение непрерывности в фурье-представлении дает
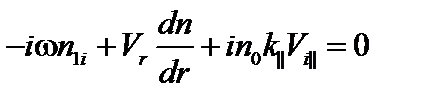. (3.6.3)
Параллельная составляющая уравнения импульса имеет вид:
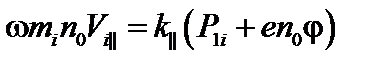. (3.6.4)
Вместо уравнения энергии, пренебрегая теплообменом, воспользуемся уравнением адиабаты. При этом показатель адиабаты положим равным 5/3:
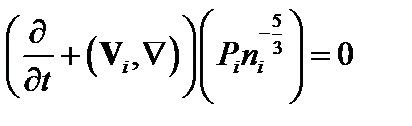. (3.6.5)
Будем считать, что скорость ионов определяется дрейфом в электрическом поле.
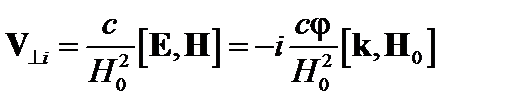. (3.6.6)
Линеаризуем уравнение (3.6.6). Все величины в первой скобке – первого порядка малости. Поэтому произведение во второй скобке можно вычислить в нулевом приближении: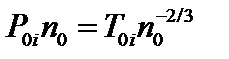 
. В нулевом приближении все величины зависят только от радиуса, поэтому 
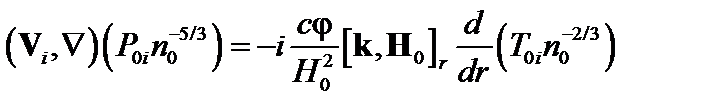. Наиболее опасны возмущения, вытянутые вдоль силовых линий. Поэтому будем считать, что 
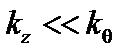. Имея в виду, что 
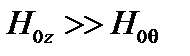, окончательно получаем
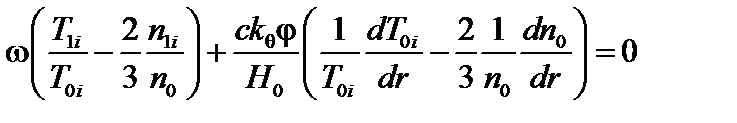. (3.6.7)
Введем дрейфовые частоты
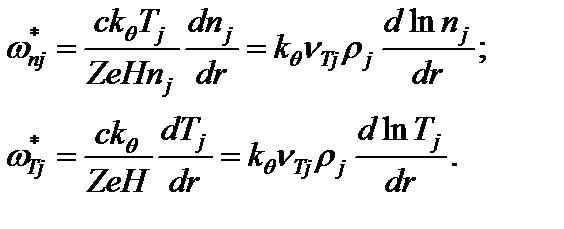Размер (3.6.8)
Здесь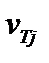 
– тепловая скорость, 
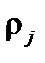– ларморовский радиус. Для электронов 
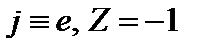. Для ионов 
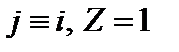. Введем также величинуη j:
; 
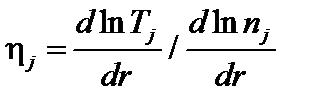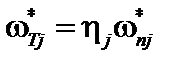. (3.6.9)
Уравнение ((3.6.7) теперь перепишется так:
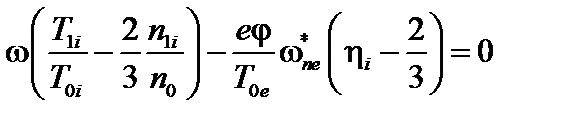. (3.6.9)
Необходимо учесть также условие квазинейтральности
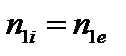. (3.6.10)
Система уравнений (3.6.2)–(3.6.4) и (3.6.10) имеет решение в том и только в том случае, если её определитель обращается в ноль, то есть
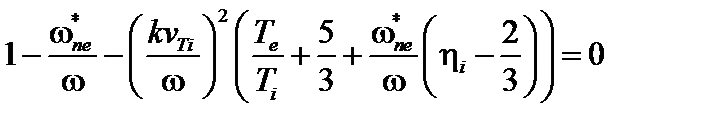. (3.6.11)
Рассмотрим случай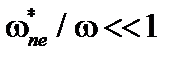 
. Дисперсионное уравнение приобретает вид: 
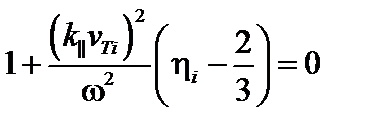или
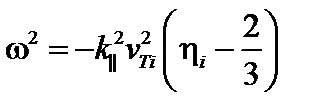. (3.6.12)
Условие устойчивости имеет вид
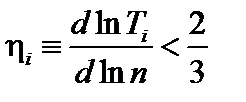. (3.6.13)
Это означает, что температура от периферии к центру не должна нарастать слишком быстро по сравнению с плотностью.
В реальном токамаке вследствие ненулевого шира при удалении от рациональной поверхности нарастает величина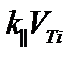 
и становится порядка 
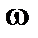. В этом случае необходимо кинетическое рассмотрение. Оно даёт следующее условие устойчивости:
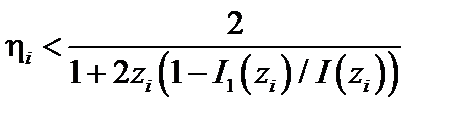. (3.6.14)
Здесь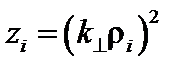 
, I0 и I1 – модифицированные функции Бесселя.
В случае длинноволновых (в перпендикулярном магнитному полю направлении) волн, то есть для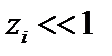 
это условие упрощается:
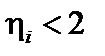. (3.6.15)
Заметим, что при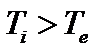 
мода становится более устойчивой, чем в обратном случае. Этот факт был сначала обнаружен экспериментально на установке TFTR, на которой в результате нейтральной инжекции ионная температура впервые превзошла электронную. При этом формально критерий устойчивости, полученный ранее для 
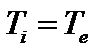, был нарушен, а неустойчивость не наблюдалась. И лишь позднее этот эффект был объяснен теоретически О.П. Погуце c сотрудниками.
