Принцип аргумента

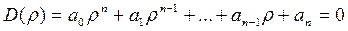
По теореме Виета хар-ий полином может быть выражен через корни этого полинома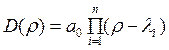

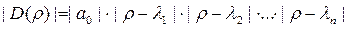
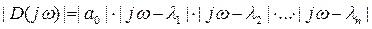
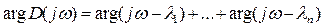
Для частотной характеристики вместо 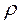полагается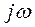

,

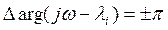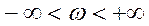
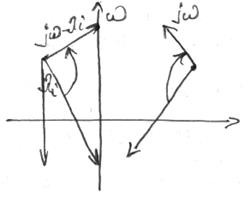
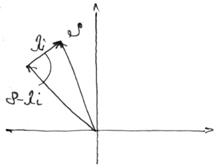
Приращение аргумента – это на какой угол повернется вектор. Он повернется на 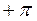или 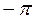в зависимости от того, в какой полуплоскости находятся корни 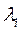, если в левой, то против часовой стрелки, если в правой – наоборот.

Характеристический полином – это произведение таких векторов.

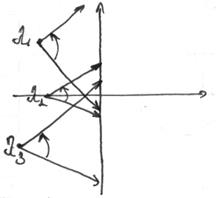Если все корни хар-го уравнения находятся в левой полуплоскости, то приращение аргумента находится: ,

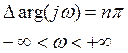n – порядок полинома.

Если хар-ий полином имеет m корней в правой полуплоскости, то значит он имеет n-m корней в левой полуплоскости, тогда приращение аргумента:

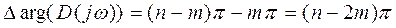, (можно поделить на пи, сократить).

Другой принцип аргумента: приращение аргумента хар-го полинома, при изменении частоты от 0 до 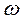равно:

;

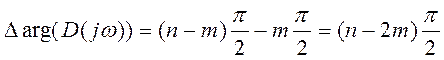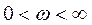
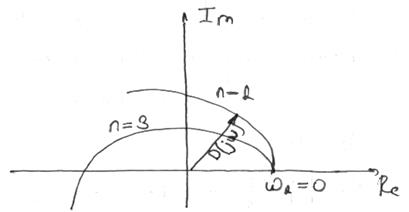
Для устойчивости системы n -го порядка вектор 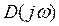должен повернуться против часовой стрелки на 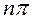, т.е. последовательно пройти n квадрантов.

Если же по отдельности рисовать действительную и мнимую хар-ки, то поочередное прохождении квадрантов эквивалентно:

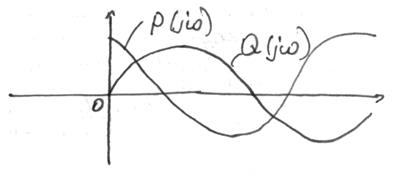
Из принципа аргумента следует критерий устойчивости Михайлова. В самом деле – система устойчива только если корни знаменателя передаточной функции находятся в отрицательной полуплоскости. А для этого нужно, чтобы приращение аргумента составило np. Итого получаем: если нули действительной и мнимой части знаменателя передаточной функции D(jw) при w от 0 до 00 чередуются между собой то система усточнива иначе не устойчива. Или же в другой форме - если годограф знаменателя проходит через n квадрантов, то система устойчива(квадрат область на комплексной плоскости где знак действительной и мнимой части определён. Всего квадрантов 4) – при этом приращение аргумента составит np/2, а это значит, что при частоте от -00 до 00 приращение аргументов составило бы np.

Пример. Пусть W(s)=k/(s*(T²s²+2xTs+1)

T=0,01 c.

x=0,05

k=5 (первый вариант) k=20 - 2-й вариант.

Расчитаем передаточную функцию замкнутой системы c отрицательной единичной обратной связью. Получим

Ф(S)=W(s)/(1+W(s)) (6.1)

Подставив W(s) имеем

Ф(S)=k/(T²s³+2xTs²+s+k) (6.2)

Заменив S на jw получаем что знаменатель передаточной функции равен

D(jw)= T²(jw)³+2xT(jw)²+jw+k (6.3)

Разделим знаменатель на дейстительную часть U(w) и мнимую jV(w) тогда

U(w)=k-2xTw² (6.4.1)

V(w)= w-T²w³ (6.4.2)

Имеем корни w₁=0 w₂=±100 для обоих вариантов

Другие два корня равны w_3,4=± 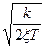(6.5)

Для первого варианта это ±50 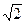т.е. приблизительно ±70. Как видим, действительная и мнимая часть обращаются в 0 попеременно - система устойчива. Для второго же варианта получим корни ±100 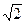или ±141 - тут корни обращаются в 0 не попеременно, значит система неустойчиво (Задание - самостоятельно построить годограф системы и показать, что в первом случае он проходит через 4 квадранта последовательно, а во втором - нет)