При моделировании случайных величин

Число испытаний N определяет точность получаемых результа­тов моделирования. Если необходимо оценить величину параметра а по результатам моделирования 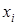, то за оценку следует брать величи­ну 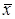, которая выступает в функции от .

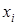Из-за случайности 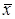будет отличаться от а, то есть

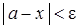(3.16)

где e – точность оценки. Вероятность того, что данное неравенство выполняется, обозначим через a:

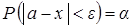(3.17)

Для определения точности результатов статистических испыта­ний необходимо воспользоваться выражением (3.17).

Определение количества реализаций для оценки вероятно­сти наступления события. Пусть целью моделирования будет опре­деление вероятности наступления некоторого события А, опреде­ляющего состояние моделированной системы. В любой из N реализа­ций процесс наступления события А является случайной величиной, которая может приобретать значение 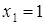с вероятностью р и 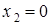с вероятностью 1– р. Тогда можно найти математическое ожидание

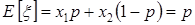(3.18) и дисперсию

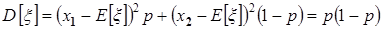(3.19)

В качестве оценки р используют частоту наступления собы­тия A. Эта оценка несмещенная, состоятельная и эффективная.

При условии, что N заведомо задано, достаточно накапливать т:

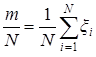, (3.20)

где 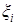– наступление события A в реализации, 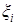={1,0}. По формулам (3.18-3.20) находим

.

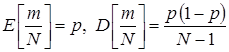В соответствии с центральной предельной теоремой (в данном случае можно взять теорему Лапласа) случайная величина – будет иметь распределение, близкое к нормальному (рис. 3.13). Поэтому для каждой достоверности a из таблиц нормального распределения можно найти такую величину 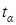, что точность e будет равняться ве­личине

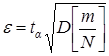(3.21)

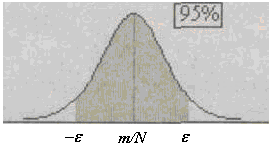
Рис. 3.13

При a =0,95 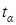= 1,96.

При a =0,997 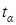=3.

Подставим в уравнение (3.21) выражение дисперсии

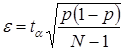. (3.22)

Отсюда находим

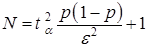. (3.23)

Поскольку вероятность р заранее неизвестна, прибегают к проб­ным испытаниям (N = 50... 100), получают частоту 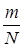и подставляют ее значения в выражение (3.23) вместо р, после чего определяют ко­нечное количество испытаний.

Определение количества реализаций для оценки среднего значения случайной величины. Пусть случайная величина имеет математическое ожидание а и дисперсию s². В реализации с номером i она принимает значение 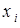. Для оценки математического ожидания а используем среднее

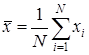(3.24)

В соответствии с центральной предельной теоремой при боль­ших значениях N среднее арифметическое 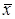будет нормально рас­пределено с математическим ожиданием а и дисперсией 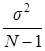. Тогда

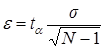(3.25)

Отсюда

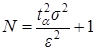(3.26)

Поскольку дисперсия оцениваемой случайной величины неиз­вестна, необходимо провести 50-100 испытаний и оценить 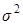, а по­том полученное значение оценки подставить в формулу (3.26), чтобы определить необходимое количество реализаций N.